Concavity and the Second Derivative Test

If $y = f(x)$ is a function, the second derivative of y (or of f) is the derivative of the first derivative. Notation:

$$\dfrac{d^2 y}{dx^2}, \quad \dfrac{d^2 f}{dx^2}, \quad y'', \quad f''.$$

Thus,

$$\dfrac{d^2 y}{dx^2} = \der {} x \left(\der y x\right).$$

Example. Find the second derivatives of the following functions.

(a) $y = x^2$ .

(b) $y = \dfrac{1}{x^2}$ .

(c) $y = \dfrac{1}{6}x^3 - 2 x^2 + 5 x + 4$ .

(a)

$$y' = 2 x, \quad y'' = 2.\quad\halmos$$

(b)

$$y' = -\dfrac{2}{x^3}, \quad y'' = \dfrac{6}{x^4}.\quad\halmos$$

(c)

$$y' = \dfrac{1}{2}x^2 - 4 x + 5, \quad y'' = x - 4.\quad\halmos$$

The first derivative gives information about whether a function increases or decreases. In fact:

(a) A differentiable function increases on intervals where its derivative is positive, and vice versa.

(b) A differentiable function decreases on intervals where its derivative is negative, and vice versa.

A function $y = f(x)$ is concave up on an open interval if $y''$ is positive on the interval. And a function $y = f(x)$ is concave down on an open interval if $y''$ is negative on the interval.

A point where the concavity goes from up to down or from down to up is called an inflection point.

What do these conditions mean geometrically?

Consider the curve below.

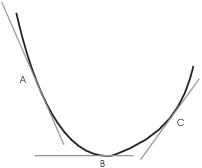
$$\hbox{\epsfysize=1.5in \epsffile{concavity-1.eps}}$$

The tangent line A has negative slope, the tangent line B has zero slope, and the tangent line C has positive slope. Therefore, as you move from left to right, the slope of the tangent line increases.

But the slope of the tangent line is given by $y'$ , and to say something increases means its derivative is positive. So the derivative of $y'$ --- which is $y''$ --- must be positive. By the definition, this means the curve is concave up.

Now consider the curve below.

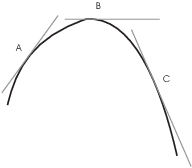
$$\hbox{\epsfysize=1.5in \epsffile{concavity-2.eps}}$$

The tangent line at A has positive slope, the tangent line at B has zero slope, and the tangent line at C has negative slope. As you move from left to right, the slope of the tangent line decreases.

The slope of the tangent line is given by $y'$ , and to say something decreases means its derivative is negative. So the derivative of $y'$ --- which is $y''$ --- must be negative. By the definition, this means the curve is concave down.

The two pictures exemplify the geometric meanings of concave up and concave down.

Example. The graph of a function is pictured below.

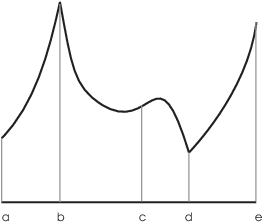
$$\hbox{\epsfysize=2in \epsffile{concavity-3.eps}}$$

Determine the intervals on which the function is concave up and the intervals on which it is concave down. Find the x-coordinates of any inflection points.

The graph is concave up on $a < x < b$ , $b < x < c$ , and $d < x < e$ . The graph is concave down on $c < x < d$ .

Note that concavity is a property of a graph on an open interval, so the endpoints aren't included.

There are inflection points at $x = c$ and at $x = d$ .

Example. Find the intervals on which $y = \dfrac{1}{4}x^4 + \dfrac{1}{2}x^3 - 3 x^2 + 6$ is concave up and the intervals on which it is concave down. Find the x-coordinates of any inflection points.

$$y' = x^3 + \dfrac{3}{2}x^2 - 6 x, \quad y'' = 3 x^2 - 3 x - 6 = 3(x^2 - x - 2) = 3(x - 2)(x + 1).$$

I set up a sign chart for $y''$ , just as I use a sign chart for $y'$ to tell where a function increases and where it decreases. The break points for my concavity sign chart will be the x-values where $y'' = 0$ and the x-values where $y''$ is undefined.

In this case, $y'' = 0$ for $x = 2$ and $x = -1$ , and there are no points where $y''$ is undefined. The break points are at $x = 2$ and $x = -1$ .

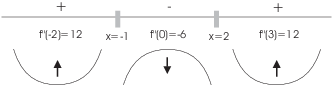
$$\hbox{\epsfxsize=3in \epsffile{concavity-4.eps}}$$

I picked numbers in each interval and plugged the numbers into $y''$ . If $y''$ is positive, I put a "+" on the interval and draw a concave-up curve below the interval; if $y''$ is negative, I put a "-" on the interval and draw a concave-down curve below the interval.

The function is concave up for $x < -1$ and for $x > 2$ . It is concave down for $-1 < x < 2$ . $x = -1$ and $x = 2$ are inflection points.

Example. Find the intervals on which $y = \dfrac{9}{4}x^{4/3} - 9 x^{1/3}$ is concave up and the intervals on which it is concave down. Find the x-coordinates of any inflection points.

$$y' = 3 x^{1/3} - 3 x^{-2/3}, \quad y'' = x^{-2/3} + 2 x^{-5/3} = \dfrac{x + 2}{x^{5/3}}.$$

$y'' = 0$ for $x = -2$ ; $y''$ is undefined for $x = 0$ .

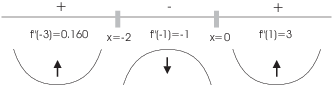
$$\hbox{\epsfxsize=3in \epsffile{concavity-5.eps}}$$

The function is concave up for $x < -2$ and for $x > 0$ . It is concave down for $-2 < x < 0$ . $x = -2$ and $x = 0$ are inflection points.

Concavity provides way to tell whether a critical point is a max or a min --- well, sometimes. This method is called the Second Derivative Test.

Consider a critical point where $y' = 0$ , i.e. where the tangent line is horizontal. Here are two possibilities.

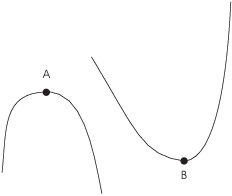
$$\hbox{\epsfysize=1.75in \epsffile{concavity-6.eps}}$$

The point A is a local max; it occurs at a place where the curve is concave down, i.e. where $y'' < 0$ .

The point B is a local min; it occurs at a place where the curve is concave up, i.e. where $y'' > 0$ .

Theorem. Suppose $f''$ is defined on an open interval, and for some point c in the interval $f'(c) = 0$ . Then:

(a) If $f''(c) < 0$ , then $x = c$ is a local max.

(b) If $f''(c) > 0$ , then $x = c$ is a local min.

(c) If $f''(c) = 0$ , the test fails. Try the First Derivative Test.

Example. Use the Second Derivative Test to classify the critical points of $y = \dfrac{1}{4}x^4 - 2 x^3 + 6$ .

$$y' = x^3 - 6 x^2 = x^2(x - 6), \quad y'' = 3 x^2 - 12 x.$$

The critical points are $x = 0$ and $x = 6$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & x & & $y'' = 3 x^2 - 12 x$ & & Result & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 6 & & $36 > 0$ & & min & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 0 & & 0 & & Test fails & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Here's the graph:

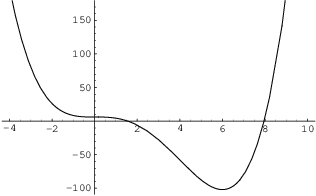
$$\hbox{\epsfysize=1.75in \epsffile{concavity-7.eps}}$$

In fact, $x = 0$ is neither a max nor a min.

Remark. It is not true that if $f'(c) = 0$ (so c is a critical point) and $f''(c) = 0$ (so the Second Derivative Test fails), then $x = c$ is neither a max nor a min. To say the test fails means that you can draw no conclusion, and you need to do more work. The point could still be a max or a min!

For example, consider $y = x^4$ . Then $y' = 4 x^3$ and $y'' = 12 x^2$ , so $y'(0) = 0$ and $y''(0) = 0$ . Thus, $x = 0$ is a critical point, and the Second Derivative Test fails. Nevertheless, $x = 0$ is a local min, as you can verify by using the First Derivative Test.

This example also shows that if $y''(c)= 0$ , it does not mean that c is an inflection point. In fact, the graph of $y = x^4$ is always concave up, so the concavity does not change at $x = 0$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga