We've seen that we can approximate the area under a curve by
using a sum of rectangle areas. But suppose I'm trying to find the
exact area under a curve --- say ![]() from
from ![]() to
to ![]() . Since increasing the number of rectangles increases
the accuracy of the approximation, maybe I'd get the exact area if I
could use an "infinite number of rectangles". I will give a
rough description of how we might do this.
. Since increasing the number of rectangles increases
the accuracy of the approximation, maybe I'd get the exact area if I
could use an "infinite number of rectangles". I will give a
rough description of how we might do this.
To do this, I start by breaking the interval ![]() up into n subintervals of lengths
up into n subintervals of lengths ![]() ,
, ![]() , ...,
, ..., ![]() . In the k-th subinterval, I pick some point
. In the k-th subinterval, I pick some point ![]() , and use
, and use ![]() as the height of
the k-th rectangle.
as the height of
the k-th rectangle.
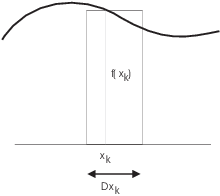
The sum of the areas of the rectangles approximates the area under the curve:
![]()
The more rectangles I take, the better the approximation. So it's reasonable to suppose that the exact area would be given by the limit of such sums, as n goes to infinity:
![]()
The expression on the right --- a limit of a sum, or a Riemann sum --- is called the
definite integral of ![]() from a to b and is denoted as
follows:
from a to b and is denoted as
follows:
![]()
If the limit of the sum on the right side is defined, the function f
is integrable on the interval ![]() .
.
Remark. In the definition above, I'm passing over a number of technical points for the sake of getting the intuitive idea across. For example, what does it mean to let the number of rectangles become infinite? Does it matter how the rectangles' widths or the evaluation points are chosen?
A careful treatment of the Riemann integral has to take these considerations into account.
It is possible to compute areas using the formula above, though it's not easy. Here's an example of a direct computation using the defintion.
Example. Use the limit of a sum to compute the
area under ![]() from
from ![]() to
to ![]() --- that is, the definite integral
--- that is, the definite integral
![]()
I will need the following summation formulas:
![]()
Divide up the interval ![]() into n equal subintervals.
Each has length
into n equal subintervals.
Each has length ![]() . I'll evaluate the
function at the right-hand endpoints. These are
. I'll evaluate the
function at the right-hand endpoints. These are
![]()
The k-th point is ![]() , so the height of the
k-th rectangle is
, so the height of the
k-th rectangle is
![]()
The sum of the rectangles' areas is
![]()
Applying the sum formulas above, I get
![]()
The (exact) area is
![]()
While this approach works, it's pretty complicated! I'll discuss better ways to compute definite integrals shortly.
Not all functions are integrable. The following result which I'll state without proof covers most of the cases we'll need:
Theorem. A bounded function with finitely many
discontinuities is integrable.![]()
For example, consider the function
![]()
There is a single discontinuity at ![]() . Hence, f is integrable on any interval.
. Hence, f is integrable on any interval.
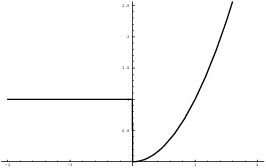
In particular, a continuous function is integrable.
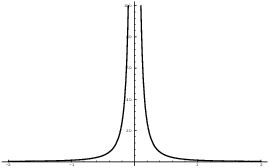
On the other hand, ![]() is not bounded
near
is not bounded
near ![]() , so it is not integrable on any interval
containing 0.
, so it is not integrable on any interval
containing 0.
In some cases, you can use the fact that the definite integral represents the area under a curve to evaluate the integral geometrically.
Example. Compute ![]() .
.
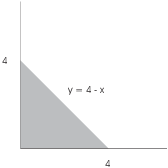
The integral represents the area of a triangle with height 4 and base 4, so
![]()
Example. Compute ![]() .
.
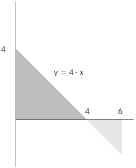
The area consists of the piece in the last problem, together with a piece of area 2. But the second piece is below the x-axis, so it is taken as negative in the definite integral:
![]()
Example. Compute ![]() .
.
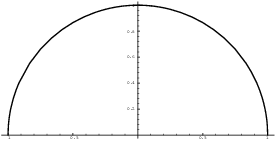
This is half the area of a circle of radius 1:
![]()
Here are some properties of definite integrals. I'll present them without proofs.
1. If k is a number, then
![]()
This is another way of saying that the area of a rectangle is the base times the height.

Example. Compute ![]() .
.
![]()
2.
![]()
This says that the integral of a sum is the sum of the integrals.
3. If ![]() for
for ![]() , then
, then
![]()
This says that bigger functions have bigger integrals.
Example. Use the inequality ![]() to estimate
to estimate ![]() .
.
![]()
4.
![]()
That is, switching the limits of integration multiplies the integral by -1.
As a special case,
![]()
5.
![]()
That is, integrating from a to b and then from b to c is the same as integrating all the way from a to c:
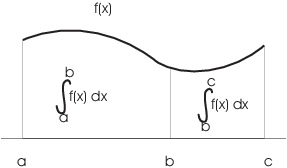
Example. Simplify ![]() .
.
![]()
6. ( The Mean Value Theorem for Integrals)
There is a number c, ![]() , such that
, such that
![]()
![]() represents the height of a rectangle on the integral
represents the height of a rectangle on the integral
![]() which has the same area as the area under the curve.
which has the same area as the area under the curve.

Example. Use the Mean Value Theorem for
Integrals to estimate ![]() .
.
Applying the Mean Value Theorem for Integrals, I find that there is a number c between 0 and 2 such that
![]()
Now
![]()
Therefore,
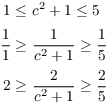
So
![]()
Copyright 2018 by Bruce Ikenaga