Differentials

Calculus is over three hundred years old, but the modern approach via limits only dates to the early 1800's with Cauchy. Historically, the use of differentials antedates the "rigorous approach" we now take to the derivative.

For example, Carl Boyer [1] notes:

"Increments and decrements, rather than rates of change, were the fundamental elements in the work leading to that of Leibniz, and played a larger part in the calculus of Newton than is usually recognized. The differential became the primary notion, and it was not effectively displaced as such until Cauchy, in the nineteenth century, made the derivative the basic concept."

A differential was regarded loosely as an infinitely small nonzero quantity. For example, here is a computation of the derivative of $x^2$ via differentials. Increment x by an infinitely small amount $dx$ , which produces an infinitely small change $dy$ in $y = x^2$ . This change is

$$dy = (x + dx)^2 - x^2 = x^2 + 2 x\,dx + (dx)^2 - x^2 = 2 x\,dx + (dx)^2.$$

Divide through by $dx$ :

$$\der y x = 2 x + dx.$$

Since $dx$ is "infinitely small", I may neglect it:

$$\der y x = 2 x.$$

This approach came to be regarded as imprecise. What does it mean for something to be "infinitely small"? How can something be "infinitely small", but not 0? What can you "neglect"?

Eventually, infinitely small quantities --- infinitesimals --- as well as infinitely large quantities were rehabilitated in the work of the American logician Abraham Robinson. Though calculus can be done using infinitesimals, it is standard practice to use limits and difference quotients instead.

The approach developed by Cauchy, which is more or less the approach that I'll use, makes no reference to "infinitely small" quantities. The definition of the derivative is:

$$\der y x = \lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h}.$$

It does not give separate meanings to $dx$ and $dy$ , so $\der y x$ isn't a quotient. Nevertheless, people have tried to define $dy$ and $dx$ in sensible ways in order to make the quotient $\der y x$ equal the derivative.

Here is one way to do this. Regard $dx$ as an independent variable, and define $dy = f'(x)\,dx$ . Then formally have $\der y x = f'(x)$ . This has the following interpretation.

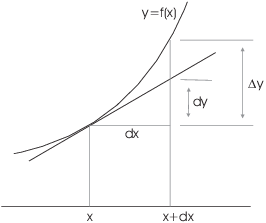
$$\hbox{\epsfysize=2in \epsffile{differentials-1.eps}}$$

The tangent line at a point on $y = f(x)$ has slope $f'(x)$ . If you move from x to $x + dx$ , the tangent line rises by $dy = f'(x)\,dx$ . On the other hand, the actual change in y is

$$\Delta y = f(x + dx) - f(x).$$

If $dx$ is small, $dy \approx \Delta y$ . Hence,

$$f'(x)\,dx \approx f(x + dx) - f(x), \quad\hbox{or}\quad f(x + dx) \approx f(x) + dx.$$

This formula can be used to approximate $f(x + dx)$ from $f(x)$ . I'll refer to this procedure as approximation by differentials, or the tangent line approximation.

Note that $\Delta f \approx df$ --- they're approximately equal. Somewhat confusingly, $\Delta x$ and $dx$ are often used interchangeably, so $\Delta x = dx$ . You might think of it this way: $\Delta x$ or $dx$ is the change in the input variable, which presumably you know exactly. But the change in f is given exactly by the corresponding change in the height of the graph of f, and given approximately by the corresponding change in the height of the tangent line to the graph of f.

Example. For $f(x) = x^3 + 2x - 4$ , find:

(a) The exact change in f if x goes from 1 to 1.01.

(b) The approximate change in f if x goes from 1 to 1.01.

(a) The exact change in f is $\Delta f = f(1.01) - f(1)$ .

$$f(1) = -1, \quad f(1.01) = -0.949699, \quad\hbox{so}\quad \Delta f = -0.949699 - (-1) = 0.050301.\quad\halmos$$

(b) The approximate change in f is $df = f'(x)\,dx$ . $f'(x) = 3x^2 + 2$ , so $f'(1) = 5$ . Since $dx = 1.01 - 1 = 0.01$ ,

$$df = 5\cdot 0.01 = 0.05.\quad\halmos$$

Notice that the approximate change differs from the exact change by only around 0.0003.

Example. Suppose $f(5) = 2.7$ and $f'(5) = -3$ . Find:

(a) The approximate change in f as x changes from 5 to 4.9.

(b) The approximate value of $f(4.9)$ .

(a) The approximate change in f is $df = \der f x\,dx$ . Now $dx = 4.9 - 5 = -0.1$ , while $f'(5) = -3$ . Thus,

$$df = (-3)(-0.1) = 0.3.\quad\halmos$$

(b) The approximate value of $f(4.9)$ is given by

$$f(4.9) \approx f(5) + df = 2.7 + 0.3 = 3.0.\quad\halmos$$

Example. A differentiable function $y = f(x)$ has derivative $f'(x) = \dfrac{x^2 + 5}{x^4 + 9}$ . Approximate the change in f that results when x changes from 1 to 1.02.

$$dx = 1.02 - 1 = 0.02 \quad\hbox{and}\quad f'(1) = \dfrac{1 + 5}{1 + 9} = \dfrac{6}{10} = 0.6.$$

Hence, the approximate change in f is

$$df = f'(1)\,dx = (0.6)(0.02) = 0.012.\quad\halmos$$

Example. A function is defined implicitly by the equation

$$x^2 y - 2 y^3 = 3 x^3 - 4.$$

Approximate the change in y at the point $(1,1)$ , as x changes from 1 to 1.01.

First, compute $y'$ by implicit differentiation:

$$x^2 y' + 2 x y - 6 y^2 y' = 9 x^2.$$

Set $x = 1$ , $y = 1$ :

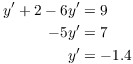
$$\eqalign{ y' + 2 - 6 y' & = 9 \cr -5 y' & = 7 \cr y' & = -1.4 \cr}$$

The change in x is $dx = 1.01 - 1 = 0.01$ . Therefore, the change in y is approximately

$$dy = y'(1)\,dx = (-1.4)(0.01) = -0.014.\quad\halmos$$

Example. Use differentials to approximate $\sqrt{1.01}$ .

Since I'm trying to approximate $\sqrt{1.01}$ , I'll let $f(x) = \sqrt{x}$ .

I know that $f(1) = \sqrt{1} = 1$ ; I'll use differentials to approximate the change in going from 1 to 1.01. First,

$$f'(x) = \dfrac{1}{2 \sqrt{x}}, \quad\hbox{so}\quad f'(1) = \dfrac{1}{2}.$$

The change in x is

$$dx = (\hbox{ugly point}) - (\hbox{nice point}) = 1.01 - 1 = 0.01.$$

Then

$$df = f'(1)\,dx = \dfrac{1}{2} \cdot 0.01 = 0.005.$$

Hence,

$$\sqrt{1.01} = f(1.01) \approx f(1) + df = 1 + 0.005 = 1.005.$$

The actual value is 1.004988.

In some applications, you can interpret $\Delta w$ as the error in w. In this case, $dw$ is the approximate error in w.

In some cases, you need to know how large the error is relative to the thing you're measuring. For instance, an error of 1 cm in measuring something of length 10 cm is fairly large: It is an error of $\dfrac{1}{10} = 10%$ . But an error of 1 cm in measuring something of length 100 cm is an error of $\dfrac{1}{100} = 1%$ .

The relative error in w is $\dfrac{\Delta w}{w}$ , and the approximate relative error is $\dfrac{dw}{w}$ . A relative error is often expressed as a percentage.

Example. The side of a square is measured to be 10 light-years, with an error of 0.2 light-years.

(a) Use differentials to approximate the error in the area.

(b) Approximate the relative error and the relative percentage error.

(a) If s is the length of the side, the area is $A = s^2$ . Then $A' = 2 s$ , so $A'(10) = 20$ . The error $\Delta A$ is approximated by

$$dA = A'(10)\,ds = 20 \cdot 0.2 = 4 \quad\hbox{light-years}^2.\quad\halmos$$

(b) For $s = 10$ , the area is $A = 10^2 = 100$ . The approximate relative error is $\dfrac{4}{100} = 4%$ .

[1] Carl B. Boyer, The History of the Calculus and Its Conceptual Development. New York: Dover Publications, 1949. [ISBN 0-486-60509-4]

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga