While it's possible to compute derivatives using the definition of the derivative as a limit, it is too much work if you're differentiating anything complicated. It's more efficient to develop a set of differentiation rules to use as shortcuts.
Before we start, here are several comments. First, it is silly to memorize the rules. You should learn them by doing examples.
Second, computing derivatives is a skill --- it is something you learn by practicing. You can't learn to differentiate by watching the instructor do examples. Since you will need to compute derivatives in virtually all the calculus courses you take, it is worth learning to do well now to avoid grief in the future.
On the other hand, you should keep things in perspective. Calculus is not just a matter of computing derivatives and integrals. The computations acquire their meaning when they are used to do things: Compute rates of change, find maxima and minima, determine areas or volumes, and so on.
The fact that calculators and computers can do arithmetic does not mean that people don't need to learn arithmetic. A certain amount of computation is necessary in order to develop an intuition for numbers.
In the same way, the fact that computer programs can compute derivatives and integrals does not mean that people don't need to learn to differentiate or integrate. I don't think you can have a complete understanding of what a derivative is if you've never computed a few derivatives. However, at some point you may want to use a computer to do the ugly computations, in the same way that you use a calculator to do arithmetic.
I'll illustrate the differentiation rules with some examples. In
these examples, I'll write "![]() " for the derivative of
" for the derivative of ![]() with respect to x.
with respect to x.
1. ( Derivative of a Constant) The derivative of a constant is 0.
This makes sense, because a constant doesn't change, and the derivative gives the rate of change.
Thus,
![]()
![]()
![]()
Proofs of the derivative rules depend on the properties we proved for limits. I'll give proofs of some of the rules by way of example.
Proof. (The Derivative of a Constant) In this
case, ![]() , where c is a constant. This means that
the output of f is c, no matter what the input is. Hence,
, where c is a constant. This means that
the output of f is c, no matter what the input is. Hence,
![]() as well. Then
as well. Then
![]()
2. ( The Power Rule) ![]() , if n is a nonzero
integer.
, if n is a nonzero
integer.
This rule is called the Power Rule, because it tells you how to differentiate a power of the variable. In words, you "bring the power down" and decrease the power by 1.
Example.
![]()
![]()
![]()
Notice that n can be any nonzero real number:
![]()
Proof. (Power Rule) I'll just consider the
case where n is a positive integer. the proof will use the Binomial Formula, which I'll give below. Let ![]() . Then
. Then
![]()
If ![]() , this comes out to
, this comes out to
![]()
This is the same as ![]() , so the
formula works. So assume that
, so the
formula works. So assume that ![]() .
.
Recall that ![]() ( n
factorial) is the product of the integers from 1 to n:
( n
factorial) is the product of the integers from 1 to n:
![]()
The binomial formula says
![]()
Therefore,
![]()
Next, divide by h:
![]()
As ![]() , all the terms but the first go to 0,
because they contain positive powers of h. Therefore,
, all the terms but the first go to 0,
because they contain positive powers of h. Therefore,
![]()
I simplified the fraction by writing
![]()
If n is a negative integer, you can use the result for positive
powers together with the Quotient Rule. For
more general powers, the easiest way to prove the Power rule is to
express ![]() as
as ![]() . This
requires knowing the differentiation rules for
. This
requires knowing the differentiation rules for ![]() and
and ![]() , as well as the Chain
Rule.
, as well as the Chain
Rule.![]()
3. ( Multiplication by Constants) ![]() .
.
This rule says that constants may be "pulled out" when you differentiate. Another way to think of this is that the constant just "sits there", while the thing it multiplies gets differentiated.
Don't confuse this rule with the first rule --- the derivative of a constant is 0. In that situation, the constant was "by itself". In this situation, the constant multiplies something.
Example. Compute ![]() .
.
By the Power Rule and the Multiplication by Constants rule,
![]()
With some experience, most people will just multiply the 8 and the 10
in their heads and write "80" in one step.![]()
Example. I'll discuss trig functions later on, and I'll show that
![]()
Compute ![]() .
.
![]()
The second derivative of f is the derivative
of ![]() with respect to x. It's denoted
with respect to x. It's denoted ![]() . Thus,
. Thus,
![]()
Likewise, the third derivative is the derivative of the second derivative, and so on:
![]()
Example. Compute the first, second, and third
derivatives of ![]() .
.
![]()
Definition. A function ![]() has a vertical tangent at a if
f is continuous at a and
has a vertical tangent at a if
f is continuous at a and
![]()
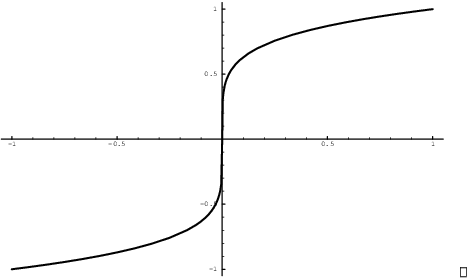
Example. Show that ![]() has a vertical tangent at
has a vertical tangent at ![]() .
.
I have ![]() , so
, so
![]()
Thus, the graph has a vertical tangent at ![]() . Picture:
. Picture:
Definition. A function ![]() has a cusp at a if f is
continuous at a and:
has a cusp at a if f is
continuous at a and:
(a) ![]() approaches
approaches ![]() from one side of a.
from one side of a.
(b) ![]() approaches
approaches ![]() from the other side of a.
from the other side of a.
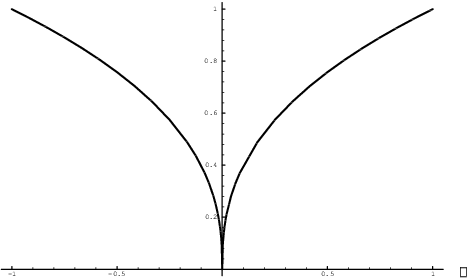
Example. Show that ![]() has a cusp at
has a cusp at ![]() .
.
I have ![]() , so
, so
![]()
Thus, ![]() has a cusp at
has a cusp at ![]() . Here's the graph:
. Here's the graph:
4. ( Sums) The derivative of a sum is the sum of the derivatives:
![]()
Example. Compute ![]() .
.
It's a good idea to write ![]() as
as ![]() (and in general, to write
(and in general, to write ![]() as
as ![]() ). That way, you
can see the number power to apply the Power Rule.
). That way, you
can see the number power to apply the Power Rule.
![]()
5. ( The Product Rule)
![]()
The formula above is the traditional way this rule is stated. However, if you are trying to remember this rule, it's useful to remember it in a way that makes it easy to recite, and so that the statement tells you what to do. Here's what I'd suggest.
I'll write "D" to mean "the derivative of". Then the rule is
![]()
This makes it easy to recite, and it comes out like: "The first times the derivative of the second plus the second times the derivative of the first." --- or maybe: "first-D-second-plus-second-D-first" for short.
The point is that by using "first" and "second" instead of random symbols like "u" and "v" (a popular choice), the statement of the rule tells you what to do.
Example. Compute ![]() .
.
Note: In problems like this, you don't need to multiply answers out unless you're asked to.
![]()
The following picture shows why the Product Rule works.
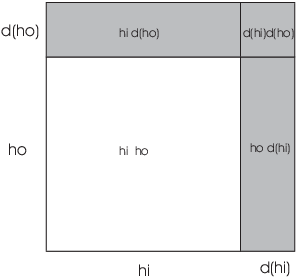
If I change ![]() by a small amount
by a small amount ![]() and
and ![]() by a small
amount
by a small
amount ![]() the change in the product
the change in the product ![]() is
is
![]()
However, the last term is a product of two small numbers, which is very small compared to the other two terms. I may neglect it, and I obtain
![]()
Now divide by ![]() to pass to rates of change. Here's
the formal proof using limits.
to pass to rates of change. Here's
the formal proof using limits.
Proof. (Product Rule)
![]()
![]()
![]()
![]()
![]()
I'll give the next rule in a form that makes it easy to recite, as I did with the Product Rule.
6. ( The Quotient Rule)
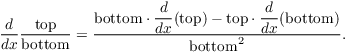
Some people prefer "hi" and "lo", Take your pick.
Example. (a) Compute ![]() .
.
(b) Compute ![]() .
.
(a)
![]()
(b) If either the top or the bottom is just a number, it is better not to use the Quotient Rule. If the number is on the bottom, you can divide:
![]()
I'll note now that if the number is on the top, you can use
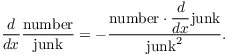
You shouldn't memorize this formula; it's a special case of the Chain Rule, which I'll talk about later. But in case you want to try it, here's an example:
![]()
Sometimes it's useful to express the differentiation rules using the "prime" notation. Here are the rules for sums, products, and quotients:
(a) (Sums) ![]() .
.
(b) (Products) ![]()
(c) (Quotients) ![]() .
.
Example. Suppose f and g are differentiable functions satisfying
![]()
(a) Find ![]() .
.
(b) Find ![]() .
.
(a)
![]()
(b)
![]()
I obtained the derivative by trying to find the slope of the tangent line to a curve. Here are some examples which apply the differentiation rules to problems on tangent lines.
Example. Find the equation of the tangent
lines to ![]() which pass through the point
which pass through the point ![]() .
.
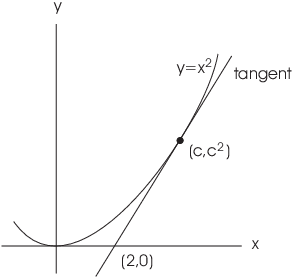
The x-axis is clearly one such tangent line. Its equation is ![]() .
.
To find the other tangent, let ![]() be the point of tangency. The slope of the tangent
line is
be the point of tangency. The slope of the tangent
line is ![]() ; when
; when ![]() ,
, ![]() .
.
On the other hand, the line passes through ![]() and
and ![]() , so its slope is
, so its slope is
![]() . equate the two expressions
for the slope and solve for c:
. equate the two expressions
for the slope and solve for c:
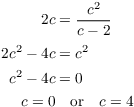
![]() gives the x-axis, which I know about
already.
gives the x-axis, which I know about
already. ![]() gives
gives ![]() ; since the line passes through
; since the line passes through ![]() , its equation is
, its equation is
![]()
Example. At what point(s) does the graph of
![]() have a horizontal tangent?
have a horizontal tangent?
A horizontal line has slope 0. Since the derivative gives the slope of the tangent, I'll find the derivative and set it equal to 0:
![]()
Clearly, ![]() when
when ![]() .
. ![]() , so there is a
horizontal tangent at the point
, so there is a
horizontal tangent at the point ![]() .
.![]()
Example. Find the equation of the line which
is perpendicular to the graph of ![]() at the point
at the point ![]() .
.
To be perpendicular to the graph is the same as being perpendicular
to the tangent line. The slope of the tangent is given by the
derivative, which is ![]() . Hence, at
. Hence, at ![]() , the tangent has slope
, the tangent has slope ![]() .
.
Perpendicular line have slopes which are negative reciprocals of each
other. Therefore, the slope of the perpendicular line is ![]() . Since the line passes through the point
. Since the line passes through the point
![]() , its equation is
, its equation is
![]()
Copyright 2018 by Bruce Ikenaga