Graphing

Calculus provides information which is useful in graphing curves.

(i) The first derivative $y'$ tells where a curve is increasing and where a curve is decreasing.

(ii) The second derivative $y''$ tells where a curve is concave up and where a curve is concave down.

I'll put this information together with some other techniques into a step-by-step graphing procedure. Here it is:

1. Find the domain of the function.

2. Find the x-intercepts (by setting $y = 0$ and solving for x) and the y-intercept (by setting $x = 0$ and solving for y).

Note: There may not be any intercepts of a given kind. If it's too difficult to solve for exact x-intercepts, you may want to use a calculating device to approximate them.

3. Find the derivatives $y'$ and $y''$ .

4. Use a sign chart for $y'$ to find where the graph increases and where it decreases.

5. Use the $y'$ -sign chart to locate any local maxima or minima.

6. Use a sign chart for $y''$ to find where the graph is concave up and where it is concave down.

7. Use the $y''$ -sign chart to locate any inflection points.

8. By computing the appropriate limits, determine whether the graph has any vertical or horizontal asymptotes.

Check for horizontal asymptotes by computing

$$\lim_{x \to +\infty} f(x) \quad\hbox{and}\quad \lim_{x \to -\infty} f(x).$$

To locate any vertical asymptotes, look for isolated points or endpoints which are not in the domain. If $x = c$ is such a point, compute

$$\lim_{x \to c^+} f(x) \quad\hbox{and}\quad \lim_{x \to c^-} f(x).$$

9. Use the information you've obtained to sketch the graph.

You might wonder why it's necessary to go through all this trouble when graphing calculators and computers can draw graphs of functions. A calculator or a computer can't tell what features of a graph are interesting to people. You can't tell a computer to focus on an interesting feature unless you know --- by methods like those above --- that the interesting feature is there to begin with!

In one of the examples, I'll use the graphing procedure on $y = \dfrac{x + 1}{6(x + 3)^3}$ . At the end of the example is a picture of the graph drawn by a computer. Look at the picture now. Can you tell from the picture that there's a local max at $x = 0$ ? I know there is, because calculus says so!

Example. Graph $y = \dfrac{3}{x} - \dfrac{2}{x^3} = \dfrac{3 x^2 - 2}{x^3}$ .

The domain is $x \ne 0$ .

The x-intercepts are $x = \pm \sqrt{\dfrac{2}{3}} \approx \pm 0.81650$ .

There is no y-intercepts.

The derivatives are:

$$y' = \dfrac{-3(x^2 - 2)}{x^4} \quad\hbox{and}\quad y'' = \dfrac{6(x^2 - 4)}{x^5}.$$

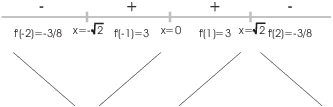
$$\hbox{\epsfxsize=3in \epsffile{graphing-1i.eps}}$$

The function increases for $-\sqrt{2} \le x < 0$ and for $0 < x \le \sqrt{2}$ . The function decreases for $x \le -\sqrt{2}$ and for $x \ge \sqrt{2}$ .

The is a local max at $x = \sqrt{2}$ and a local min at $x = -\sqrt{2}$ .

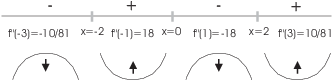
$$\hbox{\epsfxsize=3in \epsffile{graphing-1c.eps}}$$

The function is concave up for $-2 < x < 0$ and for $x > 2$ . The function is concave down for $x < -2$ and for $0 < x < 2$ .

There are inflection points at $x = -2$ and at $x = 2$ .

The graph is asymptotic to $y = 0$ as $x \to +\infty$ and as $x \to -\infty$ .

There is a vertical asymptote at $x = 0$ :

$$\lim_{x \to 0^+} \dfrac{3 x^2 - 2}{x^3} = -\infty, \quad \lim_{x \to 0^-} \dfrac{3 x^2 - 2}{x^3} = +\infty.$$

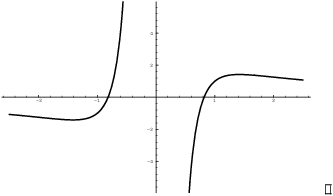
$$\hbox{\epsfysize=1.75in \epsffile{graphing-1g.eps}}\quad\halmos$$

Example. Graph $y = x + \dfrac{1}{x - 2}$ .

The domain is $x \ne 2$ .

The x-intercept is $x = 1$ .

The y-intercepts is $y = -\dfrac{1}{2}$ .

The derivatives are

$$y' = 1 - \dfrac{1}{(x - 2)^2} = \dfrac{(x - 1)(x - 3)}{(x - 2)^2} \quad\hbox{and}\quad y'' = \dfrac{2}{(x - 2)^3}.$$

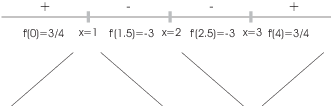
$$\hbox{\epsfxsize=3in \epsffile{graphing-2i.eps}}$$

The function increases for $x \le 1$ and for $x \ge 3$ . The function decreases for $1 \le x < 2$ and for $2 < x \le 3$ .

There is a local max at $x = 1$ and a local min at $x = 3$ .

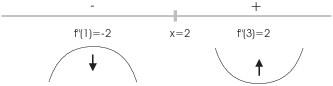
$$\hbox{\epsfxsize=3in \epsffile{graphing-2c.eps}}$$

The function is concave up for $x > 2$ and concave down for $x < 2$ .

There is an inflection point at $x = 2$ .

There are no horizontal asymptotes.

There is a vertical asymptote at $x = 2$ :

$$\lim_{x \to 2^+} \left(x + \dfrac{1}{x - 2}\right) = +\infty, \quad \lim_{x \to 2^-} \left(x + \dfrac{1}{x - 2}\right) = -\infty.$$

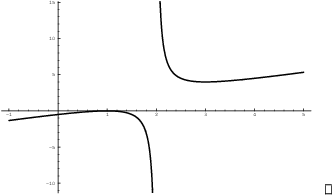
$$\hbox{\epsfysize=1.75in \epsffile{graphing-2g.eps}}\quad\halmos$$

Example. Graph $y = \dfrac{x + 1}{6(x + 3)^3}$ .

The domain is $x \ne -3$ .

The x-intercept is $x = -1$ .

The y-intercept is $y = \dfrac{1}{162}$ .

The computations of $y'$ and $y''$ are a bit messy, so you may want to skip to the final results and go on to the increasing-decreasing section.

To compute $y'$ , I'll use the Quotient Rule. First, write the function this way:

$$y = \dfrac{1}{6} \dfrac{x + 1}{(x + 3)^3}.$$

Differentiate:

$$y' = \dfrac{1}{6} \dfrac{(x + 3)^3 (1) - (x + 1) (3) (x + 3)^2}{(x + 3)^6} = \dfrac{1}{6} \dfrac{(x + 3) - (x + 1)(3)}{(x + 3)^4} = \dfrac{1}{6} \dfrac{(x + 3) - (3 x + 3)}{(x + 3)^4} =$$

$$\dfrac{1}{6} \dfrac{-2 x}{(x + 3)^4} = -\dfrac{1}{3} \dfrac{x}{(x + 3)^4}.$$

I could compute $y''$ using the Quotient Rule, but for variety I'll use an algebra trick that is sometimes useful. Before differentiating, I'll rewrite $y'$ this way:

$$y' = -\dfrac{1}{3} \dfrac{x}{(x + 3)^4} = -\dfrac{1}{3} \dfrac{(x + 3) - 3}{(x + 3)^4} = -\dfrac{1}{3} \left(\dfrac{x + 3}{(x + 3)^4} - \dfrac{3}{(x + 3)^4}\right) = -\dfrac{1}{3} \left(\dfrac{1}{(x + 3)^3} - \dfrac{3}{(x + 3)^4}\right) =$$

$$-\dfrac{1}{3} \left((x + 3)^{-3} - 3 (x + 3)^{-4}\right).$$

Now differentiate:

$$y'' = -\dfrac{1}{3} \left(-3 (x + 3)^{-4} + 12 (x + 3)^{-5}\right) = -\dfrac{1}{3} \left(\dfrac{-3}{(x + 3)^4} + \dfrac{12}{(x + 3)^5}\right) =$$

$$-\dfrac{1}{3} \left(\dfrac{-3}{(x + 3)^4} \cdot \dfrac{x + 3}{x + 3} + \dfrac{12}{(x + 3)^5}\right) = -\dfrac{1}{3} \left(\dfrac{-3 (x + 3) + 12}{(x + 3)^5}\right) = -\dfrac{1}{3} \left(\dfrac{-3 x - 9 + 12}{(x + 3)^5}\right) =$$

$$-\dfrac{1}{3} \left(\dfrac{-3 x + 3}{(x + 3)^5}\right) = \dfrac{x + 1}{(x + 3)^5}.$$

$y' = 0$ for $x = 0$ and $y'$ is undefined for $x = -3$ . Since the function is undefined at $x = -3$ , this point can't be a max or a min.

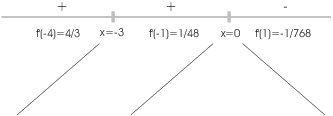
$$\hbox{\epsfxsize=3in \epsffile{graphing-3i.eps}}$$

The function increases for $x < -3$ and for $-3 < x \le 0$ . The function decreases for $x \ge 0$ .

There is a local max at $x = 0$ .

$y'' = 0$ for $x = -1$ and $y''$ is undefined for $x = -3$ . Since the function is undefined at $x = -3$ , this point can't be an inflection point.

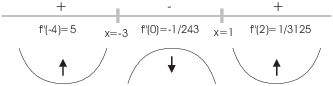
$$\hbox{\epsfxsize=3in \epsffile{graphing-3c.eps}}$$

The function is concave up for $x < -3$ and for $x > 1$ . The function is concave down for $-3 < x < 1$ .

There is an inflection point at $x = 1$ .

The graph is asymptotic to $y = 0$ as $x \to +\infty$ and as $x \to -\infty$ .

There is a vertical asymptotes at $x = -3$ :

$$\lim_{x \to -3^+} \dfrac{x + 1}{(6 (x + 3)^3} = -\infty, \quad \lim_{x \to -3^-} \dfrac{x + 1}{(6 (x + 3)^3} = +\infty.$$

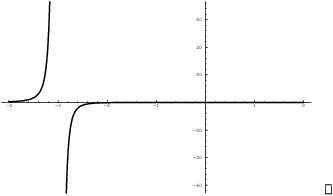
$$\hbox{\epsfysize=1.75in \epsffile{graphing-3g.eps}}\quad\halmos$$

Example. Graph $y = \dfrac{9}{88} x^{11/3} - \dfrac{18}{5} x^{5/3}$ .

The domain consists of all real numbers.

The x-intercepts are $x \approx \pm 5.93296$ .

The y-intercept is $y = 0$ .

Here's the computation of $y'$ :

$$y' = \dfrac{3}{8} x^{8/3} - 6 x^{2/3} = \dfrac{3}{8} (x^{8/3} - 16 x^{2/3}) = \dfrac{3}{8} x^{2/3} (x^2 - 16) = \dfrac{3}{8} x^{2/3} (x - 4)(x + 4).$$

To compute $y''$ , I differentiate $y' = \dfrac{3}{8} x^{8/3} - 6 x^{2/3}$ :

$$y'' = x^{2/3} - 4 x^{-1/3} = x^{2/3} - \dfrac{4}{x^{1/3}} = x^{2/3} \cdot \dfrac{x^{1/3}}{x^{1/3}} - \dfrac{4}{x^{1/3}} = \dfrac{x^2 - 4}{x^{1/3}} = \dfrac{(x - 2)(x + 2)}{x^{1/3}}.$$

$y' = 0$ for $x = 0$ , $x = 4$ , and $x = -4$ , and $y'$ is defined for all x.

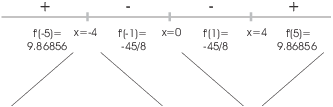
$$\hbox{\epsfxsize=3in \epsffile{graphing-4i.eps}}$$

The function increases for $x \le -4$ and for $x \ge 4$ . It decreases for $-4 \le x \le 4$ .

There is a local max at $x = -4$ and a local min at $x = 4$ . $x = 0$ is neither a max nor a min.

$y'' = 0$ for $x = 2$ and $x = -2$ , and $y''$ is undefined at $x = 0$ . Since the function is defined at $x = 0$ , there could be an inflection point there.

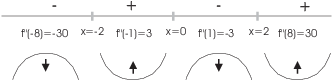
$$\hbox{\epsfxsize=3in \epsffile{graphing-4c.eps}}$$

The function is concave up for $-2 < x < 0$ and for $x > 2$ . It is concave down for $x < -2$ and for $0 < x < 2$ . There are inflection points at $x = -2$ , $x = 0$ , and $x = 2$ .

There are no vertical or horizontal asymptotes.

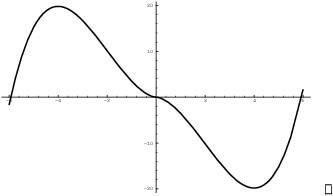
$$\hbox{\epsfysize=1.75 in \epsffile{graphing-4g.eps}}\quad\halmos$$

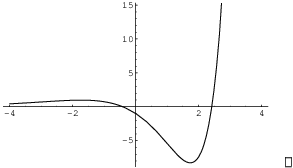
Example. Graph $y = (x^2 - 2 x - 1) e^x$ .

The domain is all real numbers.

The x-intercepts are

$$x = \dfrac{2 \pm \sqrt{4 + 4}}{2} = 1 \pm \sqrt{2}.$$

The y-intercept is $y = -1$ .

The derivatives are

$$y' = (x^2 - 2 x - 1)e^x + (2 x - 2)e^x = (x^2 - 3)e^x = (x - \sqrt{3})(x + \sqrt{3})e^x,$$

$$y'' = (x^2 - 3)e^x + 2 x e^x = (x^2 + 2 x - 3)e^x = (x + 3)(x - 1)e^x.$$

$y'$ is defined for all x. $y' = 0$ for $x = \pm \sqrt{3}$ .

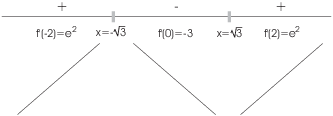
$$\hbox{\epsfxsize=3in \epsffile{graphing-5i.eps}}$$

The function increases for $x \le -\sqrt{3}$ and for $x \ge \sqrt{3}$ ; it decreases for $-\sqrt{3} \le x \le \sqrt{3}$ .

There is a local max at $x = -\sqrt{3}$ and a local min at $x = \sqrt{3}$ .

$y''$ is defined for all x. $y'' = 0$ for $x = -3$ and for $x = 1$ .

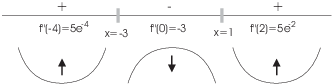
$$\hbox{\epsfxsize=3in \epsffile{graphing-5c.eps}}$$

The function is concave up for $x < -3$ and for $x > 1$ ; it is concave down for $-3 < x < 1$ .

$x = -3$ and $x = 1$ are inflection points.

There are no vertical asymptotes.

$$\lim_{x \to +\infty} \left((x^2 - 2 x - 1)e^x\right) = +\infty \quad\hbox{and}\quad \lim_{x \to -\infty} \left((x^2 - 2 x - 1)e^x\right) = 0.$$

$y = 0$ is a horizontal asymptote at $-\infty$ .

$$\hbox{\epsfysize=1.5in \epsffile{graphing-5g.eps}}\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga