Growth and Decay Models

In certain situations, the rate at which a thing grows or decreases is proportional to the amount present.

When a substance undergoes radioactive decay, the release of decay particles precipitates additional decay as the particles collide with the atoms of the substance. The larger the mass, the larger the number of collisions per unit time.

Consider a collection of organisms growing without environmental constraints. The larger the population, the larger the number of individuals involved in reproduction --- and hence, the higher the reproductive rate.

Let P be the amount of whatever is being measured --- the mass of the radioactive substance or the number of organisms, for example. Let t be the time elapsed since the measurements were started. Then

$$\der P t = k P.$$

If $k > 0$ , then P increases with time ( exponential growth); if $k < 0$ , then P decreases with time ( exponential decay). k is called the growth constant (or decay constant).

I'll solve for P in terms of t using separation of variables. First, formally move the P's to one side and the t's to the other:

$$\dfrac{dP}{P} = k\,dt.$$

Integrate both sides and solve for P:

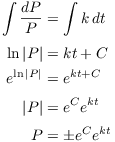
$$\eqalign{ \int \dfrac{dP}{P} & = \int k\,dt \cr \noalign{\vskip2pt} \ln |P| & = k t + C \cr e^{\ln |P|} & = e^{k t + C} \cr \noalign{\vskip2pt} |P| & = e^C e^{k t} \cr \noalign{\vskip2pt} P & = \pm e^C e^{k t} \cr}$$

Let $P_0 = \pm e^C$ . This gives

$$P = P_0 e^{k t}.$$

Note that $P_0$ is the initial amount: Setting $t = 0$ , $P(0) = P_0 e^0 = P_0$ .

Example. A population of roaches grows exponentially under Calvin's couch. There are 20 initially and 140 after 2 days. How many are there after 14 days?

If P is the number of roaches after t days, then

$$P = 20 e^{k t}.$$

When $t = 2$ , $P = 140$ :

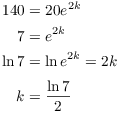
$$\eqalign{ 140 & = 20 e^{2 k} \cr 7 & = e^{2 k} \cr \ln 7 & = \ln e^{2 k} = 2 k \cr \noalign{\vskip2pt} k & = \dfrac{\ln 7}{2} \cr}$$

Hence,

$$P = 20 e^{(t \ln 7)/2}.$$

When $t = 14$ ,

$$P = 20 e^{(14 \ln 7)/2} \approx 16470860\ \hbox{roaches}.\quad\halmos$$

Remark. We'll often have expressions of the form "$e^{(\hbox{stuff})}$ ", and this can be inconvenient to write if "stuff" is complicated. You can use the exponential function notation to avoid this problem:

$$\exp (\hbox{stuff}) = e^{(\hbox{stuff})}.$$

For instance, in the last example,

$$\exp \left(\dfrac{\ln 7}{2} t\right) = e^{(t \ln 7)/2}.$$

Example. A population of MU flu virus grows in such a way that it triples every 5 hours. If there were 100 initially, when will there be 1000000?

Let N be the number of the little rascals at time t. Then

$$N = 100 e^{k t}.$$

Since the amount triples in 5 hours, when $t = 5$ , $N = 300$ :

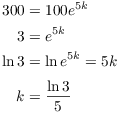
$$\eqalign{ 300 & = 100 e^{5 k} \cr 3 & = e^{5 k} \cr \ln 3 & = \ln e^{5 k} = 5 k \cr \noalign{\vskip2pt} k & = \dfrac{\ln 3}{5} \cr}$$

Hence,

$$N = 100 e^{(t \ln 3)/5}.$$

Set $N = 1000000$ :

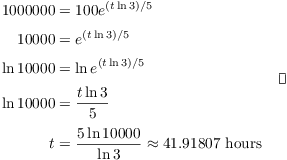
$$\eqalign{ 1000000 & = 100 e^{(t \ln 3)/5} \cr \noalign{\vskip2pt} 10000 & = e^{(t \ln 3)/5} \cr \noalign{\vskip2pt} \ln 10000 & = \ln e^{(t \ln 3)/5} \cr \noalign{\vskip2pt} \ln 10000 & = \dfrac{t \ln 3}{5} \cr \noalign{\vskip2pt} t & = \dfrac{5 \ln 10000}{\ln 3} \approx 41.91807\ \hbox{hours} \cr}\quad\halmos$$

The half-life of a radioactive substance is the amount of time it takes for a given mass M to decay to $\dfrac{M}{2}$ . Note that in radioactive decay, this time is independent of the amount M. That is, it takes the same amount of time for 100 grams to decay to 50 grams as it takes for 1000000 grams to decay to 500000 grams.

Example. The half-life of radium is 1620 years. How long will it take 100 grams of radium to decay to 1 gram?

Let M be the amount of radium left after t years. Then

$$M = 100 e^{k t}.$$

When $t = 1620$ , $M = 50$ :

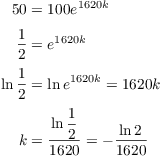
$$\eqalign{ 50 & = 100 e^{1620 k} \cr \noalign{\vskip2pt} \dfrac{1}{2} & = e^{1620 k} \cr \noalign{\vskip2pt} \ln \dfrac{1}{2} & = \ln e^{1620 k} = 1620 k \cr \noalign{\vskip2pt} k & = \dfrac{\ln \dfrac{1}{2}}{1620} = -\dfrac{\ln 2}{1620} \cr}$$

Hence,

$$M = 100 e^{-(t \ln 2)/1620}.$$

Set $M = 1$ :

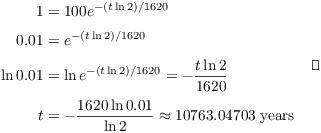
$$\eqalign{ 1 & = 100 e^{-(t \ln 2)/1620} \cr \noalign{\vskip2pt} 0.01 & = e^{-(t \ln 2)/1620} \cr \noalign{\vskip2pt} \ln 0.01 & = \ln e^{-(t \ln 2)/1620} = -\dfrac{t \ln 2}{1620} \cr \noalign{\vskip2pt} t & = -\dfrac{1620 \ln 0.01}{\ln 2} \approx 10763.04703\ \hbox{years} \cr}\quad\halmos$$

Example. A population of bacteria grows exponentially in such a way that there are 100 after 2 hours and 750 after 4 hours. How many were there initially?

Let P be the number of bacteria at time t. Then

$$P = P_0 e^{k t}.$$

There are 100 after 2 hours:

$$100 = P_0 e^{2 k}.$$

There are 750 after 4 hours:

$$750 = P_0 e^{4 k}.$$

I'll solve for k first. Divide the second equation by the first:

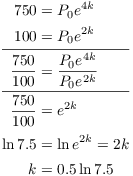
$$\eqalign{ 750 & = P_0 e^{4 k} \cr 100 & = P_0 e^{2 k} \cr \noalign{\vskip2pt \hrule \vskip2pt} \dfrac{750}{100} & = \dfrac{P_0 e^{4 k}}{P_0 e^{2 k}} \cr \noalign{\vskip2pt \hrule \vskip2pt} \dfrac{750}{100} & = e^{2 k} \cr \noalign{\vskip2pt} \ln 7.5 & = \ln e^{2 k} = 2 k \cr \noalign{\vskip2pt} k & = 0.5 \ln 7.5 \cr}$$

Plug this into the first equation:

$$100 = P_0 e^{2\cdot 0.5 \ln 7.5} = P_0 e^{\ln 7.5} = 7.5 P_0, \quad P_0 = \dfrac{100}{7.5} \approx 13.33333.$$

There were 13 bacteria initially (if I round to the nearest bacterium).

Newton's Law of Cooling.

According to Newton's law of cooling, the rate at which a body heats up or cools down is proportional to the difference between its temperature and the temperature of its environment.

If T is the temperature of the object and $T_e$ is the temperature of the environment, then

$$\der T t = k(T - T_e).$$

If $k > 0$ , the object heats up (an oven). If $k < 0$ , the object cools down (a refrigerator).

I'll solve the equation using separation of variables. Formally move the T's to one side and the t's to the other, then integrate:

$$\dfrac{dT}{T - T_e} = k\,dt, \quad \int \dfrac{dT}{T - T_e} = \int k\,dt, \quad \ln |T - T_e| = k t + C, \quad e^{\ln |T - T_e|} = e^{k t+C},$$

$$|T - T_e| = e^Ce^{k t}, \quad T - T_e = \pm e^C e^{k t}.$$

Let $C_0 = \pm e^C$ :

$$T - T_e = C_0 e^{k t}, \quad T = T_e + C_0 e^{k t}.$$

Let $T_0$ be the initial temperature --- that is, the temperature when $t = 0$ . Then

$$T_0 = T_e + C_0 e^0 = T_e + C_0, \quad C_0 = T_0 - T_e.$$

Thus,

$$T = T_e + (T_0 - T_e) e^{k t}.$$

Example. A $120^\circ$ bagel is placed in a $70^\circ$ room to cool. After 10 minutes, the bagel's temperature is $90^\circ$ . When will its temperature be $80^\circ$ ?

In this case, $T_e = 70$ and $T_0 = 120$ , so

$$T = 70 + 50 e^{k t}.$$

When $t = 10$ , $T = 90$ :

$$90 = 70 + 50 e^{10 k}, \quad 0.4 = e^{10 k}, \quad \ln 0.4 = \ln e^{10 k} = 10 k, \quad k = \dfrac{\ln 0.4}{10}.$$

Hence,

$$T = 70 + 50 e^{(t \ln 0.4)/10}.$$

Set $T = 80$ :

$$80 = 70 + 50 e^{(t \ln 0.4)/10}, \quad 0.2 = e^{(t \ln 0.4)/10}, \quad \ln 0.2 = \ln e^{(t \ln 0.4)/10} = \dfrac{t \ln 0.4}{10},$$

$$t = \dfrac{10 \ln 0.2}{\ln 0.4} \approx 17.56471\ \hbox{min}.\quad\halmos$$

Example. A pair of shoes is placed in a $300^\circ$ oven to bake. The temperature is $120^\circ$ after 10 minutes and $152.7^\circ$ after 20 minutes. What was the initial temperature of the shoes?

I set $T_e = 300$ in $T = T_e + (T_0 - T_e) e^{k t}$ to obtain

$$T = 300 + (T_0 - 300) e^{k t}.$$

When $t = 10$ , $T = 120$ :

$$120 = 300 + (T_0 - 300) e^{10 k}, \quad -180 = (T_0 - 300) e^{10 k}.$$

When $t = 20$ , $T = 152.7$ :

$$152.7 = 300 + (T_0 - 300) e^{20 k}, \quad -147.3 = (T_0 - 300) e^{20 k}.$$

Divide $-180 = (T_0 - 300) e^{10 k}$ by $-147.3 = (T_0 - 300) e^{20 k}$ and solve for k:

$$\dfrac{180}{147.3} = e^{-10 k}, \quad \ln \dfrac{180}{147.3} = \ln e^{-10 k} = -10 k, \quad k = -\dfrac{1}{10} \ln \dfrac{180}{147.3}.$$

Plug this back into $-180 = (T_0 - 300) e^{10 k}$ and solve for $T_0$ :

$$-180 = (T_0 - 300) e^{[10\cdot (-1/10) \ln (180/147.3)]}, \quad -180 = (T_0 - 300) e^{-\ln (180/147.3)},$$

$$-180 = (T_0 - 300) e^{\ln (147.3/180)}, \quad -180 = (T_0 - 300)\cdot \dfrac{147.3}{180},$$

$$-\dfrac{32400}{147.3} = T_0 - 300, \quad T_0 = 300 - \dfrac{32400}{147.3} \approx 80.04073^\circ.\quad\halmos$$

In the real world, things do not grow exponentially without limit. It's natural to try to find models which are more realistic.

Logistic Growth.

The logistic growth model is described by the differential equation

$$\der P t = k P (b - P).$$

P is the quantity undergoing growth --- for example, an animal population --- and t is time. k is the growth constant, and the constant b is called the carrying capacity; the reason for the name will become evident shortly.

Notice that if P is less than b and is small compared to b, then $b - P \approx b$ . The equation becomes $\der P t \approx kbP$ , which is exponential growth. Notice that the derivative $\der P t$ is positive, so P increases with time.

If P is greater than b, then $b - P$ is negative, so the derivative $\der P t$ is negative. This means that P decreases with time.

It's possible to solve the logistic equation using separation of variables, though it will require a little trick (called a partial fraction expansion).

Separate the variables:

$$\int \dfrac{dP}{P(b - P)} = \int k\,dt.$$

Now

$$\dfrac{1}{P(b - P)} = \dfrac{1}{b}\left(\dfrac{1}{b - P} + \dfrac{1}{P}\right).$$

(You can verify that this is correct by adding the fractions on the right over a common denominator.) Therefore, I have

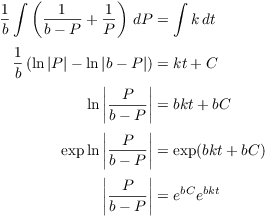
$$\eqalign{ \dfrac{1}{b}\int \left(\dfrac{1}{b - P} + \dfrac{1}{P}\right)\,dP & = \int k\,dt \cr \noalign{\vskip2 pt} \dfrac{1}{b}\left(\ln |P| - \ln |b - P|\right) & = k t + C \cr \noalign{\vskip2 pt} \ln \left|\dfrac{P}{b - P}\right| & = b k t + b C \cr \noalign{\vskip2 pt} \exp \ln \left|\dfrac{P}{b - P}\right| & = \exp (b k t + b C) \cr \noalign{\vskip2 pt} \left|\dfrac{P}{b - P}\right| & = e^{b C}e^{b k t} \cr}$$

I can replace the $|\cdot|$ 's with a $\pm$ on the right, then set $C_0 = \pm e^{b C}$ . This yields

$$\dfrac{P}{b - P} = C_0 e^{b k t}.$$

Now some routine algebra gives

$$P = \dfrac{b C_0 e^{b k t}}{1 + C_0 e^{b k t}}.$$

Divide the top and bottom by $C_0 e^{b k t}$ , and set $C_1 = \dfrac{1}{C_0}$ :

$$P = \dfrac{b}{C_1 e^{-b k t} + 1}.$$

Suppose the initial population is $P_0$ . This means $P = P_0$ when $t = 0$ :

$$P_0 = \dfrac{b}{C_1 + 1} \quad\hbox{so}\quad C_1 = \dfrac{b}{P_0} - 1.$$

Thus, the equation is

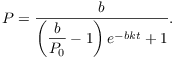
$$P = \dfrac{b}{\left(\dfrac{b}{P_0} - 1\right) e^{-b k t} + 1}.$$

For example, consider the case where $k = 1$ and $b = 3$ . I've graphed the equation for P with $P_0 = 0.2$ , 1, 2, 3, 4, and 5:

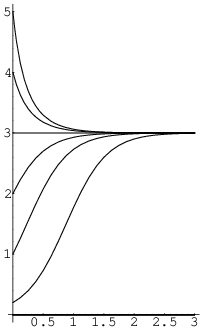
$$\hbox{\epsfysize=3in \epsffile{growth-and-decay-models-1.eps}}$$

$P_0 = 0.2$ shows initial exponential growth. As the population increases, growth levels off, approaching $P = 3$ asymptotically.

$P_0 = 1$ and $P_0 = 2$ are already large enough that the population spends most of its time levelling off, rather than growing exponentially.

An initial population $P_0 = 3$ remains constant.

$P_0 = 4$ and $P_0 = 5$ yield populations that shrink, again approaching $P = 3$ as $t \to \infty$ .

You can see why b is called the carrying capacity. Think of it as the maximum number of individuals that the environment can support. If the initial population is smaller than b, the population grows upward toward the carrying capacity. If the initial population is larger than P, individuals die and the population decreases toward the carrying capacity.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga