Implicit Differentiation

The Folium of Descartes is given by the equation $x^3 + y^3 = 3 xy$ . Picture:

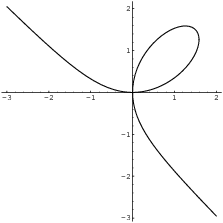
$$\hbox{\epsfysize=2in \epsffile{implicit-differentiation-1.eps}}$$

The graph consists of all points $(x,y)$ which satisfy the equation. For example, $(0,0)$ is on the graph, because $x = 0$ , $y = 0$ , satisfies the equation.

Observe, however, that the graph is not the graph of a function. Some values of x give rise to multiple values for y. (Geomtrically, this means you can draw vertical lines which hit the graph more than once.)

Moreover, it would be difficult to solve the equation for y in terms of x (unless you happen to know the general cubic formula).

However, small pieces of the graph do look like function graphs. You only need to be careful not to take a piece which is so large that it violates the vertical line criterion. For such a piece, the equation defines a function $y = f(x)$ implicitly. "Implicitly" means that y may not be solved for in terms of x, but a given x still "produces" a unique y.

On such a small piece of the graph, it would make sense to ask for the derivative $y'$ . Since it's difficult to solve for y, it's not clear how to compute the derivative.

The idea is to differentiate the equation as is, making careful use of the Chain Rule. This produces another equation, from which you can get $y'$ (perhaps implicitly as well).

Differentiate $x^3 + y^3 = 3 xy$ term-by-term with respect to x. First, the derivative of $x^3$ with respect to x is $3 x^2$ :

$$3 x^2 + \cdots $$

The derivative of $y^3$ with respect to y would be $3 y^2$ , but I'm differentiating with respect to x, so I use the Chain Rule. Differentiate the outer (cube) function, holding the inner function (y) fixed. Then differentiate the inner function. I obtain

$$3 x^2 + 3 y^2 y' = \cdots $$

Finally, differentiate the right side $3 xy$ . The 3 is constant, but $x y$ is a product: Use the Product Rule. Remember, however, that the derivative of the second factor (y) is $y'$ !

$$3 x^2 + 3 y^2 y' = 3 x y' + 3 y.$$

I can solve this equation for $\der y x$ :

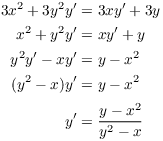
$$\eqalign{ 3 x^2 + 3 y^2 y' & = 3 x y' + 3 y \cr x^2 + y^2 y' & = x y' + y \cr y^2 y' - x y ' & = y - x^2 \cr (y^2 - x) y' & = y - x^2 \cr \noalign{\vskip2pt} y' & = \dfrac{y - x^2}{y^2 - x} \cr}$$

This may seem strange --- I've found $y'$ in terms of y --- but I can use this expression for the derivative as I normally would.

For example, I'll find the values of x where the graph has a horizontal tangent. As usual, set $y' = 0$ . I get $y - x^2 = 0$ , so $y = x^2$ . Plug this back into the original equation (because I'm looking for points on this curve):

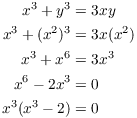
$$\eqalign{ x^3 + y^3 & = 3 x y \cr x^3 + (x^2)^3 & = 3 x (x^2) \cr x^3 + x^6 & = 3 x^3 \cr x^6 - 2 x^3 & = 0 \cr x^3 (x^3 - 2) & = 0 \cr}$$

Therefore, $x = 0$ or $x = {\root 3 \of 2}$ .

Example. Find the equation of the tangent line to

$$x^2 + 5 x = 10 y^3 + 4 y + 33 \quad\hbox{at the point}\quad (4, 1).$$

Differentiate the equation implicitly:

$$2 x + 5 = 30 y^2 y' + 4 y'.$$

Since I have a point to plug in, I don't solve this equation for $y'$ . Instead, I plug the point in first, then solve for $y'$ . Set $x = 4$ and $y = 1$ :

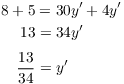
$$\eqalign{ 8 + 5 & = 30 y' + 4 y' \cr 13 & = 34 y' \cr \noalign{\vskip2pt} \dfrac{13}{34} & = y' \cr}$$

The tangent line is

$$y - 1 = \dfrac{13}{34} (x - 4), \quad\hbox{or}\quad y = \dfrac{13}{34} x - \dfrac{9}{17}.\quad\halmos$$

You can see that the rule of thumb is: To differentiate a y-expression, differentiate it "like usual", but tack on a $y'$ . The $y'$ comes from the Chain Rule. Thus:

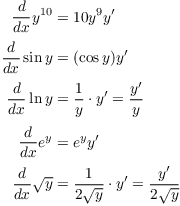
$$\eqalign{ \der {} x y^{10} & = 10 y^9 y' \cr \noalign{\vskip2pt} \der {} x \sin y & = (\cos y) y' \cr \noalign{\vskip2pt} \der {} x \ln y & = \dfrac{1}{y} \cdot y' = \dfrac{y'}{y} \cr \noalign{\vskip2pt} \der {} x e^y & = e^y y' \cr \noalign{\vskip2pt} \der {} x \sqrt{y} & = \dfrac{1}{2 \sqrt{y}} \cdot y' = \dfrac{y'}{2 \sqrt{y}} \cr}$$

Example. Find the equation of the tangent line to

$$x^3 y^2 + 4 y = 7 x + y^2 + 1 \quad\hbox{at the point}\quad (1, 2).$$

Differentiate implicitly:

$$3 x^2 y^2 + x^3 (2 y y') + 4 y' = 7 + 2 y y'.$$

Set $x = 1$ and $y = 2$ and solve for $y'$ :

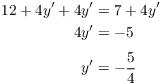
$$\eqalign{ 12 + 4 y' + 4 y' & = 7 + 4 y' \cr 4 y' & = -5 \cr \noalign{\vskip2pt} y' & = -\dfrac{5}{4} \cr}$$

The tangent line is

$$y - 2 = - \dfrac{5}{4} (x - 1), \quad\hbox{or}\quad y = -\dfrac{5}{4} x + \dfrac{13}{4}.\quad\halmos$$

Example. Find the equation of the tangent line to

$$\dfrac{y}{x} + 2 x^2 + 5 x = 3 - y^3 \quad\hbox{at the point}\quad (-1,2).$$

Differentiate implicitly:

$$\dfrac{x y' - y}{x^2} + 4 x + 5 = -3 y^2 y'.$$

Set $x = -1$ and $y = 2$ and solve for $y'$ :

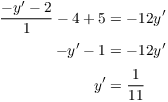
$$\eqalign{ \dfrac{-y' - 2}{1} - 4 + 5 & = -12 y' \cr \noalign{\vskip2pt} -y' - 1 & = -12 y' \cr \noalign{\vskip2pt} y' & = \dfrac{1}{11} \cr}$$

Therefore, the tangent line is

$$y - 2 = \dfrac{1}{11}(x + 1), \quad\hbox{or}\quad y = \dfrac{1}{11} x + \dfrac{23}{11}.\quad\halmos$$

Example. Find the equation of the tangent line to

$$(x + 2 y)^2 + 2 y^3 = x^3 + 20 y - 8 \quad\hbox{at the point}\quad (3,-1).$$

Differentiate implicitly:

$$2(x + 2 y)(1 + 2 y') + 6 y^2 y' = 3 x^2 + 20 y'.$$

Set $x = 3$ and $y = -1$ and solve for $y'$ :

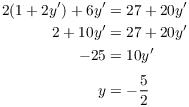
$$\eqalign{ 2(1 + 2 y') + 6 y' & = 27 + 20 y' \cr 2 + 10 y' & = 27 + 20 y' \cr -25 & = 10 y' \cr \noalign{\vskip2pt} y & = -\dfrac{5}{2} \cr}$$

Therefore, the tangent line is

$$y + 1 = -\dfrac{5}{2}(x - 3), \quad\hbox{or}\quad y = -\dfrac{5}{2} x + \dfrac{13}{2}.\quad\halmos$$

Example. Find the points on the following curve where the tangent line is horizontal:

$$y^2 - 2 y = x^4 - 32 x + 96.$$

Differentiate implicitly:

$$2 y y' - 2 y' = 4 x^3 - 32.$$

I want the horizontal tangents, so set $y' = 0$ and solve for x:

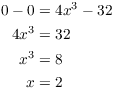
$$\eqalign{ 0 - 0 & = 4 x^3 - 32 \cr 4 x^3 & = 32 \cr x^3 & = 8 \cr x & = 2 \cr}$$

To get the y-coordinates, plug $x = 2$ into the original equation and solve for y:

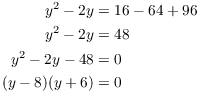
$$\eqalign{ y^2 - 2 y & = 16 - 64 + 96 \cr y^2 - 2 y & = 48 \cr y^2 - 2 y - 48 & = 0 \cr (y - 8)(y + 6) & = 0 \cr}$$

This gives $y = 8$ and $y = -6$ .

The points are $(2, 8)$ and $(2, -6)$ .

Example. The inverse tangent function $\tan^{-1} x$ satisfies

$$\tan (\tan^{-1} p) = p, \quad -\infty < p < \infty,$$

$$\tan^{-1} (\tan q) = q, \quad -\dfrac{\pi}{2} < q < \dfrac{\pi}{2}.$$

It is the inverse function to the tangent function: roughly, a function which "undoes" the effect of the tangent function.

Use implicit differentiation to compute the derivative of $y = \tan^{-1} x$ .

Start with $y = \tan^{-1} x$ and take the tangent of both sides: $\tan y = x$ . Now differentiate implicitly:

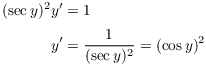
$$\eqalign{ (\sec y)^2 y' & = 1 \cr \noalign{\vskip2pt} y' & = \dfrac{1}{(\sec y)^2} = (\cos y)^2 \cr}$$

I want to express the right side in terms of x. Now $\tan y = x$ means that I have the following triangle:

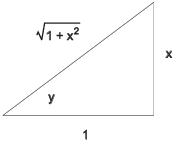
$$\hbox{\epsfysize=1.25in \epsffile{implicit-differentiation-2.eps}}$$

Therefore, $\cos y = \dfrac{1}{\sqrt{1 + x^2}}$ , and $(\cos y)^2 = \dfrac{1}{1 + x^2}$ . Hence,

$$\der {} x \tan^{-1} x = \dfrac{1}{1 + x^2}.\quad\halmos$$

Example. Find $y''$ at $(1, 1)$ for

$$x + y^3 = x^3 + 7 y - 6.$$

First, I'll differentiate implicitly and find $y'$ . Then I'll differentiate implicitly a second time to find $y''$ .

Differentiate implicitly:

$$1 + 3 y^2 y' = 3 x^2 + 7 y' \eqno{(*)}$$

Plug in $x = 1$ and $y = 1$ and solve for $y'$ :

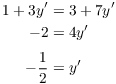
$$\eqalign{ 1 + 3 y' & = 3 + 7 y' \cr -2 & = 4 y' \cr \noalign{\vskip2 pt} -\dfrac{1}{2} & = y' \cr}$$

Next, differentiate (*) implicitly:

$$3 y^2 y'' + 6 y (y')^2 = 6 x + 7 y''.$$

Note that I used the Product Rule to differentiate the term $3 y^2 y'$ .

Now plug in $x = 1$ , $y = 1$ , and $y' = -\dfrac{1}{2}$ and solve for $y''$ :

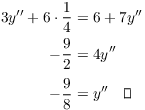
$$\eqalign{ 3 y'' + 6 \cdot \dfrac{1}{4} & = 6 + 7 y'' \cr -\dfrac{9}{2} & = 4 y'' \cr \noalign{\vskip2 pt} -\dfrac{9}{8} & = y'' \quad\halmos \cr}$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga