Increasing and Decreasing Functions

A function f (strictly) increases on a interval if $f(a) < f(b)$ whenever $a < b$ and a and b are points in the interval. This means that the graph goes up from left to right.

A function f (strictly) decreases on a interval if $f(a) > f(b)$ whenever $a < b$ and a and b are points in the interval. This means that the graph goes down from left to right.

The Mean Value Theorem can be used to tell when a function increases and when it decreases.

If $f(x)$ is a differentiable function on an interval $a < x < b$ , then:

1. f increases on $a < x < b$ if $f'(x) > 0$ on $a < x < b$ .

2. f decreases on $a < x < b$ if $f'(x) < 0$ on $a < x < b$ .

This makes sense, since the derivative gives the slope of the tangent line to the graph. Positive slope means the graph goes up from left to right and negative slope means the graph goes down from left to right.

In this way, I can use the derivative to obtain information about the shape of the graph. As an added benefit, I can tell whether a critical point is a local max or a local min.

Example. Find the intervals on which $y = 2 x^3 + 3 x^2 - 72 x + 12$ increases and the intervals on which it decreases. Locate and classify any local extrema. Sketch the graph.

The derivative is

$$y' = 6 x^2 + 6 x - 72 = 6(x + 4)(x - 3).$$

$y'$ is defined for all x, and $y' = 0$ for $x = -4$ and $x = 3$ . I set up a sign chart for $y'$ using the critical points as the break points. On each interval determined by the critical points, I pick a point at random and plug it into $y'$ .

If a point gives a positive value for $y'$ , then I know that $y'$ is positive on the interval, and hence that the function increases. I put a "+" above the interval and draw an upward-sloping line below it.

Likewise, if a point gives a negative value for $y'$ , then I know that $y'$ is negative on the interval, and hence that the function decreases. I put a "-" above the interval and draw an downward-sloping line below it.

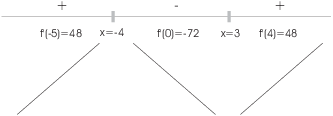
$$\hbox{\epsfxsize=3in \epsffile{increasing-decreasing-1.eps}}$$

Reading my sign chart, I see that the function increases for $x \le -4$ and for $x \ge 3$ . It decreases for $-4 \le x \le 3$ .

The upward and downward lines give a schematic picture of the graph of the function. Notice the shape of the graph at $x = -4$ : It shows that $x = -4$ is a local max.

Likewise, the shape of the schematic shows that $x = 3$ is a local min.

The use of $y'$ to classify a critical point as a max or a min is often called the First Derivative Test. By drawing a schematic picture with upward and downward lines, you remove the need to memorize the test: You can see from the schematic picture whether a point is a max or a min. Here is the statement of the test.

Theorem. ( First Derivative Test) Suppose f is continuous on an interval $a \le x \le b$ . Suppose $a < c < b$ and c is a critical point of f.

(a) If f increases to the left of c and decreases to the right of c, then c is a local max.

(b) If f decreases to the left of c and increases to the right of c, then c is a local min.

I won't give a proof, but you can see why this makes sense by drawing a sign chart for the intervals on either side of c.

Example. Find the intervals on which $y = -\dfrac{9}{4}\dfrac{1}{x^4} + \dfrac{1}{2 x^2}$ increases and the intervals on which it decreases. Locate and classify any local extrema.

The derivative is

$$y' = \dfrac{9}{x^5} - \dfrac{1}{x^3} = \dfrac{9}{x^5} - \dfrac{1}{x^3} \cdot \dfrac{x^2}{x^2} = \dfrac{9}{x^5} - \dfrac{x^2}{x^5} = \dfrac{9 - x^2}{x^5} = \dfrac{(3 - x)(3 + x)}{x^5}.$$

People often have trouble getting derivatives like these into the right form. Here's a general procedure for derivatives with fractions or negative powers:

(a) Write negative powers of x as fractions. Don't use roots for fractional powers --- it's confusing.

(b) Combine fractions over a common denominator. You want the derivative in "one chunk".

(c) Factor anything that can be factored (e.g. the top and bottom of a resulting fraction).

If the derivative is a fraction, it will equal 0 when the top is 0 and it will be undefined when the bottom is 0. (There may be other undefined places if you have things like roots or logs, of course.)

In this case, $y'$ is undefined at $x = 0$ ; this is not a critical point (because y isn't defined at $x = 0$ ), but it counts as a break point on my sign chart. The break points on your sign chart include all points where $y' = 0$ or where $y'$ is undefined, regardless of whether the function is defined at those points. Finally, $y' = 0$ for $x = \pm 3$ .

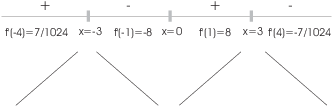
$$\hbox{\epsfxsize=3in \epsffile{increasing-decreasing-2.eps}}$$

The function increases for $x \le -3$ and for $0 < x \le 3$ . It decreases for $-3 \le x < 0$ and for $x \ge 3$ .

$x = -3$ is a local max and $x = 3$ is a local min.

Example. Find the intervals on which $y = \dfrac{3}{7}x^{7/3} - 12 x^{1/3}$ increases and the intervals on which it decreases. Locate and classify any local extrema.

The derivative is

$$y' = x^{4/3} - 4 x^{-2/3} = x^{4/3} - \dfrac{4}{x^{2/3}} = x^{4/3} \cdot \dfrac{x^{2/3}}{x^{2/3}} - \dfrac{4}{x^{2/3}} = \dfrac{x^2}{x^{2/3}} - \dfrac{4}{x^{2/3}} = \dfrac{x^2 - 4}{x^{2/3}} = \dfrac{(x - 2)(x + 2)}{x^{2/3}}.$$

$y'$ is undefined at $x = 0$ ; since y is defined at $x = 0$ , this is a critical point. $y' = 0$ for $x = \pm 2$ .

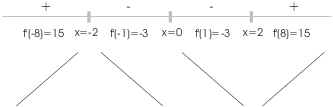
$$\hbox{\epsfxsize=3in \epsffile{increasing-decreasing-3.eps}}$$

The function increases for $x \le -2$ and for $x \ge 2$ . It decreases for $-2 \le x \le 2$ .

$x = -2$ is a local max, $x = 2$ is a local min, and $x = 0$ is neither a max nor a min.

Example. Find the intervals on which $y = \dfrac{x^2 + 1}{x^2 - 1}$ increases and the intervals on which it decreases. Locate and classify any local extrema.

You can compute the derivative using the Quotient Rule --- I'll let you do the work. The derivative is

$$y' = \dfrac{-4 x}{(x^2 - 1)^2}.$$

$y'$ is undefined for $x = \pm 1$ ; since y is also undefined for $x = \pm 1$ , these aren't critical points, though they are break points for my sign chart. $y' = 0$ for $x = 0$ .

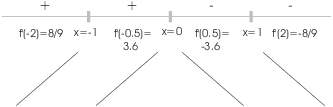
$$\hbox{\epsfxsize=3in \epsffile{increasing-decreasing-4.eps}}$$

The function increases for $x < -1$ and for $-1 < x \le 0$ . It decreases for $0 \le x < 1$ and for $x > 1$ .

$x = 0$ is a local max.

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga