Inverse Functions

Functions $f: X \to Y$ and $g: Y \to X$ are inverses if for all $x \in X$ and $y \in Y$ ,

$$f(g(y)) = y \quad\quad\hbox{and}\quad\quad g(f(x)) = x.$$

If f has an inverse, it is often denoted $f^{-1}$ . However, $f^{-1}$ does not mean "$\dfrac{1}{f}$ "!

Example. Show that $f(x) = x^3$ and $g(x) = x^{1/3}$ are inverses.

$$f(g(x)) = f(x^{1/3}) = (x^{1/3})^3 = x \quad\quad\hbox{and}\quad\quad g(f(x)) = g(x^3) = (x^3)^{1/3} = x.$$

Notice that the inverse of $f(x) = x^3$ is not $\dfrac{1}{x^3}$ !

Example. Suppose f and $f^{-1}$ are inverses and $f(4) = 17$ . What is $f^{-1}(17)$ ?

$$f(4) = 17 \quad\hbox{implies}\quad f^{-1}(17) = 4.\quad\halmos$$

Example. Let $y = f(x) = x^3 + 5$ . Find $f^{-1}(x)$ .

First, switch x's and y's:

$$x = y^3 + 5.$$

Solve for y in terms of x. The result is $f^{-1}$ :

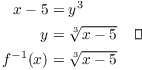
$$\eqalign{ x - 5 & = y^3 \cr y & = {\root 3 \of {x - 5}} \cr f^{-1}(x) & = {\root 3 \of {x - 5}} \cr}\quad\halmos$$

Since the inverse $f^{-1}(x)$ is obtained from $y = f(x)$ by swapping x's and y's, the graph of $f^{-1}$ is a mirror image of the graph of f across the line $y = x$ :

$$\hbox{\epsfysize=2in \epsffile{inverse-functions1.eps}}$$

Not every function has an inverse. For example, consider $f(x) = x^2$ . Now $f(2) = 4$ , so $f^{-1}$ should take 4 back to 2. But $f(-2) = 4$ as well, so apparently $f^{-1}$ should take 4 to -2. $f^{-1}$ can't do both, so there is no inverse! The problem is that you can't undo the effect of the squaring function in a unique way.

On the other hand, if I restrict $f(x) = x^2$ to $x \ge 0$ , then it has an inverse function: $f^{-1} = \sqrt{x}$ .

A function f is one-to-one or injective if different inputs go to different outputs:

$$x \ne y \quad\hbox{implies}\quad f(x) \ne f(y).$$

A graph of a function represents a one-to-one function if every horizontal line hits the graph at most once.

$$\hbox{\epsfysize=2.5in \epsffile{inverse-functions2.eps}}$$

A one-to-one function has an inverse: Since a given output could have only come from one input, you can undo the effect of the function.

Calculus provides an easy way of telling when a function is one-to-one, and hence when a function has an inverse.

Definition. A function is (strictly) increasing if

$$a < b \quad\hbox{implies}\quad f(a) < f(b).$$

That is, bigger inputs give bigger outputs.

A function is (strictly) decreasing if

$$a < b \quad\hbox{implies}\quad f(a) < f(b).$$

That is, bigger inputs give smaller outputs.

A function which is (strictly) increasing on an interval is one-to-one, (and therefore has an inverse). A function which is (strictly) decreasing on an interval is one-to-one (and therefore has an inverse).

For example, suppose f is increasing on an interval, a and b are points in the interval, and $a \ne b$ . One of the two is larger; suppose $a < b$ . Then $f(a) < f(b)$ . In particular, $f(a) \ne f(b)$ . Therefore, f is one-to-one, and has an inverse.

A similar argument works if f is decreasing.

We'll see later that a differentiable function increases on an interval if its derivative is positive, and decreases on an interval if its derivative is negative. This will give us an easy way of telling where a function has an inverse.

Example. Let $f(x) = \dfrac{1}{x^2 + 1}$ . Show that f has an inverse for $(-\infty,0]$ or $[0,+\infty)$ .

I have

$$f'(x) = \dfrac{-2x}{(x^2 + 1)^2}.$$

$f'(x) > 0$ for $x < 0$ and $f'(x) < 0$ for $x > 0$ . So f increases for $x < 0$ and decreases for $x > 0$ .

It follows that f is one-to-one (and has an inverse) on $(-\infty,0]$ or on $[0,+\infty)$ .

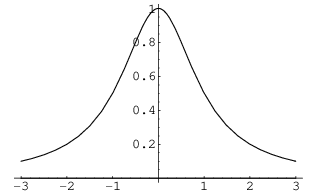
$$\hbox{\epsfysize=1.75in \epsffile{inverse-functions3.eps}}$$

As you can see, either the left half of the graph or the right half of the graph would pass the horizontal line test. But the whole graph does not.

Theorem. Suppose f is differentiable and either strictly increasing or strictly decreasing on an interval $(a, b)$ . Suppose $a < x < b$ , $f'(x) \ne 0$ , and $f(x) = y$ . Then $f^{-1}$ is differentiable at y, and

$$(f^{-1})'(y) = \dfrac{1}{f'(x)} = \dfrac{1}{f'(f^{-1}(y))}.$$

Proof. Since f is either strictly increasing or strictly decreasing on an interval $(a, b)$ , $f^{-1}$ exists and is defined on the interval $(f(a), f(b))$ , Suppose $t \in (a, b)$ and $f(t) = z \in (f(a), f(b))$ . Then

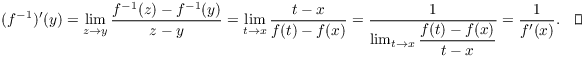
$$(f^{-1})'(y) = \lim_{z \to y} \dfrac{f^{-1}(z) - f^{-1}(y)}{z - y} = \lim_{t \to x} \dfrac{t - x}{f(t) - f(x)} = \dfrac{1}{\lim_{t \to x} \dfrac{f(t) - f(x)}{t - x}} = \dfrac{1}{f'(x)}.\quad\halmos$$

Example. The inverse sine function satisfies

$$\sin^{-1} (\sin x) = x \quad\hbox{for all}\quad x,$$

$$\sin (\sin^{-1} x) = x \quad\hbox{for}\quad -1 \le x \le 1.$$

Derive the formula for $\der {} x \sin^{-1} x$ .

The derivative of $y = \sin^{-1} x$ is

$$\der {} x \sin^{-1}(x) = \dfrac{1}{\cos(\sin^{-1}(x))}.$$

Let $\theta = \sin^{-1} x$ . Then $\sin \theta = x$ :

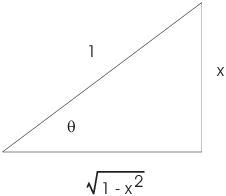
$$\hbox{\epsfysize=1.75in \epsffile{inverse-functions4.eps}}$$

Thus, $\cos(\sin^{-1}(x)) = \sqrt{1 - x^2}$ , so

$$\der {} x \sin^{-1}(x) = \dfrac{1}{\sqrt{1 - x^2}}.\quad\halmos$$

Example. If $f(3) = 5$ and $f'(3) = 7$ , find $(f^{-1})'(5)$ .

$$(f^{-1})'(5) = \dfrac{1}{f'(f^{-1}(5))} = \dfrac{1}{f'(3)} = \dfrac{1}{7}.\quad\halmos$$

Example. Suppose $f(x) = x^3$ , so $f^{-1}(x) = x^{1/3}$ . Differentiating directly,

$$\der {} x f^{-1}(x) = \dfrac{1}{3}x^{-2/3}.$$

Confirm this using the formula for the derivative of the inverse.

To use the formula for the derivative of the inverse, note that $f'(x) = 3x^2$ . Therefore,

$$\der {} x f^{-1}(x) = \dfrac{1}{f'(f^{-1}(x))} = \dfrac{1}{f'(x^{1/3})} = \dfrac{1}{3(x^{1/3})^2} = \dfrac{1}{3x^{2/3}}.$$

The results are the same.

Example. Suppose that $f(1) = 9$ and $f'(x) = \dfrac{x^2 + 5}{7x^2 + 17}$ . Find $(f^{-1})'(9)$ .

Since $f(1) = 9$ , $f^{-1}(9) = 1$ . So

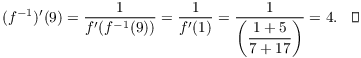
$$(f^{-1})'(9) = \dfrac{1}{f'(f^{-1}(9))} = \dfrac{1}{f'(1)} = \dfrac{1}{\left(\dfrac{1 + 5}{7 + 17}\right)} = 4.\quad\halmos$$

Example. Let $f(x) = x^6 + 5x^4 + 2$ . Notice that $f(1) = 8$ . Find $(f^{-1})'(8)$ .

First, $f'(x) = 6x^5 + 20x^3$ . Then

$$(f^{-1})'(8) = \dfrac{1}{f'(f^{-1}(8))} = \dfrac{1}{f'(1)} = \dfrac{1}{6 + 20} = \dfrac{1}{26}.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga