Inverse Trig Functions

If you restrict $f(x) = \sin x$ to the interval $-\dfrac{\pi}{2} \le x \le \dfrac{\pi}{2}$ , the function increases:

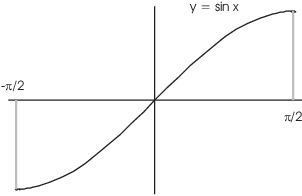
$\hbox{\epsfysize=1.75in \epsffile{inverse-trig-functions-1.eps}}$

This implies that the function is one-to-one, and hence it has an inverse. The inverse is called the inverse sine or arcsine function, and is denoted $\arcsin x$ or $\sin^{-1}(x)$ . Note that in the second case $\sin^{-1}(x)$ does not mean " $\dfrac{1}{\sin x}$ "!

Note: "Arcsine" (and $\arcsin x$ ) are older terms, and there is similar terminology for the other inverse trig functions (so "arctangent" and $\arctan x$ for the inverse tangent function, and so on). I'll use the inverse function terminology instead.

In word, $y = \sin^{-1} x$ is the angle whose sine is x. Another way of saying this is:

$y = \sin^{-1} x \quad\hbox{is the same as}\quad \sin y = x.$

The fact that $\sin$ and $\sin^{-1}$ are inverse functions can be expressed by the following equations:

$\sin \sin^{-1} a = a \quad\hbox{for}\quad -1 \le a \le 1,$

$\sin^{-1} \sin b = b \quad\hbox{for}\quad -\dfrac{\pi}{2} \le b \le \dfrac{\pi}{2}.$

Since the restricted $\sin$ takes angles in the range $-\dfrac{\pi}{2} \le x \le \dfrac{\pi}{2}$ and produces numbers in the range $-1 \le y \le 1$ , $\sin^{-1}$ takes numbers in the range $-1 \le y \le 1$ and produces angles in the range $-\dfrac{\pi}{2} \le x \le \dfrac{\pi}{2}$ .

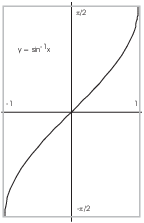
$\hbox{\epsfysize=2in \epsffile{inverse-trig-functions-2.eps}}$

Example. Compute $\sin^{-1} \dfrac{1}{2}$ and $\sin^{-1} (-1)$ .

$\sin^{-1} \dfrac{1}{2} = \dfrac{\pi}{6}, \quad\hbox{since}\quad \sin \dfrac{\pi}{6} = \dfrac{1}{2}.$

$\sin^{-1} (-1) = -\dfrac{\pi}{2}, \quad\hbox{since}\quad \sin \left(-\dfrac{\pi}{2}\right) = -1.$

Sine and arcsine are inverses, so they undo one another --- but you have to be careful!

$\sin \left(\arcsin \dfrac{2}{5}\right) = \dfrac{2}{5}, \quad\hbox{but}\quad \arcsin \left(\sin 2\pi\right) = 0, \quad\hbox{not}\quad 2\pi.$

$\sin^{-1} (\hbox{stuff})$ can't be $2\pi$ , because $\sin^{-1}$ always returns an angle in the range $-\dfrac{\pi}{2} \le x \le \dfrac{\pi}{2}$ .

Example. Find $\tan \sin^{-1} \dfrac{5}{13}$ .

First, let $\theta = \sin^{-1} \dfrac{5}{13}$ . This means that $\sin \theta = \dfrac{5}{13}$ . Now $\sin \theta = \dfrac{\rm opposite}{\rm hypotenuse}$ , so I get the following picture:

$\hbox{\epsfysize=1.5in \epsffile{inverse-trig-functions-3.eps}}$

I got the adjacent side using Pythagoras: $\sqrt{13^2 - 5^2} = 12$ .

Using the triangle, I have

$\tan \sin^{-1} \dfrac{5}{13} = \tan \theta = \dfrac{5}{12}.\quad\halmos$

You can find a derivative formula for $\sin^{-1}$ using implicit differentiation. Let $y = \sin^{-1} x$ . This is equivalent to $x = \sin y$ . Differentiate implicitly:

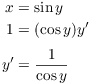
$\eqalign{ x & = \sin y \cr 1 & = (\cos y) y' \cr \noalign{\vskip2pt} y' & = \dfrac{1}{\cos y} \cr}$

I'd like to express the result in terms of x. Here's the right triangle that says $x = \sin y$ :

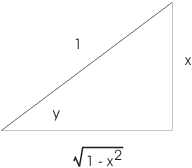
$\hbox{\epsfysize=1.5in \epsffile{inverse-trig-functions-4.eps}}$

I found the other leg using Pythagoras. You can see that $\cos y = \sqrt{1 - x^2}$ . Hence, $y' = \dfrac{1}{\sqrt{1 - x^2}}$ . That is,

$\der {} x \sin^{-1} x = \dfrac{1}{\sqrt{1 - x^2}}.$

Every derivative formula gives rise to a corresponding antiderivative formula:

$\int \dfrac{1}{\sqrt{1 - x^2}}\,dx = \sin^{-1} x + C.$

Before I do some calculus examples, I want to mention some of the other inverse trig functions. I'll discuss the inverse cosine, inverse tangent, and inverse secant functions.

(a) You get the inverse cosine by inverting $\cos x$ , restricted to $0 \le x \le \pi$ .

$\hbox{\epsfysize=2in \epsffile{inverse-trig-functions-5.eps}}$

(b) You get the inverse tangent by inverting $\tan x$ , restricted to $-\dfrac{\pi}{2} < x < \dfrac{\pi}{2}$ .

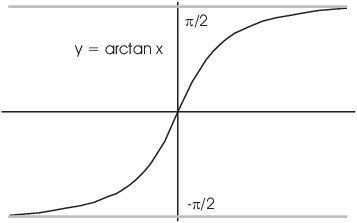
$\hbox{\epsfysize=2in \epsffile{inverse-trig-functions-6.eps}}$

(c) You get the inverse secant by inverting $\sec x$ , restricted to $0 < x < \dfrac{\pi}{2}$ together with $\dfrac{\pi}{2} < x < \pi$ .

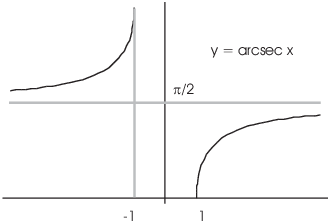
$\hbox{\epsfysize=2in \epsffile{inverse-trig-functions-7.eps}}$

As with $\sin$ and $\sin^{-1}$ , the domains and ranges of these functions and their inverses are "swapped":

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & Function & & Domain & & Range & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $\sin^{-1}$ & & $-1 \le x \le 1$ & & $-\dfrac{\pi}{2} \le x \le \dfrac{\pi}{2}$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $\cos^{-1}$ & & $-1 \le x \le 1$ & & $0 \le x \le \pi$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $\tan^{-1}$ & & $-\infty < x < \infty$ & & $-\dfrac{\pi}{2} < x < \dfrac{\pi}{2}$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $\sec^{-1}$ & & $x \le -1, x \ge 1$ & & $0 \le x < \dfrac{\pi}{2}, \dfrac{\pi}{2} < x \le \pi$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

Example. Compute $\tan^{-1} 1$ and $\cos^{-1} \left(-\dfrac{1}{2}\right)$ .

$\tan^{-1} 1 = \dfrac{\pi}{4}, \quad\hbox{since}\quad \tan \dfrac{\pi}{4} = 1.$

$\cos^{-1} \left(-\dfrac{1}{2}\right) = \dfrac{2\pi}{3}, \quad\hbox{since}\quad \cos \dfrac{2\pi}{3} = -\dfrac{1}{2}.\quad\halmos$

You can derive the derivative formulas for the other inverse trig functions using implicit differentiation, just as I did for the inverse sine function.

$\der {} x \cos^{-1} x = -\dfrac{1}{\sqrt{1 - x^2}}$

$\der {} x \tan^{-1} x = \dfrac{1}{1 + x^2}$

$\der {} x \sec^{-1} x = \dfrac{1}{|x|\sqrt{x^2 - 1}}$

For example, I'll derive the formula for $\der {} x \sec^{-1} x$ .

The derivation starts out like the derivation for $\der {} x \sin^{-1} x$ . Let $y = \sec^{-1} x$ , so $\sec y = x$ . Differentiating implicitly, I get

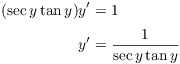
$\eqalign{ (\sec y \tan y) y' & = 1 \cr \noalign{\vskip2pt} y' & = \dfrac{1}{\sec y \tan y} \cr}$

There are two cases, depending on whether $x \ge 1$ or $x \le -1$ .

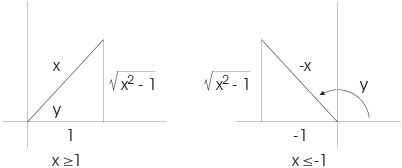
$\hbox{\epsfysize=1.5in \epsffile{inverse-trig-functions-8.eps}}$

Suppose $x \ge 1$ . Then $y = \sec^{-1} x$ is in the interval $0 \le y < \dfrac{\pi}{2}$ , as illustrated in the first diagram above. You can see from the picture that

$\sec y = x \quad\hbox{and}\quad \tan y = \sqrt{x^2 - 1}.$

Therefore,

$y' = \dfrac{1}{\sec y \tan y} = \dfrac{1}{x \sqrt{x^2 - 1}}.$

$x \ge 1$ , so x is positive, and . Therefore,

$y' = \dfrac{1}{x \sqrt{x^2 - 1}} = \dfrac{1}{|x| \sqrt{x^2 - 1}}.$

Now suppose that $x \le -1$ . Then $y = \sec^{-1} x$ is in the interval $\dfrac{\pi}{2} < y \le \pi$ , as illustrated in the second diagram above. Since x is negative, the hypotenuse must be , since it must be positive and since $\sec y = \dfrac{(\hbox{hypotenuse})}{(\hbox{adjacent})}$ must equal x. In this case,

$\sec y = x \quad\hbox{and}\quad \tan y = -\sqrt{x^2 - 1}.$

Therefore,

$y' = \dfrac{1}{\sec y \tan y} = \dfrac{1}{-x \sqrt{x^2 - 1}}.$

$x \le -1$ , so x is negative, and . Therefore,

$y' = \dfrac{1}{-x \sqrt{x^2 - 1}} = \dfrac{1}{|x| \sqrt{x^2 - 1}}.$

This proves that $y' = \dfrac{1}{|x|\sqrt{x^2 - 1}}$ in all cases.

Example. Compute:

(a) $\displaystyle \der {} x \left(\sin^{-1} \sqrt{x} + \sqrt{\sin^{-1} x}\right)$ .

(b) $\displaystyle \der {} x \dfrac{1}{\tan^{-1} x}$ .

(a)

$\der {} x \left(\sin^{-1} \sqrt{x} + \sqrt{\sin^{-1} x}\right) = \dfrac{1}{\sqrt{1 - x}}\cdot \dfrac{1}{2 \sqrt{x}} + \dfrac{1}{2} \left(\sin^{-1} x\right)^{-1/2} \cdot \dfrac{1}{\sqrt{1 - x^2}}.\quad\halmos$

(b)

$\der {} x \dfrac{1}{\tan^{-1} x} = \left(-\dfrac{1}{(\tan^{-1} x)^2}\right) \left(\dfrac{1}{1 + x^2}\right).\quad\halmos$

(c)

$\der {} x \sec^{-1} (e^x) = \dfrac{e^x}{e^x \sqrt{e^{2x} - 1}} = \dfrac{1}{\sqrt{e^{2x} - 1}}.\quad\halmos$

I don't need absolute values in the last example, because is always positive.

Example. Prove the identity

$\tan^{-1} w + \tan^{-1} \dfrac{1}{w} = \dfrac{\pi}{2}.$

$\der {} x \tan^{-1} \dfrac{1}{w} = \dfrac{-\dfrac{1}{w^2}}{1 + \dfrac{1}{w^2}} = -\dfrac{1}{1 + w^2}.$

Hence,

$\der {} x \left(\tan^{-1} w + \tan^{-1} \dfrac{1}{w}\right) = 0.$

A function with zero derivative is constant, so

$\tan^{-1} w + \tan^{-1} \dfrac{1}{w} = C, \quad\hbox{a constant}.$

But when ,

$C = \tan^{-1} w + \tan^{-1} \dfrac{1}{w} = \tan^{-1} 1 + \tan^{-1} 1 = \dfrac{\pi}{2}.$

Therefore,

$\tan^{-1} w + \tan^{-1} \dfrac{1}{w} = \dfrac{\pi}{2}.\quad\halmos$

Here are the integration formulas for some of the inverse trig functions. I'm giving extended versions of the formulas --- with " " replacing the "1" that you'd get if you just reversed the derivative formulas --- in order to save you a little time in doing problems.

$\int \dfrac{1}{\sqrt{a^2 - x^2}}\,dx = \sin^{-1} \dfrac{x}{a} + C$

$\int \dfrac{1}{a^2 + x^2}\,dx = \dfrac{1}{a} \tan^{-1} \dfrac{x}{a} + C$

$\int \dfrac{1}{|x|\sqrt{x^2 - a^2}}\,dx = \dfrac{1}{a} \sec^{-1} \dfrac{x}{a} + C$

For instance, here's how to derive the extended $\sin^{-1}$ integral formula from the formula $\displaystyle \int \dfrac{1}{\sqrt{1 - x^2}}\,dx = \sin^{-1} x + C$ using substitution:

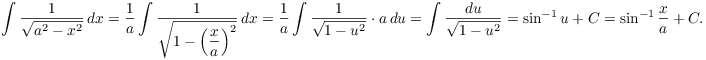
$\int \dfrac{1}{\sqrt{a^2 - x^2}}\,dx = \dfrac{1}{a} \int \dfrac{1} {\sqrt{1 - \left(\dfrac{x}{a}\right)^2}}\,dx = \dfrac{1}{a} \int \dfrac{1}{\sqrt{1 - u^2}}\cdot a\,du = \int \dfrac{du}{\sqrt{1 - u^2}} = \sin^{-1} u + C = \sin^{-1} \dfrac{x}{a} + C.$

$\left[u = \dfrac{x}{a}, \quad du = \dfrac{dx}{a}, \quad dx = a\,du\right]$

Example. Compute $\displaystyle \int \dfrac{dx}{4 + x^2}$ and $\displaystyle \int \dfrac{1}{\sqrt{3 - x^2}}\,dx$ .

Using the $\tan^{-1}$ formula with ,

$\int \dfrac{dx}{4 + x^2} = \dfrac{1}{2} \tan^{-1} \dfrac{x}{2} + C.$

Using the $\sin^{-1}$ formula with $a = \sqrt{3}$ ,

$\int \dfrac{1}{\sqrt{3 - x^2}}\,dx = \sin^{-1} \dfrac{x}{\sqrt{3}} + C.\quad\halmos$

Example. Compute $\displaystyle \int \dfrac{dx}{1 + 4x^2}$ .

$\int \dfrac{dx}{1 + 4 x^2} = \int \dfrac{dx}{1 + (2 x)^2} = \int \dfrac{1}{1 + u^2}\cdot \dfrac{du}{2} = \dfrac{1}{2} \tan^{-1} u + C = \dfrac{1}{2} \tan^{-1} (2 x) + C.$

$\left[u = 2 x, \quad du = 2\,dx, \quad dx = \dfrac{du}{2}\right]\quad\halmos$

Example. Compute $\displaystyle \int \dfrac{x^4\,dx}{1 + x^{10}}$ .

$\int \dfrac{x^4\,dx}{1 + x^{10}} = \int \dfrac{x^4\,dx}{1 + (x^5)^2} = \int \dfrac{x^4}{1 + u^2}\cdot \dfrac{du}{5 x^4} = \dfrac{1}{5} \int \dfrac{du}{1 + u^2} =$

$\left[u = x^5, \quad du = 5 x^4\,dx, \quad dx = \dfrac{du}{5 x^4}\right]$

$\dfrac{1}{5} \tan^{-1} u + C = \dfrac{1}{5} \tan^{-1} (x^5) + C.\quad\halmos$

Example. Compute $\displaystyle \int \dfrac{e^x}{\sqrt{1 - e^{2x}}}\,dx$ .

$\int \dfrac{e^x}{\sqrt{1 - e^{2x}}}\,dx = \int \dfrac{e^x}{\sqrt{1 - u^2}}\cdot \dfrac{du}{e^x} = \int \dfrac{du}{\sqrt{1 - u^2}} = \sin^{-1} u + C = \sin^{-1} e^x + C.$

$\left[u = e^x, \quad du = e^x\,dx, \quad dx = \dfrac{du}{e^x}\right]\quad\halmos$

Example. Compute $\displaystyle \int \dfrac{(\sec x)^2\,dx}{\sqrt{1 - (\tan x)^2}}$ .

$\int \dfrac{(\sec x)^2\,dx}{\sqrt{1 - (\tan x)^2}} = \int \dfrac{(\sec x)^2}{\sqrt{1 - u^2}}\cdot \dfrac{du}{(\sec x)^2} = \int \dfrac{du}{\sqrt{1 - u^2}} = \sin^{-1} u + C = \sin^{-1} \tan x + C.$

$\left[u = \tan x, \quad du = (\sec x)^2\,dx, \quad dx = \dfrac{du}{(\sec x)^2}\right]\quad\halmos$

Contact information

Bruce Ikenaga's Home Page