In some cases, you let x approach the number a from the left or the right, rather than "both sides at once" as usual.
1. ![]() means: Compute the
limit of
means: Compute the
limit of ![]() as x approaches c from the right
--- that is, through numbers bigger than c.
as x approaches c from the right
--- that is, through numbers bigger than c.
2. ![]() means: Compute the
limit of
means: Compute the
limit of ![]() as x approaches c from the left
--- that is, through numbers smaller than c.
as x approaches c from the left
--- that is, through numbers smaller than c.
These situations may occur if ![]() is only defined to
the left or to the right of c. For example, the function
is only defined to
the left or to the right of c. For example, the function ![]() is only defined for
is only defined for ![]() (because the square root of a negative number is not
a real number).
(because the square root of a negative number is not
a real number).
It's also possible to consider left and right-hand limits when ![]() is defined on both sides of c. In this case, the
important question is: Are the left and right-hand limits equal?
is defined on both sides of c. In this case, the
important question is: Are the left and right-hand limits equal?
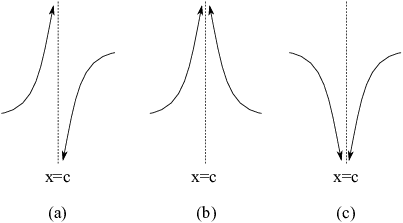
Example. The pictures show the graphs of some functions. In each case, tell whether the left and right-hand limits at c are defined. If both are defined, tell whether they are equal.

In (a), the right-hand limit is defined, because the graph approaches
a definite height from the right (the height of the dot). The
left-hand limit is undefined because the graph is not approaching a
definite height: There is a vertical asymptote. (You could also say
the left-hand limit is ![]() , as we'll discuss
below.)
, as we'll discuss
below.)
Likewise, in (b), the right-hand limit is undefined, and the
left-hand limit is defined. (You could also say the right-hand limit
is ![]() , as we'll discuss below.)
, as we'll discuss below.)
Finally, in (c), both the right and left-hand limits are defined, but
they aren't equal. (This means that the ordinary
("two-sided") limit ![]() is undefined.
is undefined.![]()
I won't state a lot of theorems about left and right-hand limits, because in general the results that hold for ordinary ("two-sided") limits hold for one-sided limits. For example (omitting the usual technical assumptions), here is the rule for sums for right-hand limits:
![]()
You can see that it's the same as the rule for sums for ordinary
limits, the only difference being that I'm now writing "![]() " instead of "
" instead of "![]() ".
".
One important point which we've already noted is the relationship between left and right-hand limits and ordinary ("two-sided") limits. To give a little more detail, I'll first give the formal definitions for left and right-hand limits.
Definition. (a) ( Right-hand
limits) Suppose ![]() is defined on an
interval
is defined on an
interval ![]() for
for ![]() . To say that
. To say that ![]() means: For every number
means: For every number ![]() , there is a number
, there is a number ![]() , such that
, such that
![]()
(b) ( Left-hand limits) Suppose ![]() is defined on an interval
is defined on an interval ![]() for
for ![]() . To say that
. To say that ![]() means: For every
number
means: For every
number ![]() , there is a number
, there is a number ![]() , such that
, such that
![]()
Note that in each case, ![]() might actually be
defined on both sides of c. We're saying that for the right-hand
limit to exist, it only needs to be defined to the right of
c; for the left-hand limit to exist, it only needs to be
defined to the left of c. (As usual,
might actually be
defined on both sides of c. We're saying that for the right-hand
limit to exist, it only needs to be defined to the right of
c; for the left-hand limit to exist, it only needs to be
defined to the left of c. (As usual, ![]() may or may not be defined at c.)
may or may not be defined at c.)
Here's the result which we've used informally before that relates
left and right-hand limits to ordinary ("two-sided")
limits. The proof is an ![]() proof like
the ones I gave in the sections on the definition of limits and limit
theorems; if you're in an ordinary first-term calculus course, you
can skip the proof if you wish.
proof like
the ones I gave in the sections on the definition of limits and limit
theorems; if you're in an ordinary first-term calculus course, you
can skip the proof if you wish.
Theorem. Suppose ![]() is defined on an open interval containing c.
is defined on an open interval containing c.
Then ![]() is defined
if and only if
is defined
if and only if ![]() and
and ![]() are both defined and equal.
are both defined and equal.
In this case, ![]() is equal to the common value of
is equal to the common value of ![]() and
and ![]() .
.
![]()
Proof. The proof of this theorem comes down to the following fact about absolute values:
![]()
The reason is that ![]() means that x is within
means that x is within ![]() of c, but is not
equal to c.
of c, but is not
equal to c.
On the other hand, ![]() means that x is
less than c and is within
means that x is
less than c and is within ![]() of c, and
of c, and ![]() means that x is greater than c and is
within
means that x is greater than c and is
within ![]() of c. Thus, if one of these two statements
is true, then the previous statement is true, and if the previous
statement is true, then one of these must be true.
of c. Thus, if one of these two statements
is true, then the previous statement is true, and if the previous
statement is true, then one of these must be true.
Thus, suppose ![]() . I'll show that
. I'll show that
![]()
Let ![]() . Since
. Since ![]() , there is a number
, there is a number
![]() such that if
such that if ![]() , then
, then ![]() .
.
First, if ![]() , then
, then ![]() . Consequently,
. Consequently, ![]() .
.
Second, if ![]() , then
, then ![]() . Consequently,
. Consequently, ![]() .
.
Next, I'll prove that converse. Suppose that
![]()
I'll show that
![]()
Let ![]() . Since
. Since ![]() , there's a
number
, there's a
number ![]() such that if
such that if ![]() , then
, then ![]() .
.
Likewise, since ![]() , there's a number
, there's a number ![]() such that if
such that if ![]() ,
then
,
then ![]() .
.
Now let ![]() . Remember that this means that
. Remember that this means that ![]() is the smaller of
is the smaller of ![]() and
and ![]() , so it's at
least as small as either.
, so it's at
least as small as either.
Suppose ![]() . This means that either
. This means that either
![]()
In the first case, I have
![]()
Hence, ![]() .
.
In the second case, I have
![]()
Hence, ![]() .
.
This proves that ![]() .
.![]()
In words, this result says that the ordinary ("two-sided") limit is defined if and only if the left and right-hand limits are defined and equal, and in that case, their common value is the value of the ordinary limit.
Example. Compute
![]()
Is ![]() defined?
defined?
![]()
Look at the first limit more closely. x approaches 0 from the
right. Numbers close to, but to the right of, 0 are small
positive numbers: 0.01, for example. Small positive numbers make ![]() positive:
positive: ![]() , for example. If
, for example. If ![]() is positive, then
is positive, then ![]() , so
, so
![]()
(Notice that you don't let x equal 0, so ![]() , and the cancellation is legal.)
, and the cancellation is legal.)
Therefore,
![]()
Here's the picture:
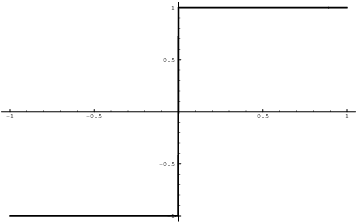
Since the left- and right-hand limits are not the same, ![]() is
undefined.
is
undefined.![]()
Example. Suppose
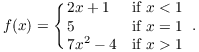
Compute ![]() ,
, ![]() , and
, and ![]() .
.
To compute ![]() , I use the
part of the definition for f which applies to
, I use the
part of the definition for f which applies to ![]() :
:
![]()
Likewise, to compute ![]() , I use the part of the definition for f which
applies to
, I use the part of the definition for f which
applies to ![]() :
:
![]()
Since the left and right-hand limits are equal, the two-sided limit
is defined, and![]() .
.
The fact that ![]() does not come into the
problem.
does not come into the
problem.![]()
Example. A function is defined by
![]()
For what value of k is ![]() defined?
defined?
In order for ![]() to be defined, the left and right-hand limits at 2
must be defined and equal. Compute them:
to be defined, the left and right-hand limits at 2
must be defined and equal. Compute them:
![]()
![]()
Set the left and right-hand limits equal and solve for k:

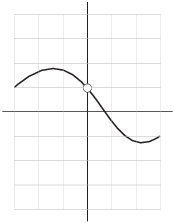
Example. Consider the function ![]() whose graph is depicted below:
whose graph is depicted below:
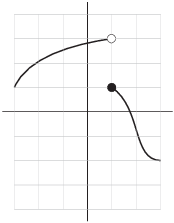
Compute ![]() .
.
Then
![]()
Since the left- and right-hand limits are not the same,
![]()
Example. Consider the function ![]() whose graph is depicted below:
whose graph is depicted below:
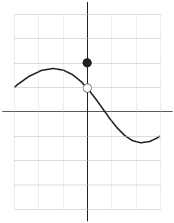
Compute
![]()
Do these limits depend on the value of ![]() ?
?
Then
![]()
Therefore,
![]()
The value of ![]() does not affect the existence of
the limit. In fact, suppose I change the function as follows:
does not affect the existence of
the limit. In fact, suppose I change the function as follows:
Now ![]() is undefined, but
is undefined, but
![]()
Left and right-hand limits can give rise to infinite limits, so I'll discuss the ideas briefly before giving some examples. As usual with the theory in this course, the precise definitions are here for the sake of completeness, and for people who are interested. For most people, it's enough that you have a good grasp of how it looks graphically when a limit is infinite, and how infinite limits can arise in limit computations.
Definition. (a) ![]() means: For every
number
means: For every
number ![]() , there is a number
, there is a number ![]() , such that if
, such that if ![]() , then
, then ![]() .
.
Sometimes I'll write "![]() " instead of
"
" instead of
"![]() " for emphasis, to help distinguish it
from "
" for emphasis, to help distinguish it
from "![]() " in the next part of the
definition.
" in the next part of the
definition.
The definitions for right and left-hand limits are:
(i) (Right-hand limits) ![]() means: For every number
means: For every number ![]() , there is a number
, there is a number ![]() , such that if
, such that if ![]() , then
, then ![]() .
.
(ii) (Left-hand limits) ![]() means: For every number
means: For every number ![]() , there is a number
, there is a number ![]() , such that if
, such that if ![]() , then
, then ![]() .
.
(b) ![]() means: For every number
means: For every number ![]() , there is a number
, there is a number
![]() , such that if
, such that if ![]() , then
, then ![]() .
.
The definitions for right and left-hand limits are:
(i) (Right-hand limits) ![]() means: For every number
means: For every number ![]() , there is a number
, there is a number ![]() , such that if
, such that if ![]() , then
, then ![]() .
.
(ii) (Left-hand limits) ![]() means: For every number
means: For every number ![]() , there is a number
, there is a number ![]() , such that if
, such that if ![]() , then
, then ![]() .
.
Thus, to say ![]() approaches
approaches ![]() as x approaches c (from the left, the right, or from
both sides) means that as
as x approaches c (from the left, the right, or from
both sides) means that as ![]() becomes larger and
positive, without any upper bound, as x approaches c.
becomes larger and
positive, without any upper bound, as x approaches c.
Likewise, to say ![]() approaches
approaches ![]() as x approaches c (from the left, the right, or from
both sides) means that as
as x approaches c (from the left, the right, or from
both sides) means that as ![]() becomes larger and
negative, without any upper bound, as x approaches c.
becomes larger and
negative, without any upper bound, as x approaches c.
In all of these cases, it would not be wrong to say that the limit is
undefined, in the sense that it is not a number. But if you
can say it is ![]() or
or ![]() , it is better, since you're giving more information
about what is happening.
, it is better, since you're giving more information
about what is happening.
Example. Each picture below shows the graph of
a function ![]() . In each case, find:
. In each case, find:
![]()
In (a),
![]()
Since the left and right-hand limits do not agree, ![]() is undefined.
is undefined.
In (b),
![]()
![]()
Example. Compute ![]() .
.
Plugging in gives ![]() . The limit
is undefined. But I can say more.
. The limit
is undefined. But I can say more.
Try plugging in a number close to 1: When ![]() ,
,
![]()
It looks as though ![]() is getting big and negative. In fact,
is getting big and negative. In fact,
![]()
To why this is true, remember that x is approaching 1 from the
right. This means that ![]() will be small and
positive. On the other hand,
will be small and
positive. On the other hand, ![]() .
Since the top is negative and the bottom is positive, the result must
be negative.
.
Since the top is negative and the bottom is positive, the result must
be negative.
As far as size goes, I have
![]()
Since the result should be big and negative, it is
reasonable that it is ![]() .
.
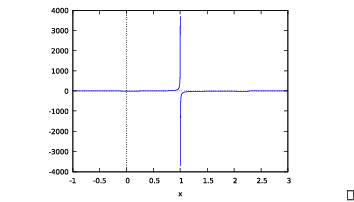
Another way to see this is to draw the graph near ![]() . As you move toward 1 from the right, the graph goes
downward toward
. As you move toward 1 from the right, the graph goes
downward toward ![]() .
.
I noted the following fact earlier: Suppose
![]()
Then the two-sided limit ![]() is undefined. As the example above
shows, the situation is different with one-sided limits.
is undefined. As the example above
shows, the situation is different with one-sided limits.
If in this situation ![]() has the same
sign for all x's sufficiently close to c and greater than c,
then the right-hand limit
has the same
sign for all x's sufficiently close to c and greater than c,
then the right-hand limit ![]() will be either
will be either ![]() or
or ![]() . The specific
sign depends on the signs of the top and the bottom of the fraction.
. The specific
sign depends on the signs of the top and the bottom of the fraction.
Likewise, if ![]() has the same sign for all
x's sufficiently close to c and less than c, then the left-hand limit
has the same sign for all
x's sufficiently close to c and less than c, then the left-hand limit
![]() will be either
will be either ![]() or
or ![]() . Again, the
specific sign depends on the signs of the top and the bottom of the
fraction.
. Again, the
specific sign depends on the signs of the top and the bottom of the
fraction.
The "same-sign" condition will be satisfied, for example,
if f and g are polynomials --- that is, if ![]() is a rational function. It will
also be satisfied by functions like
is a rational function. It will
also be satisfied by functions like
![]()
Example. Compute ![]() .
.
Plugging ![]() in gives
in gives ![]() . Since
. Since ![]() is a rational function, the
right-hand limit
is a rational function, the
right-hand limit ![]() is either
is either ![]() or
or ![]() ; I have to
determine which of the two it is. I'll look at the top and the bottom
separately.
; I have to
determine which of the two it is. I'll look at the top and the bottom
separately.
As ![]() ,
, ![]() .
.
As for the bottom, since x is approaching -3 from the right,
I'm considering x's greater than -3. Thus, ![]() , so
, so ![]() ---
--- ![]() is positive.
is positive.
Since ![]() is approaching a negative number and
is approaching a negative number and ![]() is approaching a positive number, the quotient is
negative. Therefore,
is approaching a positive number, the quotient is
negative. Therefore,
![]()
I can also see this if I take a number close to -3 but to the right
of -3 --- ![]() , for example --- and plug it in:
, for example --- and plug it in:
![]()
I got a large negative number, which suggests that the limit
should be ![]() .
.
I could also see this by graphing the function, as in the previous example.
In the case of a one-sided limit and a form ![]() , you might ask:
"Which of these methods is the best to determine the
value?" I feel that for a first course in calculus, all three
are acceptable.
, you might ask:
"Which of these methods is the best to determine the
value?" I feel that for a first course in calculus, all three
are acceptable.
However, while plugging in numbers and drawing graphs provide support for a conclusion, they don't really provide a proof. Graphs can be deceiving. And when you plug in a number, how do you know that the number you chose is "typical"? The first method --- reasoning about signs using inequalities --- is much closer to a rigorous proof of the result.
Copyright 2018 by Bruce Ikenaga