L'Hôpital's Rule

L'Hôpital's Rule is a method for computing a limit of the form

$$\lim_{x \to c} \dfrac{f(x)}{g(x)}.$$

c can be a number, $+\infty$ , or $-\infty$ . The conditions for applying it are:

1. The functions f and g are differentiable in an open interval containing c. (c may also be an endpoint of the open interval, if the limit is one-sided.)

2. g and $g'$ are nonzero in the open interval, except possibly at c.

3. $\displaystyle \lim_{x \to c} \dfrac{f'(x)}{g'(x)}$ is defined, or is $+\infty$ , or is $-\infty$ .

4. As $x \to c$ ,

$$\dfrac{f(x)}{g(x)} \to \dfrac{0}{0} \quad\quad\hbox{or}\quad\quad \dfrac{\infty}{\infty}.$$

If these conditions hold, then

$$\lim_{x \to c} \dfrac{f(x)}{g(x)} = \lim_{x \to c} \dfrac{f'(x)}{g'(x)}.$$

In other words, f and g may be replaced by their derivatives.

Note that you're not applying the Quotient Rule to $\dfrac{f(x)}{g(x)}$ .

A proof may be given using some advanced results (e.g. the Extended Mean Value Theorem). I won't give a proof here.

Example. Compute

$$\lim_{x \to 1} \dfrac{4 x^{100} - x - 3}{5 x^{50} - x - 4}.$$

Plugging $x = 1$ into $\dfrac{4 x^{100} - x - 3}{5 x^{50} - x - 4}$ gives $\dfrac{0}{0}$ , so I can apply L'Hôpital's Rule:

$$\lim_{x \to 1} \dfrac{4 x^{100} - x - 3}{5 x^{50} - x - 4} = \lim_{x \to 1} \dfrac{400 x^{99} - 1}{250 x^{49} - 1} = \dfrac{400 - 1}{250 - 1} = \dfrac{399}{249}.\quad\halmos$$

Example. Compute

$$\lim_{x \to 2} \dfrac{\sin (x^2 - 4)}{x - 2}.$$

Plugging $x = 2$ into $\dfrac{\sin (x^2 - 4)}{x - 2}$ gives $\dfrac{0}{0}$ , so I can apply L'Hôpital's Rule:

$$\lim_{x \to 2} \dfrac{\sin (x^2 - 4)}{x - 2} = \lim_{x \to 2} \dfrac{2 x \cos (x^2 - 4)}{1} = 4.\quad\halmos$$

Example. Compute

$$\lim_{x \to +\infty} \dfrac{\ln (x - 4)}{x}.$$

As $x \to +\infty$ , $\dfrac{\ln (x - 4)}{x} \to \dfrac{\infty}{\infty}$ , so I can apply L'Hôpital's Rule:

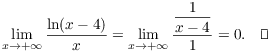
$$\lim_{x \to +\infty} \dfrac{\ln (x - 4)}{x} = \lim_{x \to +\infty} \dfrac{\dfrac{1}{x - 4}}{1} = 0.\quad\halmos$$

Example. Compute

$$\lim_{x \to 0^+} \dfrac{x^2 + 3 x + 7}{x}.$$

As $x \to 0^+$ , $\dfrac{x^2 + 3 x + 7}{x} \to \dfrac{7}{0}$ , so I can't apply L'Hôpital's Rule. In fact, since the top and bottom are both positive,

$$\lim_{x \to 0^+} \dfrac{x^2 + 3 x + 7}{x} = +\infty.\quad\halmos$$

Example. Compute

$$\lim_{x \to \infty} \left(\sqrt{x^2 + 6 x} - x\right).$$

As $x \to +\infty$ , $\sqrt{x^2 + 6 x} - x \to \infty - \infty$ (which is not 0!). I convert the expression into a fraction by rationalizing:

$$\lim_{x \to \infty} \left(\sqrt{x^2 + 6 x} - x\right) = \lim_{x \to \infty} \left(\sqrt{x^2 + 6 x} - x\right)\cdot \dfrac{\sqrt{x^2 + 6 x} + x}{\sqrt{x^2 + 6 x} + x} = \lim_{x \to \infty} \dfrac{x^2 + 6 x - x^2}{\sqrt{x^2 + 6 x} + x} = \lim_{x \to \infty} \dfrac{6 x}{\sqrt{x^2 + 6 x} + x}.$$

As $x \to +\infty$ , $\dfrac{6 x}{\sqrt{x^2 + 6 x} + x} \to \dfrac{\infty}{\infty}$ , so I could apply L'Hôpital's Rule. Instead, I'll divide the top and bottom by x:

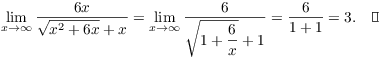
$$\lim_{x \to \infty} \dfrac{6 x}{\sqrt{x^2 + 6 x} + x} = \lim_{x \to \infty} \dfrac{6}{\sqrt{1 + \dfrac{6}{x}} + 1} = \dfrac{6}{1 + 1} = 3.\quad\halmos$$

If you apply L'Hôpital's Rule, and the limit you obtain is undefined, you may not conclude that the original limit is undefined.

Example. Compute

$$\lim_{x \to \infty} \dfrac{x - \sin x}{x + \sin x}.$$

As $x \to +\infty$ , $\dfrac{x - \sin x}{x + \sin x} \to {\infty}{\infty}$ , so I can apply L'Hôpital's Rule:

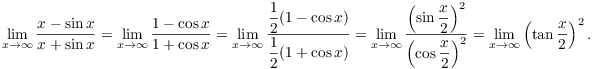
$$\lim_{x \to \infty} \dfrac{x - \sin x}{x + \sin x} = \lim_{x \to \infty} \dfrac{1 - \cos x}{1 + \cos x} = \lim_{x \to \infty} \dfrac{\dfrac{1}{2}(1 - \cos x)}{\dfrac{1}{2}(1 + \cos x)} = \lim_{x \to \infty} \dfrac{\left(\sin \dfrac{x}{2}\right)^2} {\left(\cos \dfrac{x}{2}\right)^2} = \lim_{x \to \infty} \left(\tan \dfrac{x}{2}\right)^2.$$

The last limit is undefined, because $\tan \dfrac{x}{2}$ has no limit as $x \to \infty$ . This implies that the $=$ 's in the reasoning above aren't valid. When you do a L'Hôpital computation, the equalities are actually provisional, pending the existence of a limit in the chain.

In fact, the original limit exists:

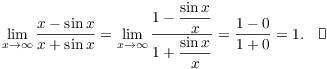
$$\lim_{x \to \infty} \dfrac{x - \sin x}{x + \sin x} = \lim_{x \to \infty} \dfrac{1 - \dfrac{\sin x}{x}} {1 + \dfrac{\sin x}{x}} = \dfrac{1 - 0}{1 + 0} = 1.\quad\halmos$$

You can handle the indeterminate form $0 \cdot \infty$ by using algebra to convert the expression to a fraction, and then applying L'Hôpital's Rule.

Example. Compute

$$\lim_{x \to \pi/2^-} \left(x - \dfrac{\pi}{2}\right)\tan x.$$

As $x \to \pi/2^-$ , $\left(x - \dfrac{\pi}{2}\right)\tan x \to 0 \cdot \infty$ . So

$$\lim_{x \to \pi/2^-} \left(x - \dfrac{\pi}{2}\right)\tan x = \lim_{x \to \pi/2^-} \dfrac{x - \dfrac{\pi}{2}}{\cot x}.$$

As $x \to \pi/2^-$ , $\dfrac{x - \dfrac{\pi}{2}}{\cot x} \to \dfrac{0}{0}$ , so I can apply L'Hôpital's Rule:

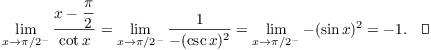
$$\lim_{x \to \pi/2^-} \dfrac{x - \dfrac{\pi}{2}}{\cot x} = \lim_{x \to \pi/2^-} \dfrac{1}{-(\csc x)^2} = \lim_{x \to \pi/2^-} -(\sin x)^2 = -1.\quad\halmos$$

The indeterminate form $1^\infty$ can be handled by taking logs, computing the limit using the techniques above, and finally exponentiating to undo the log.

Example. Compute

$$\lim_{x \to \infty} \left(1 + \dfrac{3}{x}\right)^{5 x}.$$

As $x \to \infty$ , $\left(1 + \dfrac{3}{x}\right)^{5 x} \to 1^\infty$ .

Let $y = \left(1 + \dfrac{3}{x}\right)^{5 x}$ . Then

$$\ln y = \ln \left(1 + \dfrac{3}{x}\right)^{5 x} = 5 x \ln \left(1 + \dfrac{3}{x}\right).$$

So

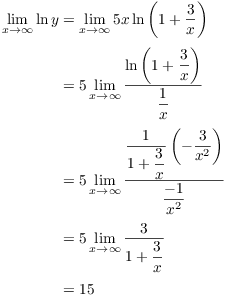
$$\eqalign{ \lim_{x \to \infty} \ln y & = \lim_{x \to \infty} 5 x \ln \left(1 + \dfrac{3}{x}\right) \cr \noalign{\vskip2pt} & = 5 \lim_{x \to \infty} \dfrac{\ln \left(1 + \dfrac{3}{x}\right)}{\dfrac{1}{x}} \cr \noalign{\vskip2pt} & = 5 \lim_{x \to \infty} \dfrac{\dfrac{1}{1 + \dfrac{3}{x}} \left(-\dfrac{3}{x^2}\right)}{\dfrac{-1}{x^2}} \cr \noalign{\vskip2pt} & = 5 \lim_{x \to \infty} \dfrac{3}{1 + \dfrac{3}{x}} \cr \noalign{\vskip2pt} & = 15 \cr}$$

Therefore,

$$\lim_{x \to \infty} \left(1 + \dfrac{3}{x}\right)^{5 x} = e^{15}.\quad\halmos$$

Example. Compute

$$\lim_{x \to \infty} \left(\dfrac{x + 1}{x - 2}\right)^{2 x - 1}.$$

As $x \to \infty$ , $\left(\dfrac{x + 1}{x - 2}\right)^{2 x - 1} \to 1^\infty$ .

Let $y = \left(\dfrac{x + 1}{x - 2}\right)^{2 x - 1}$ . Then

$$\ln y = \ln \left(\dfrac{x + 1}{x - 2}\right)^{2 x - 1} = (2 x - 1) \ln \left(\dfrac{x + 1}{x - 2}\right).$$

So

$$\lim_{x \to \infty} \ln y = \lim_{x \to \infty} (2 x - 1) \ln \left(\dfrac{x + 1}{x - 2}\right).$$

As $x \to \infty$ , $(2 x - 1) \ln \left(\dfrac{x + 1}{x - 2}\right) \to \infty \cdot 0$ . So convert the expression to a fraction:

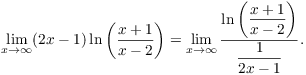
$$\lim_{x \to \infty} (2 x - 1) \ln \left(\dfrac{x + 1}{x - 2}\right) = \lim_{x \to \infty} \dfrac{\ln \left(\dfrac{x + 1}{x - 2}\right)} {\dfrac{1}{2 x - 1}}.$$

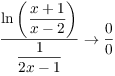As $x \to \infty$ , $\dfrac{\ln \left(\dfrac{x + 1}{x - 2}\right)}{\dfrac{1}{2 x - 1}} \to \dfrac{0}{0}$ , so I can apply L'Hôpital's Rule:

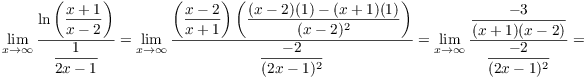
$$\lim_{x \to \infty} \dfrac{\ln \left(\dfrac{x + 1}{x - 2}\right)} {\dfrac{1}{2 x - 1}} = \lim_{x \to \infty} \dfrac{\left(\dfrac{x - 2}{x + 1}\right) \left(\dfrac{(x - 2)(1) - (x + 1)(1)}{(x - 2)^2}\right)} {\dfrac{-2}{(2 x - 1)^2}} = \lim_{x \to \infty} \dfrac{\dfrac{-3}{(x + 1)(x - 2)}} {\dfrac{-2}{(2 x - 1)^2}} =$$

$$\dfrac{3}{2} \lim_{x \to \infty} \dfrac{(2 x - 1)^2}{(x + 1)(x - 2)} = 6.$$

That is, $\lim_{x \to \infty} \ln y = 6$ . Therefore,

$$\lim_{x \to \infty} y = e^{(\lim_{x \to \infty} \ln y)} = e^6 = 403.42879 \ldots.\quad\halmos$$

Example. Compute $\displaystyle \lim_{x \to 1^+} \left(\tan \dfrac{\pi x}{4}\right)^{3/(x - 1)}$ .

As $x \to 1^+$ , $\left(\tan \dfrac{\pi x}{4}\right)^{3/(x - 1)} \to 1^\infty$ . Set $y = \left(\tan \dfrac{\pi x}{4}\right)^{3/(x - 1)}$ . Take logs and simplify:

$$\ln y = \ln \left(\tan \dfrac{\pi x}{4}\right)^{3/(x - 1)} = 3 \cdot \dfrac{\ln \left(\tan \dfrac{\pi x}{4}\right)}{x - 1}.$$

Take the limit as $x \to 1^+$ , applying L'Hôpital's rule to the fraction:

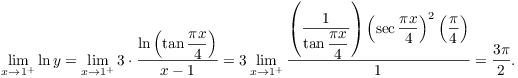
$$\lim_{x \to 1^+} \ln y = \lim_{x \to 1^+} 3 \cdot \dfrac{\ln \left(\tan \dfrac{\pi x}{4}\right)}{x - 1} = 3 \lim_{x \to 1^+} \dfrac{\left(\dfrac{1} {\tan \dfrac{\pi x}{4}}\right)\left(\sec \dfrac{\pi x}{4}\right)^2 \left(\dfrac{\pi}{4}\right)}{1} = \dfrac{3\pi}{2}.$$

Hence, $\displaystyle \lim_{x \to 1^+} \left(\tan \dfrac{\pi x}{4}\right)^{3/(x - 1)} = e^{3 \pi/2}$ .

Example. Compute $\displaystyle \lim_{x \to 1} \left(\dfrac{x}{x - 1} - \dfrac{1}{\ln x}\right)$ .

This is an indeterminate form $\dfrac{1}{0} - \dfrac{1}{0}$ . Combine the fractions over a common denominator:

$$\lim_{x \to 1} \left(\dfrac{x}{x - 1} - \dfrac{1}{\ln x}\right) = \lim_{x \to 1} \dfrac{x\ln x - (x - 1)}{(x - 1)\ln x} = \lim_{x \to 1} \dfrac{x\ln x - x + 1)}{(x - 1)\ln x}.$$

This is an $\dfrac{0}{0}$ form, so I can apply L'Hôpital's Rule:

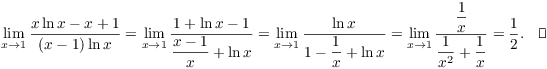
$$\lim_{x \to 1} \dfrac{x\ln x - x + 1}{(x - 1)\ln x} = \lim_{x \to 1} \dfrac{1 + \ln x - 1}{\dfrac{x - 1}{x} + \ln x} = \lim_{x \to 1} \dfrac{\ln x}{1 - \dfrac{1}{x} + \ln x} = \lim_{x \to 1} \dfrac{\dfrac{1}{x}}{\dfrac{1}{x^2} + \dfrac{1}{x}} = \dfrac{1}{2}.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga