Having discussed how you can compute limits, I want to examine the definition of a limit in more detail.
You might wonder why it is necessary to be careful. Suppose you're
trying to compute ![]() . You might think of drawing a
graph; many graphing calculators, for instance, produce a graph like
the one below:
. You might think of drawing a
graph; many graphing calculators, for instance, produce a graph like
the one below:
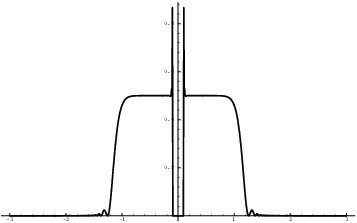
It looks as though the graph is dropping down to 0 near ![]() . From this, you might guess that the limit is 0. In
fact,
. From this, you might guess that the limit is 0. In
fact,
![]()
It's possible to justify this algebraically once you know a little about limits of trig functions.
Pictures can be helpful; so can experimenting with numbers. In many cases, pictures and numerical experiments are inconclusive or even misleading. In these cases, how can you determine whether a proposed answer is correct or not?
Because the limit definition is a bit abstract, I'll start off with an informal definition.
Informal Definition. If ![]() can be made arbitrarily close to L for all x's
sufficiently close to c, then
can be made arbitrarily close to L for all x's
sufficiently close to c, then
![]()
This statement is like a guarantee. Think of making parts in a factory. Your customers won't buy your parts unless they meet certain specifications. So you might guarantee that your parts will be within 0.01 of the customer's specification.
Likewise, to say that ![]() you must be able to guarantee that you can make
you must be able to guarantee that you can make ![]() fall within (say) 0.01 of L. But you have to do more:
You have to be able to make
fall within (say) 0.01 of L. But you have to do more:
You have to be able to make ![]() fall within any
positive tolerance of L --- 0.0001, 0.0000004, and so on, no
matter how small.
fall within any
positive tolerance of L --- 0.0001, 0.0000004, and so on, no
matter how small.
Another way to think of this is as meeting a challenge; for example:
Challenge: "I challenge you to make ![]() stay within 0.0005 of L."
stay within 0.0005 of L."
Your response: "I guarantee that every x
within 0.003 of c (except perhaps c itself) will give an ![]() that is within 0.0005 of L."
that is within 0.0005 of L."
To prove that ![]() , you
must be able to meet the challenge no matter what positive
number is used in place of 0.0005.
, you
must be able to meet the challenge no matter what positive
number is used in place of 0.0005.
By the way, notice that ![]() is excluded in my guarantee.
The reason is that in computing
is excluded in my guarantee.
The reason is that in computing ![]() , we're concerned with what happens as x
approaches c, not what
, we're concerned with what happens as x
approaches c, not what ![]() is.
is.
Before I give some examples, here's an important fact about absolute value:
![]()
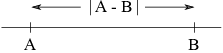
We want absolute values, which are always nonnegative, because a distance shouldn't be negative.
Also, notice that
![]()
That makes sense, because the distance from A to B should be the same as the distance from B to A. For instance,
![]()
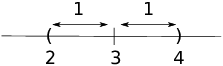
Example. By plugging in ![]() , it appears that
, it appears that
![]()
How close should x be to 4 to guarantee that ![]() is within 0.01 of 7?
is within 0.01 of 7?
Let's work backwards: I want ![]() to be within 0.01
of 7. This means
to be within 0.01
of 7. This means
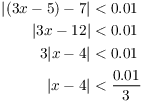
The last inequality says that the distance from x to 4 should be less
than ![]() . So if x lies within
. So if x lies within ![]() of 4, I can guarantee that
of 4, I can guarantee that ![]() will be within 0.01 of 7.
will be within 0.01 of 7.
A formal proof would just reverse the steps above:
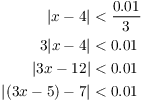
Can you see that if I'm challenged to make ![]() lie within 0.00001 of 7, I should make x lie within
lie within 0.00001 of 7, I should make x lie within
![]() of 4? Just replace 0.01 with 0.00001 in the
discussion above.
of 4? Just replace 0.01 with 0.00001 in the
discussion above.
And similarly, I can make ![]() lie within any tolerance FOO
of 7 by making x lie within
lie within any tolerance FOO
of 7 by making x lie within ![]() of
4.
of
4.
This shows that I can meet any challenge, since I can just take the challenge tolerance and plug it in for FOO. This proves that
![]()
Example. The graph of a function ![]() is shown below.
is shown below.
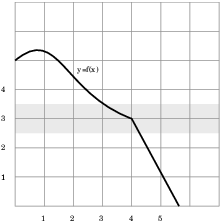
It appears that ![]() .
.
A (grey) horizontal strip of width 0.5 is drawn around ![]() . Draw a picture to show a range of x-values around 4
for which the corresponding
. Draw a picture to show a range of x-values around 4
for which the corresponding ![]() -values lie in the
horizontal strip.
-values lie in the
horizontal strip.
Use it to estimate the width of a symmetric vertical strip around 4
representing x-values whose corresponding ![]() -values lie in the horizontal strip.
-values lie in the horizontal strip.
Suppose I'm challenged to make ![]() fall within 0.5 of 3.
That is, I want my y-values to fall within the grey strip in the
picture.
fall within 0.5 of 3.
That is, I want my y-values to fall within the grey strip in the
picture.
On the right side of 4, the graph stays within the grey strip as far as 4.25; on the left side of 4, the graph stays within the grey strip as far as 3.
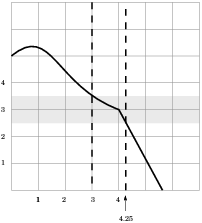
If I want a strip that's symmetric about 4, I use the closer of the
two values, which is 4.25. Now 4.25 is 0.25 units from 4, so my
answer is: If x is within 0.25 of 4, then ![]() will be within 0.5 of 3.
will be within 0.5 of 3.![]()
If I can meet such a challenge with any positive number in
place of 0.5, then I will have proved that ![]() .
.
Example. (Disproving a limit) Consider the
function ![]() whose graph is show below.
whose graph is show below.
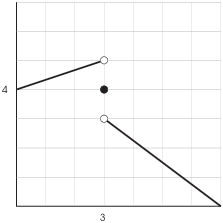
Suppose that Calvin Butterball thinks that ![]() . Use the limit definition
to disprove it.
. Use the limit definition
to disprove it.
To disprove Calvin's claim, I'll make a challenge that Calvin can't meet.
I challenge Calvin to make ![]() fall within 0.5 of 4.
This means that he must find a range of x's around 3 so that the
corresponding part of the graph lies within the grey strip shown
below:
fall within 0.5 of 4.
This means that he must find a range of x's around 3 so that the
corresponding part of the graph lies within the grey strip shown
below:
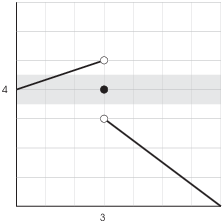
You can see that there's no way to do this. (Note: He's not allowed
to use ![]() alone. Remember that what the function does
at
alone. Remember that what the function does
at ![]() has no bearing on the value of the limit.)
has no bearing on the value of the limit.)
Since this challenge can't be met, ![]() . In fact,
. In fact, ![]() is undefined.
is undefined.![]()
Example. Suppose
![]()
It appears that ![]() . How
close should x be to 1 in order to guarantee that
. How
close should x be to 1 in order to guarantee that ![]() will be within 0.0008 of 3?
will be within 0.0008 of 3?
As in an earlier example, I'll work backwards.
From the left side, I'd need
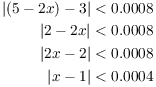
The last inequality says that x should be within 0.0004 of 1.
From the right side, I'd need
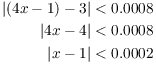
This means that x should be within 0.0002 of 1.
To satisfy the two requirements at the same time, I'll use the smaller of the two numbers. So I'll require that x should be within 0.0002 of 1, which means
![]()
Here is the "real" proof, which I get by writing the scratch work in the reverse order.
Suppose ![]() . If
. If ![]() , I have
, I have
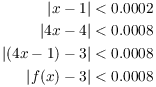
Now
![]()
So if ![]() , I have
, I have
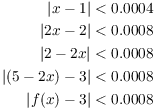
(From the second to the third line, I used the fact that ![]() .)
.)
Thus, if x is within 0.0002 of 1, then ![]() will be within 0.0008 of 3.
will be within 0.0008 of 3.![]()
I'm almost ready to give the formal definition of a limit, but I need to mention something first as a matter of honesty. It's a technical issue, and it won't arise in the majority of problems and examples (so you can ignore it without much harm if you wish).
A technical point. In discussing ![]() , I'll usually assume that
f is defined on an open interval containing c. That is, there are
numbers a and b such that
, I'll usually assume that
f is defined on an open interval containing c. That is, there are
numbers a and b such that ![]() and f is defined (at
least) on
and f is defined (at
least) on ![]() .
.
For one-sided limit (which I'll discuss later), ![]() should be defined on an open interval with c as an
endpoint.
should be defined on an open interval with c as an
endpoint.
To understand why you want to do this, consider the function
![]()
(So, for instance, f is simply not defined at ![]() , or at
, or at ![]() .)
.)
In the definition of ![]() , the "if" part of the definition would
hold vacuously (for small open intervals around -10), because there
would be no values of x near -10 for which f was defined.
Thus, the limit L could be anything!
, the "if" part of the definition would
hold vacuously (for small open intervals around -10), because there
would be no values of x near -10 for which f was defined.
Thus, the limit L could be anything!
The condition on the domain of f is made to avoid silly cases like this one.
In order to avoid cluttering the statements of the definition or of proofs of limit properties, I usually won't state this assumption about the domains of functions in limits explicitly.
Now I'll give the formal definition of a limit, and show how to use
it to do ![]() proofs.
proofs.
Definition. ![]() means:
means:
For every ![]() , there is a
, there is a ![]() , such that for all x in the domain of f, if
, such that for all x in the domain of f, if ![]() , then
, then ![]() .
.
"![]() " is the Greek letter epsilon. It is
the "challenge number", the tolerance or maximum error you
have to meet.
" is the Greek letter epsilon. It is
the "challenge number", the tolerance or maximum error you
have to meet. ![]() is the Greek letter delta. It is
the "response number", the setting on x which meets the
challenge. The Greek letters are used in this definition for
traditional reaons; there is nothing otherwise special about them.
is the Greek letter delta. It is
the "response number", the setting on x which meets the
challenge. The Greek letters are used in this definition for
traditional reaons; there is nothing otherwise special about them.
Let's see how proofs of limits work using the definition.
Example. Prove that ![]() .
.
In this problem, 4 corresponds to c, ![]() corresponds to
corresponds to ![]() , and 25 corresponds
to L in the limit definition.
, and 25 corresponds
to L in the limit definition.
I have to show that, given any ![]() , there is a
, there is a
![]() , such that
, such that
![]()
Notice that I'm given ![]() , but I'm not told
its value (which was the case in earlier examples). All I can assume
is that it's some positive number. I have to come up with a
, but I'm not told
its value (which was the case in earlier examples). All I can assume
is that it's some positive number. I have to come up with a ![]() that meets the condition above. To do this, I work
backwards as I did in earlier examples. This is
"scratchwork", and doesn't count as the "real"
proof, which will come afterward.
that meets the condition above. To do this, I work
backwards as I did in earlier examples. This is
"scratchwork", and doesn't count as the "real"
proof, which will come afterward.
Scratchwork. I want ![]() . I'll work backwards from this
and try to get something that looks like "
. I'll work backwards from this
and try to get something that looks like "![]() ". Then I'll set
". Then I'll set ![]() and try to do the real proof.
and try to do the real proof.
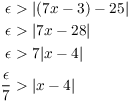
Okay --- I'll try ![]() .
.
The real proof. Let ![]() . I must show that
. I must show that
![]()
When you are proving an "if-then" statement, you get to assume the "if" part, and you prove the "then" part. So assume
![]()
The rest of the proof is easy: I just reverse the steps I did on scratchwork:
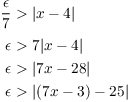
Therefore, by the limit definition,
![]()
A similar approach works for limits of the form ![]() . Here is a harder example.
. Here is a harder example.
Example. Prove that ![]() .
.
In this case, 3 corresponds to c, ![]() corresponds to
corresponds to
![]() , and 24 corresponds to L.
, and 24 corresponds to L.
Scratchwork. I want ![]() . I'll work backwards from this
and try to get something that looks like "
. I'll work backwards from this
and try to get something that looks like "![]() ". Then I'll set
". Then I'll set ![]() and try to do the real proof.
and try to do the real proof.
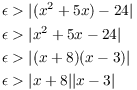
I can't just divide both sides by ![]() (like I divided by
7 in the last example:
(like I divided by
7 in the last example:
![]()
The problem is that I can't set ![]() , because I would need to know x in order to know
, because I would need to know x in order to know
![]() --- but
--- but ![]() is supposed to
determine the range of x's.
is supposed to
determine the range of x's.
Instead, I need to make a "preliminary" setting of ![]() . I'll provisionally set
. I'll provisionally set ![]() . Then
. Then
![]()
Remember that you have complete control over ![]() . Setting
. Setting ![]() to 1 is like
adjusting a setting on an instrument, where you make an initial rough
setting, then fine-tune it. We'll see how this works out when we
write the "real proof".
to 1 is like
adjusting a setting on an instrument, where you make an initial rough
setting, then fine-tune it. We'll see how this works out when we
write the "real proof".
Adding 8 to each term, I get
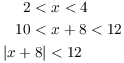
Remember that I want the inequality ![]() .
.
If I could get ![]() , then I'd have
, then I'd have
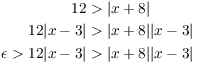
But
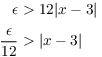
It looks like I should try ![]() ... but then, I remember I needed to set
... but then, I remember I needed to set ![]() earlier. How can I get both of these things
to happen? The idea is to make
earlier. How can I get both of these things
to happen? The idea is to make ![]() the
smaller of the two numbers 1 and
the
smaller of the two numbers 1 and ![]() --- in symbols,
--- in symbols,
![]()
("min" stands for "minimum".) This means that
![]()
The real proof. Let ![]() . I
must show that:
. I
must show that:
![]()
So I may assume ![]() ,
and I have to prove
,
and I have to prove ![]() .
.
As I noted in the scratchwork, I know that
![]()
Take ![]() first. Then
first. Then
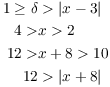
Next, I'll use ![]() . Multiply this inequality and the inequality
. Multiply this inequality and the inequality ![]() to get
to get
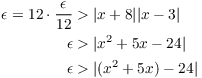
Therefore, I've proved that ![]() .
.![]()
Copyright 2018 by Bruce Ikenaga