Limit Properties

There are many rules for computing limits. I'll list the most important ones. I'll give proofs of some of these rules separately. I'm stating the most of the technical conditions required for these results to hold; if you want to see the full statements of the rules, check the section on proofs of limit properties.

There are analogous results for left and right-hand limits; just replace " $\displaystyle \lim_{x \to c}$ " with " $\displaystyle \lim_{x \to c^+}$ " or " $\displaystyle \lim_{x \to c^-}$ ".

I mentioned the first rule earlier:

1. If is a polynomial, then $\lim_{x \to c} f(x) = f(c)$ .

Remember that a polynomial is a function of the form

$a_0 + a_1 x + \cdots + a_n x^n.$

The a's are numbers. The rule says you can compute the limit of a polynomial as x goes to c by plugging c in for x.

Example. Compute $\displaystyle \lim_{x \to 1} (x^3 + 2 x + 7)$ .

$\lim_{x \to 1} (x^3 + 2 x + 7) = 1 + 2 + 7 = 10.\quad\halmos$

2. "The limit of a sum is the sum of the limits."

$\lim_{x \to a} \left(f(x) + g(x)\right) = \lim_{x \to a} f(x) + \lim_{x \to a} g(x).$

This equation --- and the ones like it that follow --- must be interpreted as follows: The statement is true provided that the two limits on the right side are defined.

Example. Suppose $\displaystyle \lim_{x \to 3} f(x) = 17$ .

Compute $\displaystyle \lim_{x \to 3} \left(f(x) + x^2\right)$ .

Using the sum rule and the polynomial rule, I have

$\lim_{x \to 3} \left(f(x) + x^2\right) = 17 + 9 = 26.\quad\halmos$

3. "The limit of a product is the product of the limits."

$\lim_{x \to a} \left(f(x)\cdot g(x)\right) = \left(\lim_{x \to a} f(x)\right) \cdot \left(\lim_{x \to a} g(x)\right).$

Again, the statement is true provided that the two limits on the right side are defined.

Example. Suppose $\displaystyle \lim_{x \to 2} f(x) = 5$ .

Compute $\displaystyle \lim_{x \to 2} (x^2 + 3) f(x)$ .

The polynomial rule gives

$\lim_{x \to 2} (x^2 + 3) = 2^2 + 3 = 7.$

The product rule gives

$\lim_{x \to 2} (x^2 + 3) f(x) = 7 \cdot 5 = 35.\quad\halmos$

Using mathematical induction and the rule for products, you can prove:

4. "The limit of a power is the power of the limit."

$\lim_{x \to a} f(x)^n = \left(\lim_{x \to a} f(x)\right)^n.$

In this equation, n is a positive integer, and the statement is true provided that $\displaystyle \lim_{x \to a} f(x)$ is defined.

Example. Suppose $\displaystyle \lim_{x \to 5} f(x) = 8$ . Compute

$\lim_{x \to 5} f(x)^3.$

$\lim_{x \to 5} f(x)^3 = 8^3 = 512.\quad\halmos$

You have to be a little careful with quotients to avoid division by zero.

5. "The limit of a quotient is the quotient of the limits" --- provided that the denominator does not become 0 when you plug in.

$\lim_{x \to a} \dfrac{f(x)}{g(x)} = \dfrac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)}, \quad\hbox{if}\quad g(a) \ne 0.$

In any case, the statement is only true if $\displaystyle \lim_{x \to a} f(x)$ and $\displaystyle \lim_{x \to a} g(x)$ are defined.

If the denominator approaches 0, there are two possibilities.

(a) If the numerator approaches a nonzero number (so you're getting " $\dfrac{(\hbox{nonzero number})}{0}$ "), the limit is undefined.

(b) If the numerator approaches 0 (so you're getting " $\dfrac{0}{0}$ "), you must do additional work to decide whether the limit is defined (and if it's defined, what its value is).

Example. Compute $\displaystyle \lim_{x \to 2} \dfrac{x^2 + 3}{2 x^3 + 7 x - 10}$ .

Using the rules for quotients and for polynomials,

$\lim_{x \to 2} \dfrac{x^2 + 3}{2 x^3 + 7 x - 10} = \dfrac{2^2 + 3}{2\cdot 2^3 + 7\cdot 2 - 10} = \dfrac{7}{20}. \quad\halmos$

As the last example shows, you can use the rules for quotients and for polynomials to compute the limit of a rational function. A rational function is a polynomial divided by a polynomial. For example, here are some rational functions:

$\dfrac{x^2 + 7}{7 x^{50} - \sqrt{2} x^3 + 3}, \quad \dfrac{5}{x^7 - 3}, \quad\hbox{and}\quad \dfrac{14 x + 1}{x - 2}.$

Example. (a) Find $\displaystyle \lim_{x \to 2} \dfrac{x^2 + 3 x - 4}{x - 2}$ .

(b) Find $\displaystyle \lim_{x \to 2} \dfrac{x^2 - 4}{x^2 + 4 x + 4}$ .

(a)

$\lim_{x \to 2} \dfrac{x^2 + 3 x - 4}{x - 2} \quad\hbox{is undefined}.$

Reason: The numerator approaches 6 (a nonzero number) while the denominator approaches 0.

(b)

$\lim_{x \to 2} \dfrac{x^2 - 4}{x^2 + 4 x + 4} = \dfrac{0}{16} = 0.$

There's nothing wrong with having 0 on the top of a fraction.

Example. Compute $\displaystyle \lim_{x \to 3} \dfrac{x^2 - 9}{x^2 - 10 x + 21}$ .

In this case, plugging in gives $\dfrac{0}{0}$ , an indeterminate form. I need to do more work to determine whether the limit is defined. Factor and cancel:

$\lim_{x \to 3} \dfrac{x^2 - 9}{x^2 - 10 x + 21} = \lim_{x \to 3} \dfrac{(x - 3)(x + 3)}{(x - 3)(x - 7)} = \lim_{x \to 3} \dfrac{x + 3}{x - 7} = \dfrac{6}{-4} = -\dfrac{3}{2}.\quad\halmos$

6. "Constants pull out of limits." If k is a number, then

$\lim_{x \to a} k \cdot f(x) = k \cdot \lim_{x \to a} f(x).$

The result is true provided that the limit on the right is defined.

Note that since a constant (by itself) is a polynomial, the polynomial rule implies that if k is a constant,

$\lim_{x \to c} k = k.$

Example. Suppose $\displaystyle \lim_{x \to 4} f(x) = 17$ . Compute

$\lim_{x \to 4} 3 \cdot f(x).$

$\lim_{x \to 4} 3 \cdot f(x) = 3 \cdot \lim_{x \to 4} f(x) = 3 \cdot 17 = 51.\quad\halmos$

7. "The limit of a root is the root of the limit."

$\lim_{x \to a} \root n \of {f(x)} = \root n \of {\lim_{x \to a} f(x)}.$

The result holds provided that $\displaystyle \lim_{x \to a} f(x)$ is defined. Moreover, n should be an odd positive integer --- or if n is an even positive integer, then $\displaystyle \lim_{x \to a} f(x)$ should be positive.

Note that the situation may be complicated if n is even and $\displaystyle \lim_{x \to a} f(x) = 0$ , as we'll see in an example.

Example. Compute $\displaystyle \lim_{x \to -1} \root 3 \of {\dfrac{x^2 - 5 x - 2}{x - 2}}$ .

Since I'm taking an odd root, it doesn't matter whether the function inside the root is approaching a positive or a negative number.

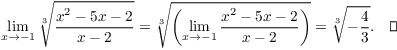
$\lim_{x \to -1} \root 3 \of {\dfrac{x^2 - 5 x - 2}{x - 2}} = \root 3 \of {\left(\lim_{x \to -1} \dfrac{x^2 - 5 x - 2}{x - 2}\right)} = \root 3 \of {-\dfrac{4}{3}}.\quad\halmos$

(You could write this as $-\root 3 \of {\dfrac{4}{3}}$ .)

Example. Compute $\displaystyle \lim_{x \to 4} \sqrt{x^2 - 5 x - 1}$ .

As $x \to 4$ , the quantity inside the square root approaches $4^2 - 5\cdot 4 - 1 = -5$ . Therefore, the limit is undefined.

Example. Compute $\displaystyle \lim_{x \to 3} \sqrt{x^2 - 9}$ .

As $x \to 3$ , I have $x^2 - 9 \to 0$ . You might think that, since $\sqrt{0} = 0$ , the limit should be 0. In fact, the limit is undefined.

To see why, remember that when x approaches 3, it does so from both sides. But what happens if x is less than 3? Suppose . Then

$x^2 - 9 = (2.9)^2 - 9 = 8.41 - 9 = -0.59, \quad\hbox{and}\quad \sqrt{x^2 - 9} = \sqrt{-0.59} \quad\hbox{is undefined}.$

In other words, x can't approach 3 from the left (through numbers less than 3) because $\sqrt{x^2 - 9}$ is undefined for . Hence, the limit is undefined.

Later on, I'll show that if x approaches 3 from the right, then the limit is indeed 0.

8. ( Trig functions, logs, and exponentials) Suppose is one of

$\sin x, \quad \cos x, \quad \tan x, \quad \cot x, \quad \sec x, \quad \csc x, \quad e^x, \quad \ln x.$

Suppose c is a number in the domain of . Then

$\lim_{x \to c} f(x) = f(c).$

9. ( Composites) Suppose that:

(a) $\displaystyle \lim_{x \to a} f(x) = b$ .

(b) $\displaystyle \lim_{x \to b} g(x) = c$ .

Then

$\lim_{x \to c} g(f(x)) = c.$

Here's an example which uses the last two rules.

Example. Compute $\displaystyle \lim_{x \to 2} \sin (x^2 + 1)$ .

By the rule for polynomials,

$\lim{x \to 2} (x^2 + 1) = 5.$

Since $\sin 5$ is defined, the rules for sine and composites give

$\lim_{x \to 2} \sin (x^2 + 1) = \sin 5.\quad\halmos$

The next result is often called the Squeeze Theorem (or the Sandwich Theorem). It is different from the other computational rules in that it produces an answer in an indirect way.

The Squeeze Theorem is an intuitively obvious result about limits. Suppose you have three functions , , , and you're trying to compute the limit of as x approaches a.

10. ( The Squeeze Theorem) Suppose you know that:

(a) $\displaystyle \lim_{x \to a} f(x) = L$ and $\lim_{x \to a} h(x) = L$ .

(b) $f(x) \le g(x) \le h(x)$ (at least for x's in some interval around a).

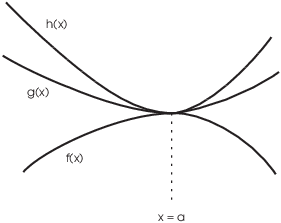
$\hbox{\epsfysize=2in \epsffile{limit-properties-1.eps}}$

Then

$\lim_{x \to a} g(x) = L.$

The result in reasonable because g is "sandwiched" between f and h.

Example. Compute $\displaystyle \lim_{x \to 0} x^2 \sin \dfrac{1}{x}$ .

As $x \to 0$ , $x^2 \to 0$ , but $\sin \dfrac{1}{x}$ oscillates. And at , $\sin \dfrac{1}{x}$ is undefined. There's no "algebraic" rule which would allow you to compute the limit, but the Squeeze Theorem makes it easy.

$\sin (\hbox{anything})$ always lies between -1 and 1:

$-1 \le \sin \dfrac{1}{x} \le 1.$

Multiply through by :

$-x^2 \le x^2 \sin \dfrac{1}{x} \le x^2.$

Note that $x^2 \ge 0$ , so the inequalities don't "flip over".

Now

$\lim_{x \to 0} (-x^2) = 0 \quad\hbox{and}\quad \lim_{x \to 0} x^2 = 0.$

Hence, by the Squeeze Theorem

$\lim_{x \to 0} x^2 \sin \dfrac{1}{x} = 0.$

The picture below shows the graphs of , , and $x^2 \sin \dfrac{1}{x}$ . Notice that $x^2 \sin \dfrac{1}{x}$ is indeed caught between the two parabolas, which squeeze the wiggly graph as $x \to 0$ :

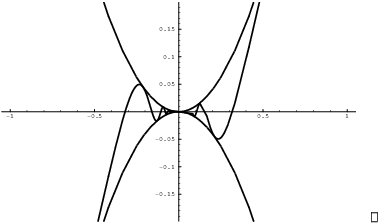
$\hbox{\epsfysize=2in \epsffile{limit-properties-2.eps}\quad\halmos}$

The next property is often not stated explicitly, but it's often used in computing limits. It gives a precise statement of the fact that $\displaystyle \lim_{x \to c} f(x)$ depends on what does near c, not what does at c.

11. ( The Neighborhood Theorem) Suppose that:

(a) .

(b) for all x in the interval except possibly at c.

Then the limits $\displaystyle \lim_{x \to c} f(x)$ and $\displaystyle \lim_{x \to c} g(x)$ are either both defined or both undefined. If they are both defined, then they have the same value.