Limits: An Introduction

Calculus was originally done in an informal way, but difficulties arose. People saw the need for developing the fundamental concepts in a careful way.

Limits provide a precise way of talking about convergence and infinite processes.

Later, you'll see that two of the big ideas in calculus --- derivatives and integrals --- are defined using limits. You'll also use limits to study graphs.

Intuitively, convergence means that a variable quantity approaches a fixed number.

For instance, the following numbers seem to converge to 3:

$3.1, \quad 3.01, \quad 3.001, \quad 3.0001, \quad .$

The limit of a function as x approaches a number c is denoted

$\lim_{x \to c} f(x).$

It may be equal to a number, or it may be undefined.

In this section, I'll discuss this idea informally and intuitively, first with the aid of graphical and numerical evidence. Let's begin with a graph.

Example. The graph of a function is shown in the picture. (Each square is 1 unit by 1 unit.)

$\hbox{\epsfysize=2in \epsffile{limits-introduction-1.eps}}$

What is $\displaystyle \lim_{x \to 3} f(x)$ ?

The expression " $\displaystyle \lim_{x \to 3} f(x)$ " is read: "The limit of as x approaches (or `goes to') 3".

In words, it means the height (" ") that the graph is approaching as x gets close to 3.

To guess the value of the limit from the graph, I look at the graph for x's close to 3.

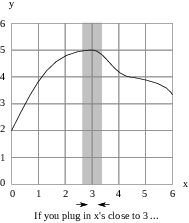
$\hbox{\epsfysize=2in \epsffile{limits-introduction-2.eps}}$

For x's close to 3, the height of the graph seems to be close to 5:

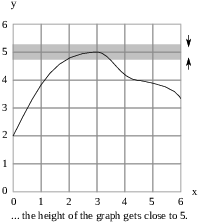
$\hbox{\epsfysize=2in \epsffile{limits-introduction-3.eps}}$

Therefore,

$\lim_{x \to 3} f(x) = 5.\quad\halmos$

By the way, the value of the function when is 5: that is,

In this case, it's the same as the value of the limit --- but in general, they can be different.

Example. The graph of a function is shown in the picture. (Each square is 1 unit by 1 unit.)

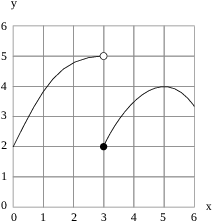
$\hbox{\epsfysize=2in \epsffile{limits-introduction-4.eps}}$

(a) What is $\displaystyle \lim_{x \to 3} f(x)$ ? (This is a trick question!)

(b) What is $\displaystyle \lim_{x \to 3^+} f(x)$ ? What is $\displaystyle \lim_{x \to 3^-} f(x)$ ? (Notice the new notation here!)

(a) I look at the graph for x's close to 3.

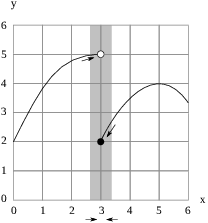
$\hbox{\epsfysize=2in \epsffile{limits-introduction-5.eps}}$

For x's close to 3, the height of the graph seems to be close to 2 ... or is it close to 5?

You can see that x's close to 3 on the right, the height of the graph is close to 2. But for x's close to 3 on the left, the height of the graph is close to 5.

When you're asked for "the value" of $\displaystyle \lim_{x \to 3} f(x)$ , you're required to give a single answer: You can't say "2 or 5". If the situation seems to require two answers, then you say:

$\lim_{x \to 3} f(x) \quad\hbox{is undefined}.\quad\halmos$

(b) Note that I was able to say that the graph was approaching definite heights from the right and left separately. You can use {\ bf right and left-hand limits} to express this.

Since for x's close to 3 on the right, the height of the graph is close to 2, the right-hand limit is 2:

$\lim_{x \to 3^+} f(x) = 2.$

(The superscript " ${}^+$ " on the "3" means that you're only considering x's to the right of 3.)

Since for x's close to 3 on the left, the height of the graph is close to 5, the left-hand limit is 5:

$\lim_{x \to 3^-} f(x) = 5.$

(The superscript " ${}^-$ " on the "3" means that you're only considering x's to the left of 3.)

It's easy to miss those superscripts, so you have to read carefully!

$\displaystyle \lim_{x \to 3} f(x)$ (with no superscripts on the "3") will just be called "the limit" (or the "two-sided limit" if I need to be extra clear).

The last example illustrates a general principle:

(a) If the left and right-hand limits are different, the (two-sided) limit is undefined.

(b) If the left and right-hand limits are the same, their common value is the value of the (two-sided) limit.

In the next example, I'll consider how you can use numerical evidence to guess the value of a limit.

Example. Use graphical and numerical evidence to guess the value of

$\lim_{x \to 2} \dfrac{x - 2}{x^2 - 4}.$

To guess the value of $\displaystyle \lim_{x \to 2} \dfrac{x - 2}{x^2 - 4}$ using numerical evidence, I set x to numbers close to 2, and look at the values of $\dfrac{x - 2}{x^2 - 4}$ :

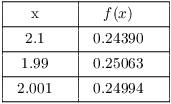
$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & x & & $f(x)$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 2.1 & & 0.24390 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 1.99 & & 0.25063 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 2.001 & & 0.24994 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }}$

I picked the values at random. (However, it's a good idea to pick some numbers smaller than 2 and some larger than 2, for reasons we'll see later.)

It seems as though the $\dfrac{x - 2}{x^2 - 4}$ -values are close to 0.25.

Notice that I don't try to plug in . In fact, $\dfrac{x - 2}{x^2 - 4}$ is not defined at : If you plug into $\dfrac{x - 2}{x^2 - 4}$ , you get

$\dfrac{2 - 2}{2^2 - 4} = \dfrac{0}{0}.$

$\dfrac{0}{0}$ is an indeterminate form. For now, you can think of this as meaning that the value of the limit can't be determined without further work.

In thinking about the limit of a function as x approaches c, you don't consider what happens when x equals c; you consider what happens when x is close to c.

To guess the value of $\displaystyle \lim_{x \to 2} \dfrac{x - 2}{x^2 - 4}$ using graphical evidence, graph the function $\dfrac{x - 2}{x^2 - 4}$ near :

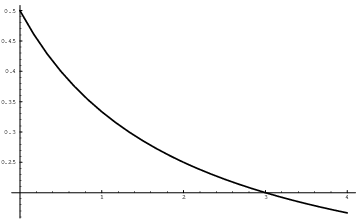
$\hbox{\epsfysize=2in \epsffile{limits-introduction-6.eps}}$

It appears that near , the height of the graph of $\dfrac{x - 2}{x^2 - 4}$ is around 0.25.

In this case, when x is close to 2, it appears that $\dfrac{x - 2}{x^2 - 4}$ is close to 0.25. In words, you would say: The limit of $\dfrac{x - 2}{x^2 - 4}$ as x approaches 2 is 0.25. In symbols, you would write

$\lim_{x\to 2} \dfrac{x - 2}{x^2 - 4} = 0.25.\quad\halmos$

As a first pass at a general definition, to say that $\displaystyle \lim_{x \to a} f(x) = L$ means that can be made arbitrarily close to L for all x's sufficiently close to a.

I'll discuss the definition and some rules for computing limits later. First, I'll show you some computations so you can get a feel for the ideas.

Example. Compute $\displaystyle \lim_{x \to 2} (4 x^3 - 5 x + 11)$ .

If I plug into , I get . Since "nothing bad happened",

$\lim_{x \to 2} (4x^3 - 5x + 11) = 33.\quad\halmos$

This is a special case of the following general rule: If is a polynomial, then

$\lim_{x\to c} p(x) = p(c).$

That is, you can compute the limit of a polynomial by "plugging the number in". When you can compute $\displaystyle \lim_{x\to c} f(x)$ by plugging in (to get ), the function f is continuous at . I'll discuss continuity in more detail later.

It would be nice if everything was this easy. In the next few examples, we'll see what to do if "something bad happens" when you plug in.

Example. Compute $\displaystyle \lim_{x \to 2} \dfrac{x - 2}{x^2 - 4}$ .

I used graphical and numerical evidence earlier to guess that the limit is $\dfrac{1}{4}$ .

If you plug 2 into $\dfrac{x - 2}{x^2 - 4}$ , you get $\dfrac{0}{0}$ . This is called an indeterminate form. This means that you can't conclude anything from the form $\dfrac{0}{0}$ : The limit might be a number, it might be infinite, or it might be undefined.

When plugging in yields an indeterminate form, you have to do more work before you can come to a conclusion. "More work" often involves algebraic simplification.

In this case, I fact , then cancel 's:

$\lim_{x \to 2} \dfrac{x - 2}{x^2 - 4} = \lim_{x \to 2} \dfrac{x - 2}{(x - 2)(x + 2)} = \lim_{x \to 2} \dfrac{1}{x + 2} = \dfrac{1}{4}.$

Why am I allowed to cancel the 's? I noted earlier that in computing $\displaystyle \lim_{x \to 2} \dfrac{x - 2}{x^2 - 4}$ I only consider x's near 2, not x equal to 2. Since $x \ne 2$ , I have $x - 2 \ne 0$ , so cancellation is legal.

I did the last step by plugging into $\dfrac{1}{x + 2}$ . This time I did not get an indeterminate form, and the rules for limits I'll discuss later tell me that $\dfrac{1}{4}$ is the answer.

Example. Compute $\displaystyle \lim_{x \to 1} \dfrac{x^3 - 1}{x - 1}$ .

If you plug into $\dfrac{x^3 - 1}{x - 1}$ , you get $\dfrac{0}{0}$ . This means you have more work to do.

From basic algebra, we have the factoring rule

$\lim_{x \to 1} \dfrac{x^3 - 1}{x - 1} = \lim_{x \to 1} \dfrac{(x - 1)(x^2 + x + 1)}{x - 1} = \lim_{x \to 1} (x^2 + x + 1) = 3.\quad\halmos$

Example. Compute 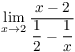$\displaystyle \lim_{x \to 2} \dfrac{x - 2}{\dfrac{1}{2} - \dfrac{1}{x}}$ .

Plugging in gives $\dfrac{0}{0}$ . I have more work to do. There are several approaches you can take. One is to multiply the top and bottom of the big fraction to clear the denominators of the little fractions on the bottom:

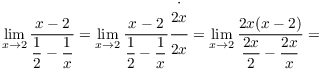
$\lim_{x \to 2} \dfrac{x - 2}{\dfrac{1}{2} - \dfrac{1}{x}} = \lim_{x \to 2} \dfrac{x - 2}{\dfrac{1}{2} - \dfrac{1}{x}} \dot \dfrac{\vphantom{\dfrac{x}{x}} 2 x}{\vphantom{\dfrac{x}{x}} 2 x} = \lim_{x \to 2} \dfrac{2 x (x - 2)}{\dfrac{2 x}{2} - \dfrac{2 x}{x}} =$

$\lim_{x \to 2} \dfrac{2 x (x - 2)}{x - 2} = \lim_{x \to 2} 2 x = 4.$

Another approach is to add the fractions on the top and simplify:

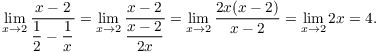
$\lim_{x \to 2} \dfrac{x - 2}{\dfrac{1}{2} - \dfrac{1}{x}} = \lim_{x \to 2} \dfrac{x - 2}{\dfrac{x - 2}{2x}} = \lim_{x \to 2} \dfrac{2x(x - 2)}{x - 2} = \lim_{x \to 2} 2x = 4.$

I got the last equality by plugging 2 into and using the rule for polynomials. Notice a common thread in the last few problems. If plugging into produces a $\dfrac{0}{0}$ form, something must be producing the 0's. Often it is a common factor, which can be cancelled from the top and bottom when you've identified it.

Example. Compute $\displaystyle \lim_{x \to 3} \dfrac{x - 3}{\sqrt{x} - \sqrt{3}}$ .

If you plug into $\dfrac{x - 3}{\sqrt{x} - \sqrt{3}}$ , you get $\dfrac{0}{0}$ . This means you have some work to do.

Once again, there are several approaches you could take. One is to multiply the top and bottom by the conjugate of $\sqrt{x} - \sqrt{3}$ :

$\lim_{x \to 3} \dfrac{x - 3}{\sqrt{x} - \sqrt{3}} = \lim_{x \to 3} \dfrac{x - 3}{\sqrt{x} - \sqrt{3}} \cdot \dfrac{\sqrt{x} + \sqrt{3}}{\sqrt{x} + \sqrt{3}} = \lim_{x \to 3} \dfrac{(x - 3)(\sqrt{x} + \sqrt{3})}{(\sqrt{x} - \sqrt{3})(\sqrt{x} + \sqrt{3})} =$

$\lim_{x \to 3} \dfrac{(x - 3)(\sqrt{x} + \sqrt{3})}{x - 3} = \lim_{x \to 3} (\sqrt{x} + \sqrt{3}) = 2 \sqrt{3}.$

Another approach (which may be harder to see) is to factor :

$x - 3 = (\sqrt{x} - \sqrt{3})(\sqrt{x} + \sqrt{3}).$

Then

$\lim_{x \to 3} \dfrac{x - 3}{\sqrt{x} - \sqrt{3}} = \lim_{x \to 3} \dfrac{(\sqrt{x} - \sqrt{3})(\sqrt{x} + \sqrt{3})}{\sqrt{x} - \sqrt{3}} = \lim_{x \to 3} (\sqrt{x} + \sqrt{3}) = 2 \sqrt{3}.$

The answer seems to be confirmed by the graph; $2 \sqrt{3} \approx 3.5$ , and here is the graph:

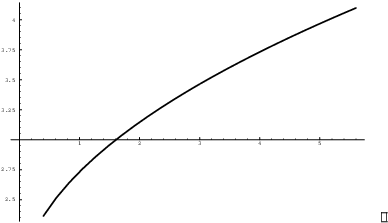
$\hbox{\epsfysize=2in \epsffile{limits-introduction-7.eps}}\quad\halmos$

Example. Compute $\displaystyle \lim_{x \to 1} \dfrac{x^2 - 2x - 3}{x - 1}$ .

Plugging in gives $\dfrac{-4}{0}$ . This is not the same as $\dfrac{0}{0}$ : In this case, the limit is undefined.

The graph shows a vertical asymptote at :

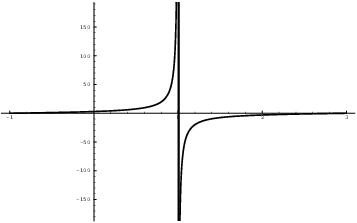
$\hbox{\epsfysize=2in \epsffile{limits-introduction-8.eps}}$

If I plug in values of x near 1, I get a wide range of outputs:

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0.9 & & 0.999 & & 1.0003 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $f(x)$ & & 39.9 & & 4000 & & -13333.3 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

These empirical results seem to confirm that the limit is undefined.

The general rule is: If you plug in and get $\dfrac{\hbox{nonzero number}}{0}$ , the limit is undefined.

Contact information

Bruce Ikenaga's Home Page