Log and Exponential Derivatives

Here are the formulas for the derivatives of $\ln x$ and $e^x$ :

$$\der {} x \ln x = \dfrac{1}{x} \quad\hbox{and}\quad \der {} x e^x = e^x.$$

I'll derive them at the end. First, I'll give some examples to show how they're used.

Example. Compute $\displaystyle \der {} x x^{10} \ln x$ .

Using the Product Rule, I get

$$\der {} x x^{10} \ln x = x^{10} \cdot \dfrac{1}{x} + (\ln x)(10 x^9) = x^9 + 10 x^9 \ln x.\quad\halmos$$

Note: Don't write "$\ln x 10 x^9$ " for the second term, since that means "$\ln (x \cdot 10 x^9)$ ". Either put the "$10 x^9$ " on the left side of the log, or write "$(\ln x)(10 x^9)$ ".

Example. Find the equation of the tangent line to $f(x) = x^2 \ln x$ at $x = e$ .

Since $f(e) = e^2 \ln 3 = e^2$ , the point of tangency is $(e, e^2)$ .

Using the Product Rule, I find that the derivative is

$$f'(x) = x^2 \cdot \dfrac{1}{x} + (\ln x)(2 x) = x + 2 x \ln x.$$

The slope of the tangent at $x = e$ is

$$f'(e) = e + 2 e \ln e = e + 2 e \cdot 1 = 3 e.$$

The equation of the tangent line is

$$y - e^2 = 3 e (x - e), \quad\hbox{or}\quad y = 3 e x -2 e^2.\quad\halmos$$

Example. For what values of x does $y = x \ln x$ have a horizontal tangent?

Using the Product Rule, I find that

$$y' = x \cdot \dfrac{1}{x} + (\ln x)(1) = 1 + \ln x.$$

The tangent line is horizontal when the derivative is equal to 0. Set $y' = 0$ and solve for x:

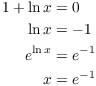
$$\eqalign{ 1 + \ln x & = 0 \cr \ln x & = -1 \cr e^{\ln x} & = e^{-1} \cr x & = e^{-1} \cr}$$

(To go from the third equation to the fourth, I used the fact that $e^{\ln (\hbox{\eightrm junk})} = (\hbox{junk})$ .) There is a horizontal tangent when $x = e^{-1}$ .

Here are several examples using the Chain Rule. Do you see the pattern?

$$\der {} x \ln (x^3 + 1) = \dfrac{3 x^2}{x^3 + 1}.$$

$$\der {} x \ln \sin x = \dfrac{\cos x}{\sin x}.$$

$$\der {} x \ln (83 x + 17) = \dfrac{83}{83 x + 17}.$$

$$\der {} x \ln (e^x + 13 x) = \dfrac{e^x + 13}{e^x + 13 x}.$$

In all of these cases,

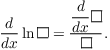
$$\der {} x \ln \square = \dfrac{\der {} x \square}{\square}.$$

I'll often use this rule in differentiating logs.

The technique used in the next two examples is called logarithmic differentiation. It gives a useful way of differentiating expressions of the form $P(x)^{Q(x)}$ , where both P and Q are functions of x.

Example. ( Logarithmic differentiation) Compute $\der {} x x^x$ .

You can't use the Power Rule, because the power is x, not a number.

To do this, first, set $y = x^x$ . Take logs:

$$\ln y = \ln x^x = x \ln x.$$

Notice that I used the log rule

$$\ln A^B = B \ln A.$$

Now differentiate both sides of $\ln y = x \ln x$ . You need the Chain Rule on the left (or the rule from the last example), and the Product Rule on the right:

$$\eqalign{ \dfrac{y'}{y} & = (x)\left(\dfrac{1}{x}\right) + (\ln x)(1) \cr \noalign{\vskip2pt} y' & = y (1 + \ln x) \cr y' & = x^x (1 + \ln x) \quad\halmos \cr}$$

Note: It's also possible to do this by writing

$$x^x = e^{\ln x^x} = e^{x \ln x}.$$

You can differentiate $e^{x \ln x}$ using the Chain Rule.

Example. ( Logarithmic differentiation) Compute $\der {} x (x^2 + 9)^{\sin x}$ .

$$\eqalign{ y & = (x^2 + 9)^{\sin x} \cr \ln y & = \ln (x^2 + 9)^{\sin x} \cr \ln y & = (\sin x) \ln (x^2 + 9) \cr \noalign{\vskip2pt} \dfrac{y'}{y} & = (\sin x)\left(\dfrac{2 x}{x^2 + 9}\right) + [\ln (x^2 + 9)](\cos x) \cr \noalign{\vskip2pt} y' & = y \left((\sin x)\left(\dfrac{2 x}{x^2 + 9}\right) + [\ln (x^2 + 9)](\cos x)\right) \cr \noalign{\vskip2pt} y' & = (x^2 + 9)^{\sin x} \left((\sin x)\left(\dfrac{2 x}{x^2 + 9}\right) + [\ln (x^2 + 9)](\cos x)\right) \quad\halmos \cr}$$

Now here are some examples using the differentiation rule for $e^x$ .

Example. Compute $\displaystyle \der {} x \dfrac{3 e^x + 1}{4 x^{11} + 3 x + 1}$ .

Using the Quotient Rule, I get

$$\der {} x \dfrac{3 e^x + 1}{4 x^{11} + 3 x + 1} = \dfrac{(4 x^{11} + 3 x + 1)(3 e^x) - (3 e^x + 1)(44 x^{10} + 3)}{(4 x^{11} + 3 x + 1)^2}.\quad\halmos$$

Example. Find the value(s) of x for which $y = x e^{8 x}$ has a horizontal tangent.

Using the Product Rule, I have

$$y' = (x)(8 e^{8 x}) + e^{8 x} = 8 x e^{8 x} + e^{8 x}.$$

Since I'm looking for horizontal tangents, I set $y' = 0$ and solve for x:

$$\eqalign{ 8 x e^{8 x} + e^{8 x} & = 0 \cr (8 x + 1) e^{8 x} & = 0 \cr}$$

Since $e^{8 x}$ can't ever equal 0, I may divide it out. This gives $8 x + 1 = 0$ , or $x = -\dfrac{1}{8}$ .

Here are several examples using the Chain Rule. Do you see the pattern?

$$\der {} x e^{(x^3 + 4)} = 3 x^2 e^{(x^3 + 4)}.$$

$$\der {} x e^{(13 x + 5)} = 13 e^{(13 x + 5)}.$$

$$\der {} x e^{\cot x} = -(\csc x)^2 e^{\cot x}.$$

$$\der {} x e^{1/x} = \left(-\dfrac{1}{x^2}\right) e^{1/x}.$$

In all of these cases,

$$\der {} x e^{\square} = \left(\der {} x \square\right) e^{\square}.$$

I'll often use this formula in differentiating exponentials.

Remark. Sometimes you may have expressions like

$$e^{(3 x^4 + 2 x^3 - 17 x + 9)}.$$

The power is so large that it's inconvenient to write in the usual "superscript" form. For one thing, the smaller font can make it hard to read. In situations like this, you can use exponential notation:

$$\exp A = e^A.$$

Thus, the preceding expression can be written as

$$\exp (3 x^4 + 2 x^3 - 17 x + 9).\quad\halmos$$

You can use the formula for the derivative of $\ln x$ to derive the formula for differentiating logs to other bases.

Suppose that $a > 0$ . The conversion formula for logs says that

$$\log_a x = \dfrac{\ln x}{\ln a}.$$

Therefore, since $\dfrac{1}{\ln a}$ is constant,

$$\der {} x \log_a x = \der {} x \dfrac{\ln x}{\ln a} = \dfrac{1}{\ln a} \der {} x \ln x = \dfrac{1}{\ln a} \cdot \dfrac{1}{x} = \dfrac{1}{x \ln a}.$$

In other words, the formula for differentiating $\log_a x$ is

$$\der {} x \log_a x = \dfrac{1}{x \ln a}.$$

Example. Compute:

(a) $\displaystyle \der {} x \log_{17} x$ .

(b) $\displaystyle \der {} x \log_3 (x^4 + 5 x + 2)$ .

(c) $\displaystyle \der {} x x^2 \log_{10} x$ .

(a)

$$\der {} x \log_{17} x = \dfrac{1}{x \ln 17}.\quad\halmos$$

(b)

$$\der {} x \log_3 (x^4 + 5 x + 2) = \dfrac{4 x^3 + 5}{(x^4 + 5 x + 2) \ln 3}.\quad\halmos$$

(c)

$$\der {} x x^2 \log_{10} x = (x^2) \left(\dfrac{1}{x \ln 10}\right) + (\log_{10} x)(2 x).\quad\halmos$$

What about exponentials to other bases?

Let $y = a^x$ . Then

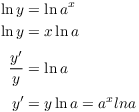
$$\eqalign{ \ln y & = \ln a^x \cr \ln y & = x \ln a \cr \noalign{\vskip2pt} \dfrac{y'}{y} & = \ln a \cr \noalign{\vskip2pt} y' & = y \ln a = a^x ln a \cr}$$

I used the Chain Rule to differentiate $\ln y$ . The rule is:

$$\der {} x a^x = a^x \ln a.$$

Notice that when $a = e$ , the formula becomes

$$\der {} x e^x = e^x \ln e = e^x \cdot 1 = e^x.$$

This agrees with the differentiation formula for $e^x$ .

Example. Compute:

(a) $\displaystyle \der {} x \left(\dfrac{355}{113}\right)^x$ .

(b) $\displaystyle 7^x \log_8 x$ .

(c) $\displaystyle \dfrac{2^x + 3^x}{4^x + 5^x}$ .

(a)

$$\der {} x \left(\dfrac{355}{113}\right)^x = \left(\dfrac{355}{113}\right)^x \ln \dfrac{355}{113}.\quad\halmos$$

(b)

$$\der {} x 7^x \log_8 x = (7^x)\left(\dfrac{1}{x\ln 8}\right) + (\log_8 x)(7^x \ln 7).\quad\halmos$$

(c)

$$\der {} x \dfrac{2^x + 3^x}{4^x + 5^x} = \dfrac{(4^x + 5^x)(2^x\ln 2 + 3^x\ln 3) - (2^x + 3^x)(4^x\ln 4 + 5^x\ln 5)}{(4^x + 5^x)^2}.\quad\halmos$$

Now I'll show where the derivative formulas for $\ln x$ and $e^x$ come from. I have to begin with a precise definition.

If $x \ge 1$ , then $\ln x$ , the natural log of x, is defined to be the area under the graph of $y = \dfrac{1}{t}$ from 1 to x:

$$\hbox{\epsfysize=1.5in \epsffile{log-and-exponential-derivatives1.eps}}$$

Note that since a segment has zero area, $\ln 1 = 0$ .

If $x < 1$ , then $\ln x$ is the negative of the area under the graph from 1 to x.

This may not be the definition you're familiar with from earlier courses, but it turns out to give the same thing. The advantage of this definition is that it's good for doing calculus.

What is $\der {} x \ln x$ ? The definition of the derivative says if $f(x) = \ln x$ , then

$$f'(x) = \lim_{h \to 0} \dfrac{\ln(x + h) - \ln x}{h}.$$

Now

$$\ln (x + h) \quad\hbox{is the area under the curve from}\quad 1 \quad\hbox{to}\quad x + h,$$

$$\ln x \quad\hbox{is the area under the curve from}\quad 1 \quad\hbox{to}\quad x.$$

So by subtraction, the top of the fraction $\ln (x + h) - \ln x$ is the shaded area in this picture:

$$\hbox{\epsfysize=1.75in \epsffile{log-and-exponential-derivatives2.eps}}$$

Build two rectangles, one below the curve and one above the curve:

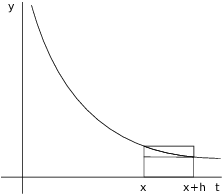
$$\hbox{\epsfysize=1.75in \epsffile{log-and-exponential-derivatives3.eps}}$$

Obviously,

$$(\hbox{little rectangle area}) < \ln (x + h) - \ln x < (\hbox{big rectangle area}). \eqno{\rm (*)}$$

Both rectangles have base $(x + h) - x = h$ .

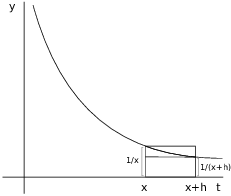
$$\hbox{\epsfysize=1.75in \epsffile{log-and-exponential-derivatives4.eps}}$$

The height of the big rectangle is $\dfrac{1}{x}$ (that is, x plugged into the curve equation $y = \dfrac{1}{t}$ ).

The height of the little rectangle is $\dfrac{1}{x + h}$ .

Therefore,

$$(\hbox{big rectangle area}) = h \cdot \dfrac{1}{x} \quad\hbox{and}\quad (\hbox{little rectangle area}) = h \cdot \dfrac{1}{x + h}.$$

Plugging these into (*) above and dividing by h, I get

$$h \cdot \dfrac{1}{x + h} < \ln (x + h) - \ln x < h \cdot \dfrac{1}{x},$$

$$\dfrac{1}{x + h} < \dfrac{\ln (x + h) - \ln x}{h} < \dfrac{1}{x}.$$

Now take the limit as $h \to 0$ .

On the left side, $\dfrac{1}{x + h} \to \dfrac{1}{x}$ .

On the right side, $\dfrac{1}{x} \to \dfrac{1}{x}$ .

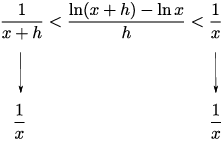
$$\hbox{\epsfysize=1.25in \epsffile{log-and-exponential-derivatives5.eps}}$$

By the Squeezing Theorem,

$$\lim_{h \to 0} \dfrac{\ln (x + h) - \ln x}{h} = \dfrac{1}{x}.$$

(Actually, I've done this for $h > 0$ , so this is the right-hand limit, but a similar argument works for the left-hand limit.)

I've shown that

$$\der {} x \ln x = \dfrac{1}{x}.$$

What about $e^x$ ? In order to derive its derivative, I need a reasonably precise definition of this function.

Look at the picture I used to define $\ln x$ :

$$\hbox{\epsfysize=1.5in \epsffile{log-and-exponential-derivatives1.eps}}$$

As x increases, the area increases. This means that $\ln x$ is one-to-one: If $a \ne b$ , then $\ln a \ne \ln b$ .

This in turn means that $\ln x$ has an inverse function. I'll denote the inverse function by $e^x$ .

Since $f^{-1}(x) = e^x$ for $f(x) = \ln x$ , I can use the formula for the derivative of an inverse function to get the derivative formula for $e^x$ .

The formula for the derivative of an inverse function says

$$(f^{-1})'(x) = \dfrac{1}{f'(f^{-1}(x))}.$$

Since $f(x) = \ln x$ , I have $f'(x) = \dfrac{1}{x}$ . So

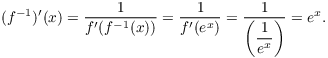
$$(f^{-1})'(x) = \dfrac{1}{f'(f^{-1}(x))} = \dfrac{1}{f'(e^x)} = \dfrac{1}{\left(\dfrac{1}{e^x}\right)} = e^x.$$

I've shown that

$$\der {} x e^x = e^x.$$

You may still be uncomfortable by the way I defined $\ln x$ and $e^x$ , since they may not correspond to the way they were defined for you in (say) precalculus courses. In order to justify these definitions better, later on I'll reinterpret the area definition for $\ln x$ as a definite integral. Then I'll be able to show that $\ln x$ , by this definition, has all the properties you'd expect a log function to have, such as

$$\ln A B = \ln A + \ln B \quad\hbox{or}\quad \ln A^B = B \ln A.$$

I'll also be able to justify the corresponding properties for $e^x$ , and this will show that these new definitions "agree with" the ones you may have seen earlier.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga