Max-min Word Problems

In this section, we'll use our results on maxima and minima for functions to do word problems which involve finding the largest or smallest value of lengths, areas, volumes, costs, and so on. The hardest part of doing these problems is setting up the appropriate equations; the calculus part is relatively simple.

Some of these problems involve finding an absolute max or min on a closed interval. We know that to do this, we find the critical points on the interval, then test the endpoints and the critical points in the original function.

In some situations, the quantity we're trying to maximize or minimize varies over a non-closed interval. In those cases, the following theorem is often useful.

Theorem. Suppose a function f has its second derivative $f''$ defined on an interval $a < x < b$ . Suppose that $f'(c) = 0$ , and that c is the only critical point on the interval $a < x < b$ .

(a) If c is a local max, then it is an absolute max.

(b) If c is a local min, then it is an absolute min.

The key in applying the theorem is that there is only one critical point.

Example. A rectangular pen consists of two identical sections separated by a fence. 120 feet of fence is used for the outside of the pen and the dividing fence. What dimensions for each section produce the pen of largest area?

Let each section be x feet in width and y feet in height.

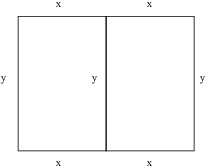
$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-1.eps}}$$

The total area is

$$A = 2 x y.$$

Since 120 feet of fence are available,

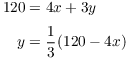
$$\eqalign{ 120 & = 4 x + 3 y \cr \noalign{\vskip2pt} y & = \dfrac{1}{3} (120 - 4 x) \cr}$$

Plug this into $A = 2 x y$ :

$$A = 2 x \cdot \dfrac{1}{3} (120 - 4 x) = \dfrac{2}{3} (120 x - 4 x^2).$$

The endpoints are given by the extreme cases $x = 0$ and $y = 0$ ; note that $y = 0$ gives

$$120 = 4 x, \quad\hbox{or}\quad x = 30.$$

Differentiate:

$$A' = \dfrac{2}{3} (120 - 8 x).$$

Set $A' = 0$ and solve for x:

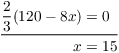
$$\eqalign{ \dfrac{2}{3} (120 - 8 x) & = 0 \cr \noalign{\vskip2pt \hrule \vskip2pt} x & = 15 \cr}$$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 15 & & 30 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & A & & 0 & & 600 & & 0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The maximum occurs when $x = 15$ . In this case,

$$y = \dfrac{1}{3} \left(120 - 4 \cdot 15\right) = 20.\quad\halmos$$

Example. A rectangular sheet of cardboard is 15 wide and 24 inches high. Squares with sides of length x are cut out of each corner. The four resulting tabs are folded up to make a rectangular box (with no top). Find the value of x which gives the box of largest volume.

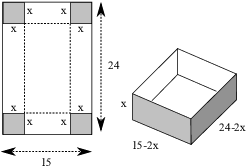
$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-2.eps}}$$

The base of the box is $15 - 2 x$ by $24 - 2 x$ , and the height is x. Hence, the volume is

$$V = x(15 - 2 x)(24 - 2 x) = 4 x^3 - 78 x^2 + 360 x.$$

The endpoints are $x = 0$ (cut no squares out) and $x = \dfrac{15}{2}$ (cut halfway from the bottom to the top). Obviously, these endpoints give volume 0, but it means that V is defined on a closed interval. So I just need to test the critical points on the interval and find the one that gives a max.

Differentiate:

$$V' = 12 x^2 - 156 x + 360 = 12 (x^2 - 13 x + 30) = 12 (x - 3)(x - 10).$$

The roots are $x = 10$ and $x = 3$ .

Now $x = 10$ is greater than $\dfrac{15}{2}$ , so it's outside the interval. So I only need to consider the other root $x = 3$ .

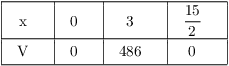
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 3 & & $\dfrac{15}{2}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & V & & 0 & & 486 & & 0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus, $x = 3$ maximimizes the volume.

Example. A rectangular poster is printed on a piece of cardboard with area 1200 square inches. The printed region is a rectangular region centered on the cardboard. There are unprinted (blank) margins of width 3 inches on the left and right of the printed region, and width 4 inches on the top and bottom of the printed region.

What dimensions for the printed region maximize its area?

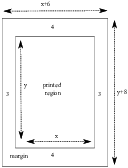
$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-3.eps}}$$

Suppose the printed area is x by y. Its area is

$$A = x y.$$

Since there are margins of width 3 on the left and right, and margins of width 4 on top and bottom, the area of the cardboard is

$$(x + 6)(y + 8) = 1200.$$

Solving for y yields

$$y = \dfrac{1200}{x + 6} - 8.$$

Plug this into the expression for A to obtain

$$A = x \left(\dfrac{1200}{x + 6} - 8\right) = \dfrac{1200 x}{x + 6} - 8 x.$$

The extreme cases are $x = 0$ and $y = 0$ . If $y = 0$ , then

$$\eqalign{ (x + 6)(8) & = 1200 \cr \noalign{\vskip2pt} x & = 144 \cr}$$

So the endpoints are $x = 0$ and $x = 144$ . (These make the area of the printed region 0, so they obviously don't give the maximum!)

Compute the derivative:

$$A' = \dfrac{(x + 6)(1) - (1200 x)(1)}{(x + 6)^2} - 8 = \dfrac{7200}{(x + 6)^2} - 8.$$

Find the critical points:

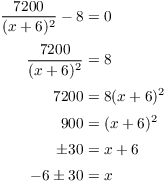
$$\eqalign{ \dfrac{7200}{(x + 6)^2} - 8 & = 0 \cr \noalign{\vskip2pt} \dfrac{7200}{(x + 6)^2} & = 8 \cr \noalign{\vskip2pt} 7200 & = 8 (x + 6)^2 \cr \noalign{\vskip2pt} 900 & = (x + 6)^2 \cr \noalign{\vskip2pt} \pm 30 & = x + 6 \cr \noalign{\vskip2pt} -6 \pm 30 & = x \cr}$$

Since x is a length, it can't be negative, so take the plus sign. This gives

$$x = 30 - 6 = 24.$$

Plug this into $y = \dfrac{1200}{x + 6} - 8$ to get $y = 32$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 24 & & 144 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & A & & 0 & & 768 & & 0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

This shows that $x = 24$ and $y = 32$ maximize the area of the printed region.

Example. Find the point on the line $8 y - x + 3 = 0$ which is closest to the point $(1, 6)$ .

The distance from $(x, y)$ to $(1, 6)$ is

$$d = \sqrt{(x - 1)^2 + (y - 6)^2}.$$

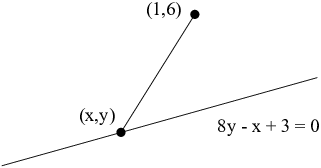
$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-4.eps}}$$

I want the point $(x, y)$ for which the distance is smallest.

Since smaller numbers give smaller squares and vice versa, I can find where the square of the distance is smallest:

$$s = (x - 1)^2 + (y - 6)^2.$$

This allows me to remove the square root, and will make differentiation easier.

The line is $8y - x + 3 = 0$ . Solving for x gives $x = 8 y + 3$ . Plug this into the equation for s:

$$S = [(8 y + 3) - 1]^2 + (y - 6)^2 = (8 y + 2)^2 + (y - 6)^2.$$

There are no restrictions on x, so I'll use the Second Derivative Test. Differentiate (noting that the variable is y):

$$s' = 2(8 y + 2)(8) + 2(y - 6) = 128 y + 32 + 2 y - 12 = 130 y + 20,$$

$$s'' = 130.$$

Set $s' = 0$ to find the critical points:

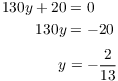
$$\eqalign{ 130 y + 20 & = 0 \cr 130 y & = -20 \cr \noalign{\vskip2pt} y & = -\dfrac{2}{13} \cr}$$

This gives

$$x = 8 \cdot \left(-\dfrac{2}{13}\right) + 3 = \dfrac{23}{13}.$$

Now $s''\left(-\dfrac{2}{13}\right) = 130 > 0$ , so $y = -\dfrac{2}{13}$ is a local min. Since it's the only critical point, it's an absolute min.

Example. The volume of a circular cylinder (with a top and a bottom) is $2000 \pi$ . What values for the radius r and the height h give the smallest total surface area (the area of the side plus the area of the top plus the area of the bottom)?

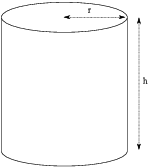
$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-5.eps}}$$

The area of the side is $2 \pi r h$ , the area of the top is $\pi r^2$ , and the area of the bottom is $\pi r^2$ .

The total surface area is

$$A = 2 \pi r h + 2 \pi r^2.$$

The volume is

$$2000 \pi = \pi r^2 h, \quad\hbox{so}\quad 2000 = r^2 h.$$

Solving for h gives $h = \dfrac{2000}{r^2}$ . Plug this into A:

$$A = 2 \pi r \cdot \dfrac{2000}{r^2} + 2 \pi r^2 = \dfrac{4000 \pi}{r} + 2 \pi r^2.$$

The only restriction on r is $r > 0$ . Hence, r is not restricted to a closedinterval $a \le r \le b$ . Therefore, I'll use the Second Derivative Test.

Compute $A'$ and $A''$ :

$$A' = -\dfrac{4000 \pi}{r^2} + 4 \pi r,$$

$$A'' = \dfrac{8000 \pi}{r^3} + 4 \pi.$$

Set $A' = 0$ and solve for r:

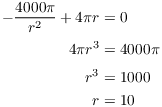
$$\eqalign{ -\dfrac{4000 \pi}{r^2} + 4 \pi r & = 0 \cr \noalign{\vskip2pt} 4 \pi r^3 & = 4000 \pi \cr \noalign{\vskip2pt} r^3 & = 1000 \cr r & = 10 \cr}$$

This gives $h = \dfrac{2000}{100} = 20$ .

Now

$$A''(k) = \dfrac{8000 \pi}{1000} + 4 \pi = 12 \pi > 0.$$

Hence, $r = 10$ is a local min. Since it's the only critical point, it's an absolute min.

Example. A cylindrical can with a top and a bottom is made with $1536 \pi$ square inches of sheet metal, with no waste. What dimensions for the radius r and the height h give the can of largest volume?

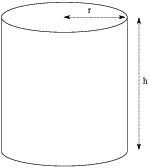
$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-6.eps}}$$

$$V = \pi r^2 h.$$

The area of the top is $\pi r^2$ , the area of the bottom is $\pi r^2$ , and the area of the side is $2 \pi r h$ . So the total area is

$$1536 \pi = 2 \pi r^2 + 2 \pi r h.$$

Solve the equation for h:

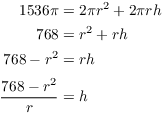
$$\eqalign{ 1536 \pi & = 2 \pi r^2 + 2 \pi r h \cr 768 & = r^2 + r h \cr 768 - r^2 & = r h \cr \noalign{\vskip2pt} \dfrac{768 - r^2}{r} & = h \cr}$$

Substitute in V:

$$V = \pi r^2 \cdot \dfrac{768 - r^2}{r} = \pi r(768 - r^2) = \pi (768 r - r^3).$$

$r = 0$ is ruled out, because it would cause division by 0 in the equation for h. There is no other restriction on r, except that it should be positive. Since V is not restricted to a closed interval $[a, b]$ , I'll use the Second Derivative Test.

Compute the derivatives:

$$V' = \pi (768 - 3 r^2),$$

$$V'' = \pi (-6 r) = -6 \pi r.$$

Find the critical points:

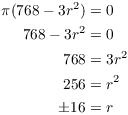
$$\eqalign{ \pi (768 - 3 r^2) & = 0 \cr 768 - 3 r^2 & = 0 \cr 768 & = 3 r^2 \cr 256 & = r^2 \cr \pm 16 & = r \cr}$$

Since r can't be negative (as it's the radius of a cylinder), I get $r = 16$ . Then

$$h = \dfrac{768 - 256}{16} = 32.$$

The second derivative is

$$V''(k) = -6 \pi \cdot 16 = -96 \pi < 0.$$

Thus, $r = 16$ is a local max. Since it's the only critical point, it's an absolute max.

Example. Find the positive number for which the sum of 5 times the number and 320 times its reciprocal is smallest.

Let x be the number. The sum of 5 times the number and 320 times its reciprocal is

$$S = 5 x + 320 \cdot \dfrac{1}{x} = 5 x + \dfrac{320}{x}.$$

The only restriction on x is $x > 0$ . Since x is not restricted to a closed interval $[a, b]$ , I'll use the Second Derivative Test.

Differentiate:

$$S' = 5 - \dfrac{320}{x^2},$$

$$S'' = \dfrac{640}{x^3}.$$

Find the critical points by setting $S' = 0$ :

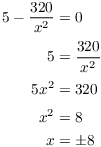
$$\eqalign{ 5 - \dfrac{320}{x^2} & = 0 \cr \noalign{\vskip2pt} 5 & = \dfrac{320}{x^2} \cr \noalign{\vskip2pt} 5 x^2 & = 320 \cr \noalign{\vskip2pt} x^2 & = 8 \cr x & = \pm 8 \cr}$$

Since $x > 0$ , I get $x = 8$ . Plug this into the Second Derivative:

$$S'' = \dfrac{640}{8} = 10 > 0.$$

Hence, $x = 8$ is a local min. Since it's the only critical point, it's an absolute min.

Example. A rectangular box with a square bottom and no top is made with 1200 square inches of cardboard. What values of the length x of a side of the bottom and the height y give the box with the largest volume?

$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-7.eps}}$$

The volume is

$$V = x^2 y.$$

The area of the 4 sides is $4 x y$ , and the area of the bottom is $x^2$ . So

$$1200 = 4 x y + x^2.$$

Solving for y gives

$$y = \dfrac{1200 - x^2}{4 x}.$$

Plug this into V and simplify:

$$V = x^2 \cdot \dfrac{1200 - x^2}{4 x} = \dfrac{1}{4} x (1200 - x^2) = \dfrac{1}{4} (1200 x - x^3).$$

Note that $x \ne 0$ , since $x = 0$ plugged into $1200 = 4 x y + x^2$ gives $1200 = 0$ a contradiction. So the only restriction on x is that $x > 0$ .

Since x is not restricted to a closed interval $[a, b]$ , I'll use the Second Derivative Test.

Compute the derivatives:

$$V' = \dfrac{1}{4} (1200 - 3 x^2).$$

$$V'' = \dfrac{1}{4} \cdot (-6 x) = -\dfrac{3}{2} x.$$

Find the critical points:

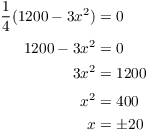
$$\eqalign{ \dfrac{1}{4} (1200 - 3 x^2) & = 0 \cr \noalign{\vskip2pt} 1200 - 3 x^2 & = 0 \cr 3 x^2 & = 1200 \cr \noalign{\vskip2pt} x^2 & = 400 \cr x & = \pm 20 \cr}$$

Since x is a length, it must be positive, so $x = 20$ . This gives

$$y = \dfrac{1200 - 400}{80} = 10.$$

Plug $x = k$ into the Second Derivative:

$$V''(k) = -\dfrac{3}{2} \cdot 20 = -30 < 0.$$

$x = 20$ is a local max, but it's the only critical point, so it's an absolute max.

Example. A rectangular box with a square bottom and no top has a volume of 2048 cubic inches. What values of the length x of a side of the bottom and the height y give the box with the smallest total surface area (the area of the bottom plus the area of the sides)?

$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-8.eps}}$$

The area of the 4 sides is $4 x y$ , and the area of the bottom is $x^2$ . So the total area is

$$A = 4 x y + x^2.$$

The volume is

$$2048 = x^2 y.$$

Solving for y gives

$$y = \dfrac{2048}{x^2}.$$

Plug this into A and simplify:

$$A = 4 x \cdot \dfrac{2048}{x^2} + x^2 = \dfrac{8192}{x} + x^2.$$

Note that $x \ne 0$ , since $x = 0$ plugged into $2048 = x^2 y$ gives $2048 = 0$ , a contradiction. So the only restriction on x is that $x > 0$ .

Since x is not restricted to a closed interval $[a, b]$ , I'll use the Second Derivative Test.

Compute the derivatives:

$$A' = -\dfrac{8192}{x^2} + 2 x,$$

$$A'' = \dfrac{16384}{x^3} + 2.$$

Find the critical points:

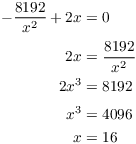
$$\eqalign{ -\dfrac{8192}{x^2} + 2 x & = 0 \cr \noalign{\vskip2pt} 2 x & = \dfrac{8192}{x^2} \cr 2 x^3 & = 8192 \cr \noalign{\vskip2pt} x^3 & = 4096 \cr x & = 16 \cr}$$

$x = 16$ gives

$$y = \dfrac{2048}{256} = 8.$$

Plug $x = 16$ into the Second Derivative:

$$A''(16) = \dfrac{16384}{4096} + 2 = 6 > 0.$$

$x = 16$ is a local min, but it's the only critical point, so it's an absolute min.

Example. A rectangular box is made with cardboard. It has no top, and consists of two identical partitions separated by a common wall. Each partition has a square bottom which is x inches by x inches, and the height of the box is y inches. If the volume of the whole box is 10584 cubic inches, what values for x and y minimize the total amount of cardboard used (for the bottom, the four sides, and the divider that separates the partitions)?

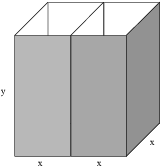
$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-9.eps}}$$

The area of the bottom is $2 x^2$ .

The front and back are each $2 x$ by y, so they have a total area of $2 \cdot 2 x y = 4 x y$ .

The right side, left side, and the middle partition are each x by y, so they have a total area of $3 x y$ .

Therefore, the total area (the total amount of cardboard used) is

$$A = 2 x^2 + 4 x y + 3 x y = 2 x^2 + 7 x y.$$

The total volume is

$$10584 = 2 x^2 y.$$

Solving this equation for y gives

$$y = \dfrac{5292}{x^2}.$$

Plug this into A and simplify:

$$A = 2 x^2 + 7 x \cdot \dfrac{5292}{x^2} = 2 x^2 + \dfrac{37044}{x}.$$

The extreme case $x = 0$ is ruled out, because it causes division by 0 in the equation for A. Thus, x is not restricted to a closed interval $[a, b]$ , and I'll use the Second Derivative Test.

Differentiate:

$$A' = 4 x - \dfrac{37044}{x^2},$$

$$A'' = 4 + \dfrac{74088}{x^3}.$$

Find the critical points by setting $A' = 0$ and solving for x:

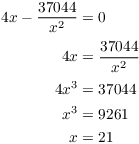
$$\eqalign{ 4 x - \dfrac{37044}{x^2} & = 0 \cr \noalign{\vskip2pt} 4 x & = \dfrac{37044}{x^2} \cr \noalign{\vskip2pt} 4 x^3 & = 37044 \cr x^3 & = 9261 \cr x & = 21 \cr}$$

This gives

$$y = \dfrac{5292}{441} = 12.$$

Do the Second Derivative Test:

$$V''(21) = 4 + \dfrac{74088}{9261} = 12 > 0.$$

Therefore, $x = 21$ is a local min. Since it's the only critical point, it's an absolute min.

Example. A rectangular box with no top has two identical partitions separated by a common wall. Each partition has a square bottom. If 2400 square inches of cardboard are used with no waste to construct the box, what dimensions yield the box with the largest (total) volume?

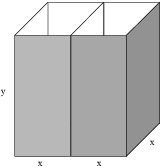
$$\hbox{\epsfysize=1.5in \epsffile{max-min-word-problems-10.eps}}$$

Suppose the base of each partition is x by x and the height is y. The volume is

$$V = 2 x^2 y.$$

The area of the bottom is $2 x^2$ , the area of the front is $2 x y$ , the area of the back is $2 x y$ , the area of the left side is $x y$ , the area of the right side is $x y$ , and the area of the divider that separates the two partitions is $x y$ . The total area is

$$2 x^2 + 2 x y + 2 x y + x y + x y + x y = 2400, \quad\hbox{so}\quad 2 x^2 + 7 x y = 2400.$$

Solving for y yields $y = \dfrac{2400 - 2 x^2}{7 x}$ . Plug this into the volume equation and simplify:

$$V = 2 x^2 \cdot \dfrac{2400 - 2 x^2}{7 x} = \dfrac{2}{7} x (2400 - 2 x^2) = \dfrac{2}{7} (2400 x - 2 x^3).$$

x can't be 0, since $x = 0$ causes division by 0 in the formula for y. Since x is a length, it must be positive. So $x > 0$ , and there is no other restriction on x. Since x is not restricted to a closed interval $[a, b]$ , I'll use the Second Derivative Test.

Differentiate:

$$V' = \dfrac{2}{7} (2400 - 6 x^2),$$

$$V'' = \dfrac{2}{7} (-12 x) = -\dfrac{24}{7} x.$$

Find the critical points by setting $V' = 0$ :

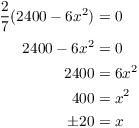
$$\eqalign{ \dfrac{2}{7} (2400 - 6 x^2) & = 0 \cr \noalign{\vskip2pt} 2400 - 6 x^2 & = 0 \cr 2400 & = 6 x^2 \cr 400 & = x^2 \cr \pm 20 & = x \cr}$$

Since x must be positive, I get $x = 20$ . This gives

$$y = \dfrac{2400 - 800}{140} = \dfrac{80}{7}.$$

Plug $x = 20$ into $V''$ :

$$V'' = -\dfrac{24}{7} \cdot 20 = -\dfrac{480}{7} < 0.$$

Hence, $x = 20$ is a local max. Since it's the only critical point, it's an absolute max.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga