The Mean Value Theorem

A secant line is a line drawn through two points on a curve.

The Mean Value Theorem relates the slope of a secant line to the slope of a tangent line.

Theorem. (The Mean Value Theorem) If f is continuous on $a \le x \le b$ and differentiable on $a < x < b$ , there is a number c in $a < x < b$ such that

$$\dfrac{f(b) - f(a)}{b - a} = f'(c).$$

I won't give a proof here, but the picture below shows why this makes sense. I've drawn a secant line through the points $(a,f(a))$ and $(b,f(b))$ . The Mean Value Theorem says that somewhere in between a and b, there is a point c on the curve where the tangent line has the same slope as the secant line.

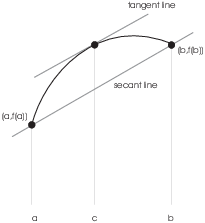
$$\hbox{\epsfysize=2in \epsffile{mean-value-theorem1.eps}}$$

Lines with the same slope are parallel. To find a point where the tangent line is parallel to the secant line, take the secant line and "slide" it (without changing its slope) until it's tangent to the curve.

If you experiment with some curves, you'll find that it's always possible to do this (provided that the curve is continuous and differentiable as stipulated in the theorem).

Example. For the function $f(x) = x^3 + 3 x^2$ on the interval $-5 \le x \le 1$ , find a number (or numbers) satisfying the conclusion of the Mean Value Theorem.

Since f is a polynomial, f is continuous on $-5 \le x \le 1$ and differentiable on $-5 < x < 1$ . Moreover,

$$\dfrac{f(1) - f(-5)}{1 - (-5)} = \dfrac{4 - (-50)}{1 - (-5)} = 9.$$

Hence, there is a number c --- maybe more than one --- between -5 and 1 such that $f'(c) = 9$ . I'll try to find one.

$f'(x) = 3 x^2 + 6 x$ , so $f'(c) = 3 c^2 + 6 c$ . Set $f'(c)$ equal to 9 and solve for c:

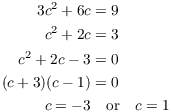
$$\eqalign{ 3 c^2 + 6 c & = 9 \cr c^2 + 2 c & = 3 \cr c^2 + 2 c - 3 & = 0 \cr (c + 3)(c - 1) & = 0 \cr c = -3 & \quad\hbox{or}\quad c = 1 \cr}$$

$c = 1$ is not in the interval $-5 < x < 1$ --- it's an endpoint --- but $c = -3$ is. $c = -3$ is a number satisfying the conclusion of the Mean Value Theorem.

Remark. It's common for mathematicians to say "there is a number" as short for "there is at least one number". So the Mean Value Theorem should be interpreted to mean "there is at least one number c" satisfying the conclusion of the theorem. There could be many numbers which work --- even an infinite number of them!

Also, finding a value of c that works may be difficult. But the theorem only guarantees that such a c exists, not that you'll be able to find it.

Example. Consider $f(x) = \dfrac{1}{x^2}$ on the interval $-1 \le x \le 1$ . Then

$$\dfrac{f(1) - f(-1)}{1 - (-1)} = 0.$$

However, $f'(x) = -\dfrac{2}{x^3}$ , and $f'(c) = -\dfrac{2}{c^3} = 0$ has no solution. Why doesn't this contradict the Mean Value Theorem? This does not contradict the Mean Value Theorem, because f is undefined at $x = 0$ , which is in the middle of the interval $-1 \le x \le 1$ .

Example. Calvin Butterball runs a 100 yard dash in 20 seconds. Assume that the function $s(t)$ which gives his position relative to the starting line is continuous and differentiable. Show that Calvin must have been running at 5 yards per second at some point during his run.

When $t = 0$ , he's at the starting line, so $s = 0$ . When $t = 20$ , he's at the finish line, so $s = 100$ . Applying the Mean Value Theorem to s for $0 \le t \le 20$ , I find that there is a point c between 0 and 20 such that

$$s'(c) = \dfrac{100 - 0}{20 - 0} = 5.$$

That is, Calvin's velocity at $t = c$ was 5 yards per second, which is what I wanted to show.

You know that the derivative of a constant is zero. The Mean Value Theorem can be used to show that the converse is also true.

Theorem. If f is continuous on the closed interval $a \le x \le b$ and $f'(x) = 0$ for all x in the open interval $a < x < b$ , then f is constant on the closed interval $a \le x \le b$ .

Proof. Let d be any number such that $a < d \le b$ . The Mean Value Theorem applies to f on the interval $a \le x \le d$ , so there is a number c such that $a < c < d$ and

$$\dfrac{f(d) - f(a)}{d - a} = f'(c).$$

By assumption, $f'(c) = 0$ . Therefore,

$$\eqalign{ \dfrac{f(d) - f(a)}{d - a} & = 0 \cr \noalign{\vskip2pt} f(d) - f(a) & = 0 \cr f(d) & = f(a) \cr}$$

Since d was an aribtrary number such that $a < d \le b$ , it follows that $f(a) = f(x)$ for all x in $a \le x \le b$ . This means that f is constant on the interval.

We'll use this idea when we discuss antiderivatives. Here's a sketch of the idea.

I know that

$$\der {} x x^3 = 3 x^2.$$

If $f(x)$ is any other function such that $\der {} x f(x) = 3 x^2$ , then

$$\der {} x \left(f(x) - x^3\right) = 3 x^2 - 3 x^2 = 0.$$

By the theorem, $f(x) - x^3 = c$ , where c is a constant. Therefore, $f(x) = x^3 + c$ . In other words, the only functions whose derivatives are $3 x^2$ are functions like

$$x^3, \quad x^3 + 13, \quad x^3 - \sqrt{7}, \quad\hbox{and so on}.$$

When I discuss antiderivatives, I'll express this fact by writing

$$\int 3 x^2\,dx = x^3 + c.\quad\halmos$$

Corollary. ( Rolle's Theorem) Suppose f is continuous on $a \le x \le b$ and differentiable on $a < x < b$ , and in addition that $f(a) = f(b)$ . Then there is a number c in $a < x < b$ such that

$$f'(c) = 0.$$

Proof. Apply the Mean Value Theorem to get

$$\dfrac{f(b) - f(a)}{b - a} = f'(c).$$

But $f(a) = f(b)$ , so $f(b) - f(a) = 0$ , and the left side is 0 --- which gives the conclusion of Rolle's Theorem.

A particular case where the hypothesis $f(a) = f(b)$ holds is when a and b are roots of f, since then

$$f(a) = f(b) = 0.$$

In this situation, Rolle's Theorem says that there is at least one horizontal tangent between every pair of roots.

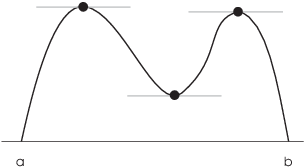
$$\hbox{\epsfysize=1.5in \epsffile{mean-value-theorem2.eps}}$$

In the picture above, there are three critical points between the roots at a and b.

Example. By the Mean Value Theorem, the function $f(x) = x(x - 20)(x - 200)(x - 2000)$ has critical points --- places where $f' = 0$ --- between 0 and 20, between 20 and 200, and between 200 and 2000.

Example. Prove that the function $f(x) = x^5 + 7 x^3 + 13 x - 18$ has exactly one root.

Step 1. Since $f(10) = 107112$ and $f(-10) = -107148$ , and since f is continuous, the Intermediate Value Theorem implies that there is a root between -10 and 10. Thus, f has at least one root.

Step 2. Suppose that f has more than one root. Suppose, in particular, that a and b are two roots of f.

By Rolle's theorem, f must have a horizontal tangent between a and b. That is, $f'(c) = 0$ for $a < c < b$ .

However, the derivative is $f'(x) = 5 x^4 + 21 x^2 + 13$ . Since even powers are nonnegative, $f'(x) > 0$ for all x. This contradicts $f'(c) = 0$ .

This contradiction shows that there can't be two roots, so there can't be more than one root.

Step 1 shows that there's at least one root. Step 2 shows there can't be more than one. Therefore, there must be exactly one root.

Definition. A function f is strictly increasing on an interval $a < x < b$ if for all p and q such that $a < p < q < b$ ,

$$f(p) < f(q).$$

If the last inequality is replaced with $f(p) \le f(q)$ , then f is increasing.

A function f is strictly decreasing on an interval $a < x < b$ if for all p and q such that $a < p < q < b$ ,

$$f(p) > f(q).$$

If the last inequality is replaced with $f(p) \ge f(q)$ , then f is decreasing.

Proposition. Suppose f is differentiable on $a < x < b$ .

(a) If $f'(x) > 0$ on $a < x < b$ , then f is strictly increasing on $a < x < b$ .

(b) If $f'(x) < 0$ on $a < x < b$ , then f is strictly decreasing on $a < x < b$ .

Proof. Take p and q between a and b; say $a < p < q < b$ . I want to show $f(p) < f(q)$ . By the Mean Value Theorem, there is a number c such that $p < c < q$ and

$$\dfrac{f(q) - f(p)}{q - p} = f'(c).$$

But $f'(c) > 0$ , so

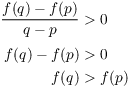
$$\eqalign{ \dfrac{f(q) - f(p)}{q - p} & > 0 \cr \noalign{\vskip2pt} f(q) - f(p) & > 0 \cr f(q) & > f(p) \cr}$$

This proves that f is strictly increasing on the interval.

The proof for (b) is similar.

Remark. In (a) if you assume instead that $f'(x) \ge 0$ on $a < x < b$ , then the same proof shows that f is increasing on $(a, b)$ . Likewise, in (b) if you assume that $f'(x) \le 0$ on $a < x < b$ , then f is decreasing on $(a, b)$ .

Example. Prove that if $0 < k < \dfrac{\pi}{2}$ , then

$$\tan k \ge k.$$

Apply the Mean Value Theorem to $f(x) = \tan x$ on the interval $0 \le x \le k$ , where $k < \dfrac{\pi}{2}$ . Then for some c between 0 and k,

$$\dfrac{\tan k - \tan 0}{k - 0} = (\sec c)^2.$$

Now $(\sec c)^2 \ge 1$ and $\tan 0 = 0$ , so

$$\dfrac{\tan k}{k} \ge 1 \quad\hbox{and hence}\quad \tan k \ge k.$$

A picture which illustrates this (not to scale) follows:

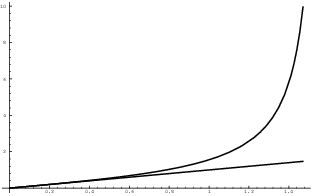
$$\hbox{\epsfysize=1.75in \epsffile{mean-value-theorem3.eps}}$$

The curve is the graph of $y = \tan x$ and the line is $y = x$ . You can see that the curve appears to lie above the line.

Example. ( Using the Mean Value Theorem to estimate a function value) Suppose that f is a differentiable function,

$$f(3) = 2, \quad\hbox{and}\quad 3 \le f'(x) \le 4 \quad\hbox{for all}\quad x.$$

Prove that $8 \le f(5) \le 10$ .

Apply the Mean Value Theorem to f on the interval $3 \le x \le 5$ :

$$\dfrac{f(5) - f(3)}{5 - 3} = f'(c) \quad\hbox{where}\quad 3 < c < 5.$$

Then since $3 \le f'(c) \le 4$ , I have

$$\matrix{3 & \le & \dfrac{f(5) - f(3)}{5 - 3} & \le & 4 \cr 3 & \le & \dfrac{f(5) - 3}{2} & \le & 4 \cr 6 & \le & f(5) - 3 & \le & 8 \cr 8 & \le & f(5) & \le & 10 \quad\halmos \cr}$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga