The Natural Logarithm

In earlier courses, you may have seen logarithms defined in terms of raising bases to powers. For example,

$$\log_2 8 = 3 \quad\hbox{because}\quad 2^3 = 8.$$

In those terms, the natural logarithm $\ln x = \log_e x$ should be the power to which you raise e to get x. (Remember that $\ln x$ is just shorthand for $\log_e x$ .)

Now

$$e = 2.718281828459045 \ldots.$$

e is represented by an infinite non-repeating decimal (like $\pi$ ). So, for instance, $\ln 4$ is the power to which you raise $e = 2.718281828459045 \ldots$ to get 4. How would you figure that out?

You might also wonder where e comes from: How do you compute it? And why choose such an ugly number for a logarithm base?

In this section, I'll take a different approach to the natural log. I'll define it using calculus as the area under a curve. For starters, this allows us to compute its derivative easily. But what does this have to do with logarithms defined in terms of raising bases to powers?

When you studied logarithms, you learned that they satisfy certain properties:

(a) $\log_a x y = \log_a x + \log_a y$ .

(b) $\log_a \dfrac{x}{y} = \log_a x - \log_a y$ .

(c) $\log_a x^p = p \log_a x$ .

(d) $\log_a 1 = 0$ .

I'll show that the log I define as an area satisfies those properties. That gives some justification for considering it to be a "logarithm".

To begin with, the Power Rule says

$$\int x^n\,dx = \dfrac{1}{n + 1}x^{n+1} + C \quad\hbox{for}\quad n \ne -1.$$

The formula does not apply to

$$\int \dfrac{1}{x}\,dx.$$

An antiderivative $F(x)$ of $\dfrac{1}{x}$ would have to satisfy

$$\der {} x F(x) = \dfrac{1}{x}.$$

But the Fundamental Theorem implies that if $x > 0$ , then

$$\der {} x \int_1^x \dfrac{1}{t}\,dt = \dfrac{1}{x}.$$

Thus, $\displaystyle \int_1^x \dfrac{1}{t}\,dt$ plays the role of $F(x)$ .

Define the natural log function $\ln x$ by

$$\ln x = \int_1^x \dfrac{1}{t}\,dt \quad\hbox{for}\quad x > 0.$$

By construction, if $x > 0$ ,

$$\der {} x \ln x = \dfrac{1}{x}, \quad\hbox{and}\quad \int \dfrac{1}{x}\,dx = \ln x + C.$$

$\displaystyle \int_1^x \dfrac{1}{t}\,dt$ represents the area under $f(t) = \dfrac{1}{t}$ from 1 to x:

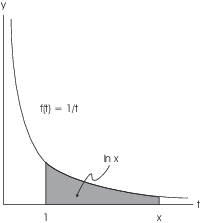
$$\hbox{\epsfysize=2in \epsffile{natural-logarithm-1.eps}}$$

$\ln x$ has many properties you'd expect a logarithm to have. For example,

$$\ln 1 = \int_1^1 \dfrac{1}{t}\,dt = 0.$$

You'd expect the log of a product to equal the sum of the logs. If a and b are positive numbers, then

$$\ln (a b) = \int_1^{a b} \dfrac{1}{t}\,dt = \int_1^a \dfrac{1}{t}\,dt + \int_a^{a b} \dfrac{1}{t}\,dt.$$

In the second integral, let $u = \dfrac{t}{a}$ , so $du = \dfrac{dt}{a}$ , and $dt = a\,du$ . When $t = a$ , $u = 1$ ; when $t = a b$ , $u = b$ . So

$$\int_1^a \dfrac{1}{t}\,dt + \int_a^{a b} \dfrac{1}{t}\,dt = \int_1^a \dfrac{1}{t}\,dt + \int_1^b \dfrac{1}{u}\,du = \ln a + \ln b.$$

In other words,

$$\ln (a b) = \ln a + \ln b.$$

In similar fashion, you can verify that

$$\ln \dfrac{a}{b} = \ln a - \ln b \quad\hbox{and}\quad \ln x^p = p \ln x.$$

Thus, there is some justification in calling $\ln x$ a logarithm, because it has the same properties you'd expect logs to have.

Here are some additional properties of $\ln x$ .

First,

$$\der {} x \ln x = \dfrac{1}{x} > 0 \quad\hbox{for}\quad x > 0.$$

Therefore, the graph of $\ln x$ is increasing for $x > 0$ .

Moreover,

$$\dfrac{d^2}{dx^2} \ln x = -\dfrac{1}{x^2} < 0 \quad\hbox{for}\quad x > 0.$$

Therefore, the graph of $\ln x$ is concave down for $x > 0$ .

Next, consider the following picture:

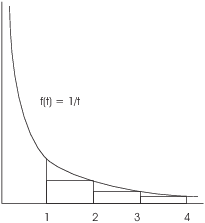
$$\hbox{\epsfysize=2in \epsffile{natural-logarithm-2.eps}}$$

The area under the curve from 1 to 4 is $\ln 4$ . It is greater than the sum of the areas of the three rectangles, so

$$\ln 4 > \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} = \dfrac{13}{12} > 1.$$

If n is a positive integer, then

$$n \ln 4 > n, \quad\quad\hbox{or}\quad\quad \ln 4^n > n.$$

So if $x > 4^n$ , then

$$\ln x > \ln 4^n > n.$$

Since n is an arbitrary positive integer, I can make $\ln x$ arbitrarily large by making x sufficiently large. This proves that

$$\lim_{x \to +\infty} \ln x = +\infty.$$

Here's the graph of $\ln x$ :

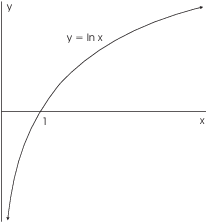
$$\hbox{\epsfysize=2in \epsffile{natural-logarithm-3.eps}}$$

The differentiation formula for $\ln x$ works together with the other differentiation rules in the usual ways.

Example. Compute:

(a) $\der {} x \ln (x^2 + x + 7)$ .

(b) $\der {} x \ln (\sin x + x^3)$ .

(c) $\der {} x \left[(\ln x)^7 + \ln (x^7)\right]$ .

(d) $\der {} x \dfrac{x^2}{\ln x}$ .

(e) $\der {} x \ln \left(\ln \left(\ln x + 1\right)\right)$ .

(a)

$$\der {} x \ln (x^2 + x + 7) = \dfrac{2 x + 1}{x^2 + x + 7}.\quad\halmos$$

(b)

$$\der {} x \ln (\sin x + x^3) = \dfrac{\cos x + 3 x^2}{\sin x + x^3}.$$

(c)

$$\der {} x \left[(\ln x)^7 + \ln (x^7)\right] = \der {} x \left[(\ln x)^7 + 7 \ln x\right] = 7 (\ln x)^6 \cdot \dfrac{1}{x} + \dfrac{7}{x}.\quad\halmos$$

(d)

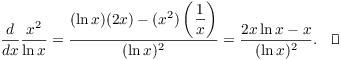
$$\der {} x \dfrac{x^2}{\ln x} = \dfrac{(\ln x)(2 x) - (x^2)\left(\dfrac{1}{x}\right)}{(\ln x)^2} = \dfrac{2 x \ln x - x}{(\ln x)^2}.\quad\halmos$$

(e)

$$\der {} x \ln \left(\ln \left(\ln x + 1\right)\right) = \left(\dfrac{1}{\ln \left(\ln x + 1\right)}\right) \left(\dfrac{1}{\ln x + 1}\right)\left(\dfrac{1}{x}\right). \quad\halmos$$

If I say that "$\der {} x f(x) = g(x)$ " --- the derivative of $f(x)$ is $g(x)$ --- then $g(x)$ should be defined wherever $f(x)$ is defined. Therefore, it is not really correct to say without the qualification $x > 0$ that "$\der {} x \ln x = \dfrac{1}{x}$ ". For $\dfrac{1}{x}$ is defined for $x \ne 0$ , whereas $\ln x$ is only defined for $x > 0$ .

It turns out that the correct statement is:

$$\der {} x \ln |x| = \dfrac{1}{x} \quad\hbox{for}\quad x \ne 0.$$

For $x > 0$ , this is the same as the old formula. For $x < 0$ , $|x| = -x$ , so

$$\der {} x \ln |x| = \der {} x \ln (-x) = \dfrac{-1}{-x} = \dfrac{1}{x}.$$

So our new antiderivative formula is

$$\int \dfrac{1}{x}\,dx = \ln |x| + C.$$

You can omit the absolute value signs if the quantity inside is never negative. For example,

$$\int \dfrac{2 x}{x^2 + 1}\,dx = \ln (x^2 + 1) + C.$$

Since $x^2 + 1$ is always positive, I can write "$\ln (x^2 + 1)$ " instead of "$\ln |x^2 + 1|$ ".

Example. Compute $\displaystyle \int \dfrac{dx}{2 x - 5}$ .

$$\int \dfrac{dx}{2 x - 5} = \int \dfrac{1}{u} \dfrac{du}{2} = \dfrac{1}{2} \int \dfrac{1}{u}\,du = \dfrac{1}{2} \ln |u| + C = \dfrac{1}{2} \ln |2 x - 5| + C.$$

$$\left[u = 2 x - 5, \quad du = 2\,dx, \quad dx = \dfrac{du}{2}\right]\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{x^2}{x^3 + 2}\,dx$ .

$$\int \dfrac{x^2}{x^3 + 2}\,dx = \int \dfrac{x^2}{u} \dfrac{du}{3 x^2} = \dfrac{1}{3} \int \dfrac{1}{u}\,du = \dfrac{1}{3} \ln |u| + C = \dfrac{1}{3} \ln |x^3 + 2| + C.$$

$$\left[u = x^3 + 2, \quad du = 3 x^2\,dx, \quad dx = \dfrac{du}{3 x^2}\right]\quad\halmos$$

You can use logarithmic differentiation to compute derivatives which are difficult to compute in other ways.

Example. Compute $\der {} x (x^2 + 1)^{x^4}$ .

Let $y = (x^2 + 1)^{x^4}$ . Taking logs and bringing the power down, I get

$$\ln y = \ln (x^2 + 1)^{x^4} = x^4 \ln (x^2 + 1).$$

Differentiate both sides, using the Chain Rule on the left and the Product Rule (and Chain Rule) on the right:

$$\dfrac{y'}{y} = (x^4)\left(\dfrac{2 x}{x^2 + 1}\right) + [\ln (x^2 + 1)](4 x^3).$$

Multiply both sides by y to clear the fraction on the left, then substitute $y = (x^2 + 1)^{x^4}$ :

$$y' = y \left((x^4)\left(\dfrac{2 x}{x^2 + 1}\right) + [\ln (x^2 + 1)](4 x^3)\right) = (x^2 + 1)^{x^4}\left((x^4)\left(\dfrac{2 x}{x^2 + 1}\right) + [\ln (x^2 + 1)](4 x^3)\right).\quad\halmos$$

I can use calculus to construct the exponential function $e^x$ .

For $x > 0$ , I have

$$\der {} x \ln x = \dfrac{1}{x}.$$

Since $x > 0$ , I have $\der {} x \ln x = \dfrac{1}{x} > 0$ . This means that $\ln x$ increases for $x > 0$ . Next, I use following facts:

(a) An increasing function f is injective: If $f(a) = f(b)$ , then $a = b$ .

(b) An injective function $f: X \to Y$ has an inverse function $f^{-1}: Y \to X$ .

Applying these facts to $\ln x$ , I find that it has an inverse function, which I will denote $e^x$ (or $\exp (x)$ ). Thus:

1. $e^x$ is a function from $\real$ to the positive real numbers (because $\ln x$ is a function from the positive real numbers to $\real$ ).

2. $e^{\ln x} = x$ for $x > 0$ and $\ln e^x = x$ for $x \in \real$ .

It's easy to use the properties of the natural log to derive corresponding properties of $e^x$ :

(a) $e^{x + y} = e^x \cdot e^y$ .

(b) $e^{x - y} = \dfrac{e^x}{e^y}$ .

(c) $(e^x)^p = e^{x p}$ .

(d) $e^0 = 1$ .

To complete the discussion, I can use $\ln x$ and $e^x$ to define logs and exponentials to other bases.

(a) If $a > 0$ and $x > 0$ , define $\log_a x = \dfrac{\ln x}{\ln a}$ .

(b) If $a > 0$ , define $a^x = e^{x \ln a}$ .

With these definitions,

$$a^{\log_a x} = a^{(\ln x)/(\ln a)} = e^{(\ln x)/(\ln a) \cdot \ln a} = e^{\ln x} = x.$$

In words, this says that $\log_a x$ is the power to which you raise a to get x --- the definition of a log in terms of a base raised to a power that you knew before.

Using the definitions for $\log_a x$ and $a^x$ , I also get the differentiation formulas

$$\der {} x \log_a x = \dfrac{1}{x \ln a} \quad\hbox{and}\quad \der {} x a^x = a^x \ln a.$$

The point of doing things using calculus is not that we have any new properties. Rather, it allows us to derive properties which were just stated and taken for granted in a rigorous way.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga