Rectangle Sums

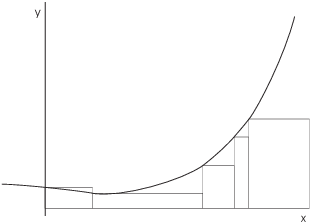
You can approximate the area under a curve using rectangles. To do this, divide the base interval into pieces ( subintervals). Then on each subinterval, build a rectangle that goes up to the curve.

$$\hbox{\epsfysize=2in \epsffile{rectangle-sums-1.eps}}$$

What does it mean to "go up to the curve"? You have to make a choice about how the height of each rectangle depends on the curve. In the picture above, for my rectangle height I always used the height of the curve above the left-hand endpoint of each subinterval.

In the picture above, I used subintervals of different sizes. For simplicity, you will often use subintervals of the same size --- so your rectangles all have the same width. In the picture below, I've used 8 rectangles of equal widths, and for my rectangle height I always used the height of the curve above the right-hand endpoint of each subinterval.

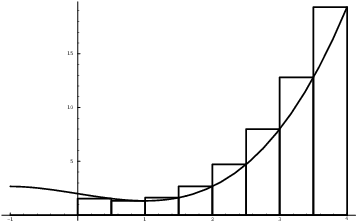
$$\hbox{\epsfysize=2in \epsffile{rectangle-sums-2.eps}}$$

Here's an example with a specific function. I'll use $f(x) = \sin (x^2)$ . In each case, I'll use the base interval $0 \le x \le 1.5$ divided into 6 equal subintervals:

$$[0, 0.25], [0.25, 0.5], [0.5, 0.75], [0.75, 1.0], [1.0, 1.25], [1.25, 1.5]$$

Here is the picture if I use the left-hand endpoint of each subinterval to get the height of each rectangle:

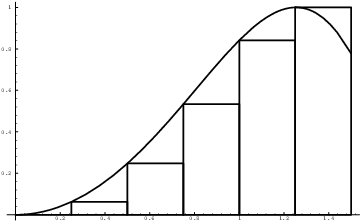
$$\hbox{\epsfysize=2in \epsffile{rectangle-sums-3.eps}}$$

The sum of the areas of the rectangles is:

$$\left(\sin 0\right)(0.25) + \left(\sin \dfrac{1}{16}\right)(0.25) + \left(\sin \dfrac{1}{4}\right)(0.25) + \left(\sin \dfrac{9}{16}\right)(0.25) + \left(\sin 1\right)(0.25) + \left(\sin \dfrac{25}{16}\right)(0.25) =$$

$$\left(\sin 0 + \sin \dfrac{1}{16} + \sin \dfrac{1}{4} + \sin \dfrac{9}{16} + \sin 1 + \sin \dfrac{25}{16}\right)(0.25) \approx 0.671151.$$

Notice that the rectangle width 0.25 factors out of the sum --- you add up the f's, then multiply by 0.25. This will always be possible if you use subintervals of equal length.

Here is the picture if I use the right-hand endpoint of each subinterval to get the height of each rectangle:

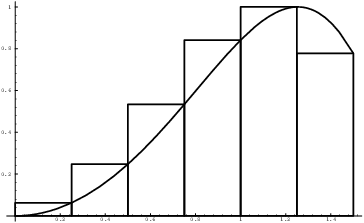
$$\hbox{\epsfysize=2in \epsffile{rectangle-sums-4.eps}}$$

In this case, the sum of the areas of the rectangles is

$$\left(\sin \dfrac{1}{16}\right)(0.25) + \left(\sin \dfrac{1}{4}\right)(0.25) + \left(\sin \dfrac{9}{16}\right)(0.25) + \left(\sin 1\right)(0.25) + \left(\sin \dfrac{25}{16}\right)(0.25) + \left(\sin \dfrac{9}{4}\right)(0.25) =$$

$$\left(\sin \dfrac{1}{16} + \sin \dfrac{1}{4} + \sin \dfrac{9}{16} + \sin 1 + \sin \dfrac{25}{16} + \sin \dfrac{9}{4}\right)(0.25) \approx 0.865669.$$

Here is the picture if I use the midpoint of each subinterval to get the height of each rectangle:

$$\hbox{\epsfysize=2in \epsffile{rectangle-sums-5.eps}}$$

The midpoints of the subintervals are:

$$0.125, 0.375, 0.625, 0.875. 1.125, 1.375$$

In this case, the sum of the areas of the rectangles is

$$\left(\sin \dfrac{1}{64}\right)(0.25) + \left(\sin \dfrac{9}{64}\right)(0.25) + \left(\sin \dfrac{25}{64}\right)(0.25) + \left(\sin \dfrac{49}{64}\right)(0.25) + \left(\sin \dfrac{81}{64}\right)(0.25) + \left(\sin \dfrac{121}{64}\right)(0.25) =$$

$$\left(\sin \dfrac{1}{64} + \sin \dfrac{9}{64} + \sin \dfrac{25}{64} + \sin \dfrac{49}{64} + \sin \dfrac{81}{64} + \sin \dfrac{121}{64}\right)(0.25) \approx 0.783156.$$

By comparison, the actual area under the curve is around 0.778238.

You can get better approximations by taking more rectangles. For example, here is the left-hand endpoint picture with 50 rectangles:

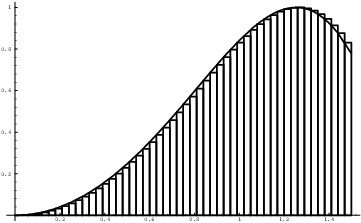
$$\hbox{\epsfysize=2in \epsffile{rectangle-sums-6.eps}}$$

Notice how much better the rectangles approximate the area under the curve.

With 200 rectangles, the left-hand endpoint sum is 0.775311, the right-hand endpoint sum is 0.781147, and the midpoint sum is 0.778242. The three values are close to the actual value 0.778238.

Example. Approximate the area under $f(x) = 4 - x^2$ for $0 \le x \le 2$ , using 20 circumscribed rectangles of equal width.

Circumscribed means that you should use the largest function value on each interval to get the height of a rectangle. My subintervals are

$$[0,0.1], [0.1,0.2], [0.2,0.3], \ldots, [1.9,2.0].$$

In general, it can be difficult to determine where the largest function value is. However, by graphing $f(x) = 4 - x^2$ on $0 \le x \le 2$ , you can see that the largest function value for each subinterval occurs at the left-hand endpoint.

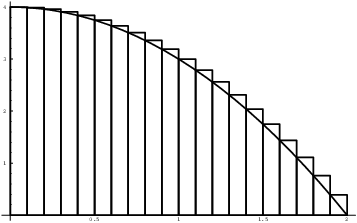
$$\hbox{\epsfysize=2in \epsffile{rectangle-sums-7.eps}}$$

So I use

$$0 \quad\hbox{for the first subinterval},$$

$$0.1 \quad\hbox{for the second subinterval},$$

$$0.2 \quad\hbox{for the third subinterval}.$$

I continue in this fashion, all the way up to

$$1.9 \quad\hbox{for the twentieth subinterval}.$$

I can write these points as

$$0.1n, \quad\hbox{for}\quad n = 0, 1, \ldots, 19.$$

So my function values are

$$f(0), f(0.1), f(0.2), \ldots, f(1.9).$$

These are the rectangles heights. Each height is multiplied by a width of 0.1. The total is

$$f(0)\cdot 0.1 + f(0.1)\cdot 0.1 + f(0.2)\cdot 0.1 + \cdots + f(1.9)\cdot 0.1 = \sum_{n=0}^{19} f(0.1n)\cdot 0.1 =$$

$$\sum_{n=0}^{19} \left(4 - (0.1n)^2\right)\cdot 0.1 = \sum_{n=0}^{19} (0.4 - 0.001n^2).$$

Now the sum is in a form you can evaluate on your calculator. You should get 5.53; the actual value is $5.33333 \ldots$ .

Example. Approximate the area under $y = \dfrac{1}{1 + x^3}$ from $x = 0$ to $x = 1$ using 20 equal subintervals and evaluating the function at the left-hand endpoints.

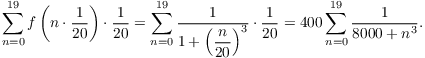
$$\sum_{n=0}^{19} f\left(n\cdot \dfrac{1}{20}\right) \cdot \dfrac{1}{20} = \sum_{n=0}^{19} \dfrac{1}{1 + \left(\dfrac{n}{20}\right)^3} \cdot \dfrac{1}{20} = 400 \sum_{n=0}^{19} \dfrac{1}{8000 + n^3}.$$

You can use a calculator to approximate this sum; it's around 0.84799.

In the preceding examples, I've assumed that the subintervals (which give the widths of the rectangle) are the same size. I've also chosen the evaluation points systematically --- left-hand endpoints, right-hand endpoints, midpoints. These are conveniences to make setting up the computations simple.

In general, the subintervals don't have to be the same size, and I don't have to choose the evaluation points systematically. For example, here is an approximation to the area under $y = x^2$ from $x = 0$ to $x = 6$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & interval & & x & & $f(x)$ & & $f(x)\cdot\Delta x$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $[0,2]$ & & 1.0 & & 1.0 & & 2.0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $[2,3]$ & & 2.8 & & 7.84 & & 7.84 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $[3,3.5]$ & & 3.0 & & 9.0 & & 4.5 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $[3.5,6]$ & & 5.0 & & 25.0 & & 37.5 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & sum & & & & & & 51.84 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

This gives an approximate area of 51.84. The actual area is 77.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga