Related Rates

Related rates problems deal with situations in which several things are changing at rates which are related. The way in which the rates are related often arises from geometry, for example.

Example. The radius of a circle increases at 2 light-years per fortnight. At what rate is the area increasing when the radius is 3 light-years?

The area of a circle is $A = \pi r^2$ , where r is the radius. Differentiate this equation with respect to t:

$$\der A t = 2 \pi r \der r t.$$

I want to know the rate of change of the area, which is $\der A t$ .

The rate at which the radius increases is $\der r t$ , so $\der r t = 2$ . I want to find $\der A t$ when $r = 3$ . Plug in:

$$\der A t = 2 \pi \cdot 3 \cdot 2 = 12 \pi = 37.69911 \ldots.$$

The units should be square light-years per fortnight.

Notice that I don't plug $r = 3$ into the equation $A = \pi r^2$ . I differentiate first, then plug in.

In most related rates problems, you will perform the steps above: Differentiate a starting equation with respect to t (time), then plug in and answer the question. In most cases, the difficult part of the problem is obtaining the starting equation.

Before I give some examples involving real-world situations, I'll do an example which just illustrates the kind of mathematics that is involved.

Example. x and y are functions of t, and are related by

$$x^3 y - 3 y = y^2 + \dfrac{1}{y} + x - 2.$$

Find the rate at which x is changing when $x = 2$ and $y = 1$ , if y is decreasing at 3 units per second.

I differentiate the given equation with respect to t. To save writing, I'll use $x'$ to denote $\der x t$ and $y'$ to denote $\der y t$ .

$$(x^3 y' + y \cdot 3 x^2 x') - 3 y' = 2 y y' - \dfrac{1}{y^2} y' + x'. \eqno{(*)}$$

Here's how I got some of the terms.

$x^3 y$ is a product, so I applied the Product Rule to get $x^3 y' + y \cdot 3 x^2 x'$ . Note that the derivative of y is $\der y t = y'$ , and by the Chain Rule, the derivative of $x^3$ is

$$\der {} t x^3 = 3 x^2 \der x t = 3 x^2 x'.$$

I differentiated $y^2$ using the Chain Rule:

$$\der {} y y^2 = 2 y \der y t = 2 y y'.$$

I differentiated $\dfrac{1}{y} = y^{-1}$ using the Chain Rule:

$$\der {} t y^{-1} = -y^{-2} \der y t = -\dfrac{1}{y^2} y'.$$

I plug in $x = 2$ , $y = 1$ , and $\der y t = -3$ into (*). (Note that $\der y t$ is negative, because I was told that y is decreasing.)

$$(8)(-3) + (1)(12) \cdot x' - 3(-3) = 2(1)(-3) - \dfrac{1}{1}(-3) + x'.$$

Simplify and solve for $x'$ :

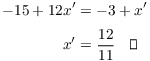
$$\eqalign{ -15 + 12 x' & = -3 + x' \cr \noalign{\vskip2pt} x' & = \dfrac{12}{11} \quad\halmos \cr}$$

Example. Calvin and Phoebe elope in a hot air balloon, which rises at a constant rate of 3 meters per second. Five seconds after they cast off, Phoebe's jilted suitor Bonzo McTavish races up in his Porsche. He parks 50 meters from the launch pad, and runs toward the pad at 2 meters per second. At what rate is the distance between Bonzo and the balloon changing when the balloon is 30 meters above the ground?

Here's a picture:

$$\hbox{\epsfysize=2.5in \epsffile{related-rates-1.eps}}$$

The triangle is a right triangle, and I've labelled the three sides with variables. x is the distance from Bonzo to the launch pad, y is the height of the balloon, and s is the distance from Bonzo to the balloon. I use variables because the three sides are changing with time: The balloon rises (y changes), Bonzo runs toward the launch pad (x changes), and the distance between Bonzo and the balloon (s) changes.

There is an obvious relationship among the variables --- Pythagoras' theorem says

$$s^2 + x^2 + y^2.$$

Differentiate with respect to t:

$$2 s \der s t = 2 x \der x t + 2 y \der y t.$$

Cancel the 2's:

$$s \der s t = x \der x t + y \der y t.$$

Now I plug in the numbers. Bonzo's velocity is $\der x t = -2$ --- negative, because the distance from Bonzo to the launch pad is decreasing. $\der y t = 3$ is the rate at which the balloon rises. I want to know what $\der s t$ is when $y = 30$ . I see that I still need x and s.

The balloon was already 15 ($3 \cdot 5$ ) meters high when Bonzo drove up. It has risen an additional $30 - 15 = 15$ meters. Since it's rising at 3 meters per second, $\dfrac{15}{3} = 5$ additional seconds elapse.

During these 5 seconds, Bonzo is running at 2 meters per second, so he travels $2\cdot 5 = 10$ meters. That leaves him $50 - 10 = 40$ meters from the launch pad. In other words, $x = 40$ .

Finally, using the equation $s^2 + x^2 + y^2$ ,

$$s = \sqrt{30^2 + 40^2} = 50.$$

Plug all this stuff into the derivatives equation:

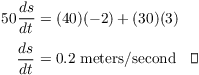
$$\eqalign{ 50 \der s t & = (40)(-2) + (30)(3) \cr \noalign{\vskip2pt} \der s t & = 0.2\ {\rm meters/second} \quad\halmos \cr}$$

Here are some rules of thumb for setting up a related rates problem:

1. Draw a picture. Be sure you've drawn it at an arbitrary instant. (In the previous example, it would be a bad idea to draw the picture with the balloon on the ground, or with Bonzo just getting out of his car.)

2. Label the quantities that are relevant to the problem. Quantities that are changing should be labelled with variables.

3. Don't put numbers on your picture unless they represent things which aren't changing.

4. Look for a relationship among the variables. Think of Pythagoras' theorem, trigonometry, area or volume formulas, and similar triangles.

5. Once you have a starting equation, differentiate with respect to t, Then plug in the given values and solve for the appropriate rate.

In the next example, I'll need the following facts from physics. The velocity of an object dropped from rest is $32 t$ feet per second after t seconds. During that t seconds, it will have fallen $16 t^2$ feet.

Example. A bowl of petunias is dropped from a point 12 feet above the ground, so that it will land 4 feet from the base of a 12 foot lamppost. At what rate is the shadow of the bowl moving along the ground when the bowl is 8 feet above the ground?

Here's a picture:

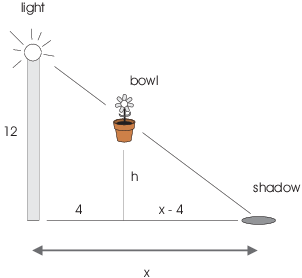
$$\hbox{\epsfysize=2.5in \epsffile{related-rates-2.eps}}$$

x is the distance from the shadow to the post. (In order to measure the rate at which the shadow is moving, I have to measure its distance to some fixed object.) h is the height of the bowl above the ground.

By similar triangles,

$$\dfrac{x - 4}{h} = \dfrac{x}{12}.$$

(Notice that if you label the picture properly, it's usually obvious what mathematical formula you should use.)

Clear denominators:

$$12 x - 48 = x h.$$

Differentiate with respect to t, being careful to use the Product Rule on the right side:

$$12 \der x t = x \der h t + h \der x t.$$

Now I plug the numbers in. I'm trying to find $\der x t$ , the rate at which the shadow is moving.

When the bowl is 8 feet above the ground, $h = 8$ , so the bowl has fallen 4 feet. By the physics fact I mentioned earlier, the bowl falls $16 t^2$ feet in t seconds; setting $16 t^2 = 4$ , I get $t = \dfrac{1}{2}$ . The bowl has been falling for $\dfrac{1}{2}$ second.

By the other physics fact I mentioned, its velocity is $32 \cdot \dfrac{1}{2} = 16$ feet per second. Thus, $\der h t = -16$ --- negative, because h is decreasing.

The only other thing I need is x. Set $h = 8$ in $12 x - 48 = x h$ :

$$12 x - 48 = 8 x, \quad x = 12.$$

Substitute x, h, and $\der h t$ :

$$\eqalign{ 12 \der x t & = (12)(-16) + 8 \der x t \cr \noalign{\vskip2pt} \der x t & = -48\ {\rm feet/second} \quad\halmos \cr}$$

Example. Calvin and Bonzo drive on long parallel roads in opposite directions at 20 feet per second and 80 feet per second, respectively. The roads are 200 feet apart. How rapidly is the distance between them changing 5 seconds after they pass one another?

Here's a picture:

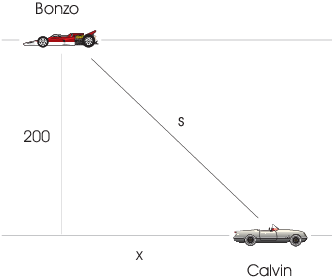
$$\hbox{\epsfysize=2.5in \epsffile{related-rates-3.eps}}$$

x is the horizontal separation between Calvin and Bonzo. s is the distance between them.

By Pythagoras,

$$s^2 = x^2 + 200^2.$$

Differentiate with respect to t:

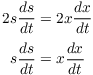
$$\eqalign{ 2 s \der s t & = 2 x \der x t \cr \noalign{\vskip2pt} s \der s t & = x \der x t \cr}$$

I want $\der s t$ .

The rate of change of the distance between them is the same as it would be if Bonzo was moving at $80 + 20 = 100$ feet per second and Calvin was stationary. So $\der x t = 100$ , and 5 second after they pass each other, $x = 5\cdot 100 = 500$ .

To find s, plug $x = 500$ into $s^2 = x^2 + 200^2$ :

$$s = \sqrt{500^2 + 200^2} = 100 \sqrt{29}.$$

Now plug everything in:

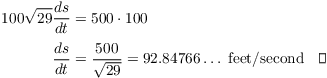
$$\eqalign{ 100 \sqrt{29} \der s t & = 500 \cdot 100 \cr \noalign{\vskip2pt} \der s t & = \dfrac{500}{\sqrt{29}} = 92.84766 \ldots\ {\rm feet/second} \quad\halmos \cr}$$

Example. A ferris wheel 50 feet in diameter makes 2 revolutions per minute. Assume that the wheel is tangent to the ground and let P be the point of tangency. At what rate is the distance between P and a rider changing, when she is 25 feet above the ground and going up?

Here's a picture:

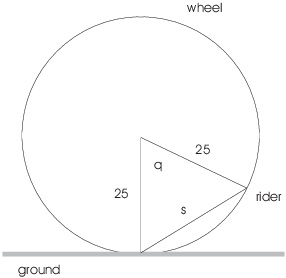
$$\hbox{\epsfysize=2.5in \epsffile{related-rates-4.eps}}$$

$\theta$ is the angle between the vertical and a radius out to the rider. s is the distance between the bottom of the wheel and the rider.

By the Law of Cosines,

$$s^2 = 25^2 + 25^2 - 2\cdot 25\cdot 25 \cos \theta.$$

Differentiate with respect to t:

$$2 s \der s t = 1250 \sin \theta \der \theta t.$$

Assuming that the wheel is turning counterclockwise in the picture, when the rider is 25 feet above the ground, she's on the far right hand side. At this point, $\theta = \dfrac{\pi}{2}$ , and $s = 25\sqrt{2}$ (since the triangle is then an isosceles right triangle).

$\der \theta t$ is the rate at which the wheel is turning. I must be careful to express this in radians per minute:

$$\der \theta t = \left(2 \dfrac{\rm rev}{\rm min}\right) \left(2 \pi \dfrac{\rm rad}{\rm rev}\right) = 4 \pi \dfrac{\rm rad}{\rm min}.$$

Plug in:

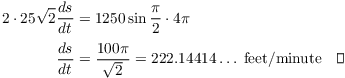
$$\eqalign{ 2 \cdot 25 \sqrt{2} \der s t & = 1250 \sin \dfrac{\pi}{2} \cdot 4\pi \cr \noalign{\vskip2pt} \der s t & = \dfrac{100 \pi}{\sqrt{2}} = 222.14414 \ldots \ {\rm feet/minute} \quad\halmos \cr}$$

Example. A spotlight on the top of a police cruiser makes one revolution per second. The spotlight is 40 feet from a long straight wall. At what rate is the spot of light moving across the wall at the instant when the beam makes a $30^\circ$ angle with the wall?

Here's a picture:

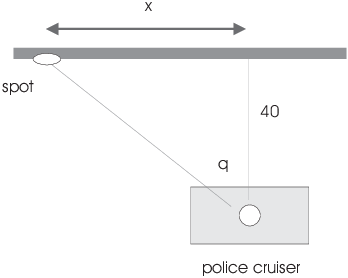
$$\hbox{\epsfysize=2.5in \epsffile{related-rates-5.eps}}$$

x is the distance from the spot to the point on the wall nearest the cruiser. $\theta$ is the angle between the beam and the altitude to the wall from the light.

By basic trigonometry,

$$\tan \theta = \dfrac{x}{40}.$$

Differentiate with respect to t:

$$(\sec \theta)^2 \der \theta t = \dfrac{1}{40} \der x t.$$

When the beam makes a $30^\circ$ angle with the wall, $\theta = 60^\circ = \dfrac{\pi}{3}$ . The rate at which the beam is turning is

$$\der \theta t = \left(1 \dfrac{\rm rev}{\rm sec}\right) \left(2 \pi \dfrac{\rm rad}{\rm rev}\right) = 2 \pi \dfrac{\rm rad}{\rm sec}.$$

Plug in:

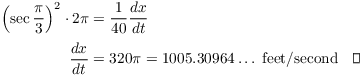
$$\eqalign{ \left(\sec \dfrac{\pi}{3}\right)^2 \cdot 2 \pi & = \dfrac{1}{40} \der x t \cr \noalign{\vskip2pt} \der x t & = 320 \pi = 1005.30964 \ldots \ {\rm feet/second} \quad\halmos \cr}$$

Example. A helium balloon is released from ground level and rises at a constant rate of 2 feet per second. Calvin stands at the top of a 100-foot observation tower located 60 feet from the point where the balloon was released. At what rate is the distance between Calvin and the balloon changing when the balloon is 55 feet above the ground?

Let y be the height of the balloon above the ground, and let r be the distance from Calvin to the balloon.

$$\hbox{\epsfysize=2in \epsffile{related-rates-6.eps}}$$

By Pythagoras,

$$60^2 + (100 - y)^2 = r^2.$$

Differentiate with respect to t:

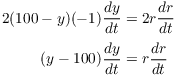
$$\eqalign{ 2 (100 - y)(-1)\der y t & = 2 r \der r t \cr \noalign{\vskip2pt} (y - 100)\der y t & = r\der r t \cr}$$

I want $\der r t$ . Now $\der y t = 2$ feet per second; when $y = 55$ ,

$$60^2 + (100 - 55)^2 = r^2, \quad r = 75.$$

Thus,

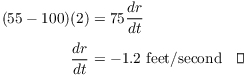
$$\eqalign{ (55 - 100)(2) & = 75 \der r t \cr \noalign{\vskip2pt} \der r t & = -1.2\ {\rm feet}/{\rm second} \quad\halmos \cr}$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga