Separation of Variables

Separation of variables is a method for solving a differential equation. I'll illustrate with some examples.

Example. Solve $\der y x = 2 x y$ .

"Solve" usually means to find y in terms of x. In general, I'll be satisfied if I can eliminate the derivative by integration.

First, I rearrange the equation to get the x's on one side and the y's on the other (separation):

$$\dfrac{dy}{y} = 2 x\,dx.$$

This is a formal manipulation, since I'm temporarily treating $\der y x$ as a quotient of $dy$ by $dx$ . (See the remark below.)

Next, I integrate both sides:

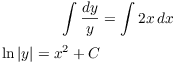
$$\eqalign{ \int \dfrac{dy}{y} & = \int 2 x\,dx \cr \noalign{\vskip2pt} \ln |y| = x^2 + C \cr}$$

I only need an arbitrary constant on one side of the equation. Finally, I solve for y in terms of x, if possible:

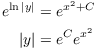
$$\eqalign{ e^{\ln |y|} & = e^{x^2+C} \cr |y| & = e^C e^{x^2} \cr}$$

Here's a convenient trick which I'll use in these situations. Think of $|y|$ as $\pm y$ . Move the $\pm$ to the other side:

$$y = \mp e^C e^{x^2}.$$

Now define $C_0 = \mp e^C$ :

$$y = C_0 e^{x^2}.$$

The last step makes the equation nicer, and it's easier to solve for the arbitrary constant when you have an initial value problem.

Remark. Here's a justification for the formal manipulation with $dx$ and $dy$ . Think of x and y as depending on a third variables t, so $x = f(t)$ and $y = g(t)$ . By the Chain Rule,

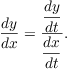
$$\der y x = \dfrac{\der y t}{\der x t}.$$

The initial equation becomes

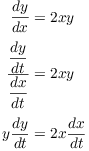
$$\eqalign{ \der y x & = 2 x y \cr \noalign{\vskip2pt} \dfrac{\der y t}{\der x t} & = 2 x y \cr \noalign{\vskip2pt} y \der y t & = 2 x \der x t \cr}$$

Then integrate both sides with respect to t.

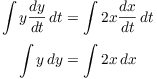
$$\eqalign{ \int y \der y t\,dt & = \int 2 x \der x t\,dt \cr \noalign{\vskip2pt} \int y\,dy & = \int 2x\,dx \cr}$$

Then continue as above. In the example that follows, I'll just work formally with $dx$ and $dy$ .

Example. Solve $\der y x = \dfrac{x}{y} + \dfrac{1}{y}$ , where $y(2) = 4$ .

Separate:

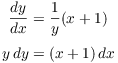
$$\eqalign{ \der y x & = \dfrac{1}{y}(x + 1) \cr \noalign{\vskip2pt} y\,dy & = (x + 1)\,dx \cr}$$

Integrate:

$$\eqalign{ \int y\,dy & = \int (x + 1)\,dx \cr \dfrac{1}{2} y^2 & = \dfrac{1}{2} x^2 + x + C \cr}$$

In this case, solving would produce plus and minus square roots, so I'll leave the equation as is.

Plug in the initial condition: When $x = 2$ , $y = 4$ :

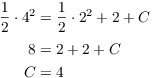
$$\eqalign{ \dfrac{1}{2} \cdot 4^2 & = \dfrac{1}{2} \cdot 2^2 + 2 + C \cr \noalign{\vskip2pt} 8 & = 2 + 2 + C \cr C & = 4 \cr}$$

Hence, the solution is

$$\dfrac{1}{2} y^2 = \dfrac{1}{2} x^2 + x + 4.\quad\halmos$$

I'll use separation of variables to solve the equations for exponential growth and Neton's law of cooling.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga