Substitution

You can use substitution to convert a complicated integral into a simpler one. In these problems, I'll let u equal some convenient x-stuff --- say . To complete the substitution, I must also substitute for . To do this, compute $\der u x = f'(x)$ , so $du = f'(x)\,dx$ . Then $dx = \dfrac{du}{f'(x)}$ .

Example. Compute $\displaystyle \int (2 x + 3)^{100}\,dx$ .

$\int (2 x + 3)^{100}\,dx = \int u^{100} \cdot \dfrac{du}{2} = \dfrac{1}{2} \int u^{100}\,du = \dfrac{1}{202}u ^{101} + C = \dfrac{1}{202} (2 x + 3)^{101} + C.$

$\left[u = 2 x + 3, \quad du = 2\,dx, \quad dx = \dfrac{du}{2}\right] \quad\halmos$

Here's what's going on. By the Chain Rule,

$\der {} x f(g(x)) = f'(g(x)) \cdot g'(x).$

By the definition of antiderivative,

$\int f'(g(x)) \cdot g'(x)\,dx = f(g(x)) + C.$

Now if , I have

$\int f'(u)\,du = f(u) + C = f(g(x)) + C.$

$\int f'(g(x)) \cdot g'(x)\,dx = \int f'(u)\,du.$

The manipulations with and are just a convenient way of doing the substitution. These are not the same " " and " " we used in discussing differentials.

Example. Compute $\displaystyle \int \dfrac{dx}{\sqrt{4 - 7 x}}$ .

$\int \dfrac{dx}{\sqrt{4 - 7 x}} = \int \dfrac{1}{\sqrt{u}}\cdot \left(-\dfrac{du}{7}\right) = -\dfrac{1}{7} \int u^{-1/2}\,du = -\dfrac{2}{7} u^{1/2} + C = -\dfrac{2}{7} (4 - 7 x)^{1/2} + C.$

$\left[u = 4 - 7 x, \quad du = -7\,dx, \quad dx = -\dfrac{du}{7}\right]\quad\halmos$

Example. Later on, I'll derive the integration formula

$\int \dfrac{dx}{x} = \ln |x| + C.$

Use this formula to compute $\displaystyle \int \dfrac{1}{3 x + 1}\,dx$ .

$\int \dfrac{1}{3 x + 1}\,dx = \int \dfrac{1}{u}\cdot \dfrac{du}{3} = \dfrac{1}{3} \int \dfrac{du}{u} = \dfrac{1}{3} \ln |u| + C = \dfrac{1}{3} \ln |3 x + 1| + C.$

$\left[u = 3 x + 1, \quad du = 3\,dx, \quad dx = \dfrac{du}{3}\right] \quad\halmos$

Example. Compute $\displaystyle \int x (x^2 + 5)^{50}\,dx$ .

$\int x(x^2 + 5)^{50}\,dx = \int xu^{50}\cdot \dfrac{du}{2 x} = \dfrac{1}{2} \int u^{50}\,du = \dfrac{1}{102}u^{51} + C = \dfrac{1}{102} (x^2 + 5)^{51} + C.$

$\left[u = x^2 + 5, \quad du = 2 x\,dx, \quad dx = \dfrac{du}{2 x}\right]\quad\halmos$

Notice that in the second step in the last example, the x's cancelled out, leaving only u's. If the x's had failed to cancel, I wouldn't have been able to complete the substitution.

But what made the x's cancel? It was the fact that I got an x from the derivative of . This leads to the following rule of thumb.

$\hbox{Substitute for something whose derivative is also there.}$

Example. Compute $\displaystyle \int (x + 1)\sqrt{x^2 + 2 x + 5}\,dx$ .

$\int (x + 1)\sqrt{x^2 + 2 x + 5}\,dx = \int (x + 1)\sqrt{u}\cdot \dfrac{du}{2(x + 1)} = \dfrac{1}{2} \int \sqrt{u}\,du = \dfrac{1}{2} \cdot \dfrac{2}{3}u^{2/3} + C = \dfrac{1}{3} (x^2 + 2 x + 5)^{3/2} + C.$

$\left[u = x^2 + 2 x + 5, \quad du = (2 x + 2)\,dx = 2(x + 1)\,dx, \quad dx = \dfrac{du}{2(x + 1)}\right]\quad\halmos$

Example. Compute $\displaystyle \int \sin (3 x + 1)\,dx$ .

$\int \sin (3 x + 1)\,dx = \int \sin u\cdot \dfrac{du}{3} = \dfrac{1}{3} \int \sin u\,du = -\dfrac{1}{3} \cos u + C = -\dfrac{1}{3} \cos (3 x + 1) + C.$

$\left[u = 3 x + 1, \quad du = 3\,dx, \quad dx = \dfrac{du}{3}\right] \quad\halmos$

Example. Compute $\displaystyle \int (\sin 5 x)^7 \cos 5 x\,dx$ .

$\int (\sin 5 x)^7 \cos 5 x\,dx = \int u^7 \cos 5 x\cdot \dfrac{du}{5\cos 5 x} = \dfrac{1}{5} \int u^7\,du = \dfrac{1}{40} u^8 + C = \dfrac{1}{40} (\sin 5 x)^8 + C.$

$\left[u = \sin 5 x, \quad du = 5\cos 5 x\,dx, \quad dx = \dfrac{du}{5\cos 5 x}\right]\quad\halmos$

Example. Compute $\displaystyle \int \dfrac{1}{\sqrt{x}(\sqrt{x} + 9)^2}\,dx$ .

$\int \dfrac{1}{\sqrt{x}(\sqrt{x} + 9)^2}\,dx = \int \dfrac{1}{\sqrt{x}u^2}\cdot 2\sqrt{x}\,du = 2 \int u^{-2}\,du = -\dfrac{2}{u} + C = -\dfrac{2}{\sqrt{x} + 9} + C.$

$\left[u = \sqrt{x} + 9, \quad du = \dfrac{dx}{2\sqrt{x}}, \quad dx = 2\sqrt{x}\,du\right]\quad\halmos$

Example. Compute $\displaystyle \int \dfrac{f'(x)}{(f(x) + 3)^2}\,dx$ .

$\int \dfrac{f'(x)}{(f(x) + 3)^2}\,dx = \int \dfrac{f'(x)}{u^2}\cdot \dfrac{du}{f'(x)} = \int \dfrac{du}{u^2} = -\dfrac{1}{u} + C = -\dfrac{1}{f(x) + 3} + C.$

$\left[u = f(x) + 3, \quad du = f'(x)\,dx, \quad dx = \dfrac{du}{f'(x)}\right]\quad\halmos$

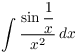Example. Compute $\displaystyle \int \dfrac{\sin \dfrac{1}{x}}{x^2}\,dx$ .

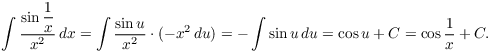
$\int \dfrac{\sin \dfrac{1}{x}}{x^2}\,dx = \int \dfrac{\sin u}{x^2}\cdot (-x^2\,du) = -\int \sin u\,du = \cos u + C = \cos \dfrac{1}{x} + C.$

$\left[u = \dfrac{1}{x}, \quad du = -\dfrac{dx}{x^2}, \quad dx = -x^2\,du\right]\quad\halmos$

The next problem introduces a new idea. In some cases, to replace the x's with u's, you may need to solve the substitution equation for x.

Example. Compute $\displaystyle \int (3 x + 4) (x + 3)^{40}\,dx$ .

There is no valid algebra which will allow me to multiply this out --- unless I plan to multiply out $(x + 3)^{40}$ !

I'll let , so . If I stopped with that, I'd have

$\int (3 x + 4)(x + 3)^{40}\,dx = \int (3 x + 4) u^{40}\,du.$

I can't continue as-is, because I have both x's and u's in the integral.

To get rid of the x's, I solve the substitution equation for x, to get . I can plug this into to get everything in terms of u. Here's the work:

$\int (3 x + 4) (x + 3)^{40}\,dx = \int \left[3 (u - 3) + 4\right] u^{40}\,du = \int (3 u - 5) u^{40}\,du = \int (3 u^{41} - 5 u^{40})\,du =$

$\left[u = x + 3, \quad du = dx, \quad x = u - 3\right]$

$\dfrac{3}{42} u^{42} - \dfrac{5}{41} u^{41} + C = \dfrac{3}{42} (x + 3)^{42} - \dfrac{5}{41} (x + 3)^{41} + C.\quad\halmos$

Example. Compute $\displaystyle \int \dfrac{4 x + 7}{\sqrt{x - 2}}\,dx$ .

In this problem, after making the substitution , I solve the substitution equation for x to get . Then I plug this into to get rid of the x's. Here's the work:

$\int \dfrac{4 x + 7}{\sqrt{x - 2}}\,dx = \int \dfrac{4 (u + 2) + 7}{\sqrt{u}}\,du = \int \dfrac{4 u + 15}{\sqrt{u}}\,du = \int \left(4 \sqrt{u} + \dfrac{15}{\sqrt{u}}\right)\,du =$

$\left[u = x - 2 , \quad du = dx, \quad x = u + 2\right]$

$\dfrac{8}{3} u^{3/2} + 30 u^{1/2} + C = \dfrac{8}{3} (x - 2)^{3/2} + 30 (x - 2)^{1/2} + C.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page