Derivatives of Trigonometric Functions

In this section, I'll discuss limits and derivatives of trig functions. I'll look at an important limit rule first, because I'll use it in computing the derivative of $\sin x$ .

If you graph $y = \sin x$ and $y = x$ , you see that the graphs become almost indistinguishable near $x = 0$ :

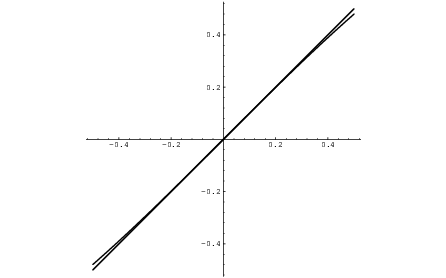
$$\hbox{\epsfysize=2.5in \epsffile{trig-derivatives-1.eps}}$$

That is, as $x \to 0$ , $x \approx \sin x$ . This approximation is often used in applications --- e.g. analyzing the motion of a simple pendulum for small displacements. I'll use it to derive the formulas for differentiating trig functions.

In terms of limits, this approximation says

$$\lim_{x \to 0} \dfrac{\sin x}{x} = 1.$$

(Notice that plugging in $x = 0$ gives $\dfrac{0}{0}$ .) A derivation requires the Squeeze Theorem and a little geometry. What I'll give is not really a proof from first principles; you can think of it as an argument which makes the result plausible.

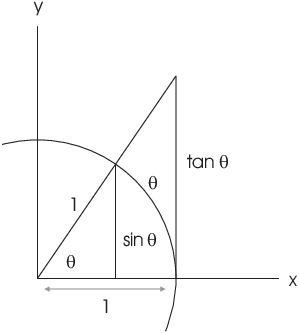
$$\hbox{\epsfysize=3in \epsffile{trig-derivatives-2.eps}}$$

I've drawn a sector subtending an angle $\theta$ inside a circle of radius 1. (I'm using $\theta$ instead of x, since $\theta$ is more often used for the central angle.) The inner right triangle has altitude $\sin \theta$ , while the outer right triangle has altitude $\tan \theta$ . The length of an arc of radius 1 and angle $\theta$ is just $\theta$ .

(I've drawn the picture as if $\theta$ is nonnegative. A similar argument may be given if $\theta < 0$ .)

Clearly,

$$\sin \theta \le \theta \le \tan \theta.$$

Divide through by $\sin \theta$ :

$$1 \le \dfrac{\theta}{\sin \theta} \le \dfrac{1}{\cos \theta}.$$

As $\theta \to 0$ , $\dfrac{1}{\cos \theta} \to 1$ --- just plug in. By the Squeeze Theorem,

$$\lim_{\theta \to 0} \dfrac{\theta}{\sin \theta} = 1.$$

Taking reciprocals, I get

$$\lim_{\theta \to 0} \dfrac{\sin \theta}{\theta} = 1.$$

Example. Compute $\displaystyle \lim_{x \to 0} \dfrac{\sin 7 x}{x}$ .

Plugging in $x = 0$ gives $\dfrac{0}{0}$ . I have to do some more work.

\def\square{\vbox{\hrule\hbox{\vrule height1.5ex\hskip1.5ex\vrule}\hrule}}

The limit formula has the form

$$\lim_{\square \to 0} \dfrac{\sin \square}{\square} = 1.$$

In this example, $\square = 7 x$ . In order to apply the formula, I need $\square = 7 x$ on the bottom of the fraction as well as inside the sine: They must "match". I can't do much about the $7 x$ inside the sine, but I can make a $7 x$ on the bottom easily using algebra:

$$\lim_{x \to 0} \dfrac{\sin 7 x}{x} = 7 \lim_{x \to 0} \dfrac{\sin 7 x}{7 x}.$$

Let $u = 7 x$ . As $x \to 0$ , $u = 7 x \to 0$ . So

$$7 \lim_{x \to 0} \dfrac{\sin 7 x}{7 x} = 7 \lim_{u \to 0} \dfrac{\sin u}{u} = 7 \cdot 1 = 7.$$

I'll often omit writing a substitution like $u = 7 x$ . Once I see that I have something of the form $\dfrac{\sin \square}{\square}$ where $\square \to 0$ , I know it has limit 1.

Example. Compute $\displaystyle \lim_{x \to 0} \dfrac{5 x + \sin 3 x}{\tan 4 x - 7 x \cos 2 x}$ .

Plugging in gives $\dfrac{0}{0}$ .

The idea here is to create terms of the form $\dfrac{\sin \square }{\square}$ , to which I can apply my limit rule. I'll describe the steps I'll take first, then do the computation.

(a) I'll convert the tangent term to sine and cosine. This is because my fundamental rule involves sine, and I also know that $\cos x \to \cos 0 = 1$ as $x \to 0$ (so cosine terms aren't much of an issue).

(b) I'll divide all the terms on the top and the bottom by x. This is in preparation for making terms of the form $\dfrac{\sin \square}{\square}$ .

(c) I'll use the trick I used earlier to fix up numbers so the sine terms all have the form $\dfrac{\sin \square}{\square}$ , where the thing inside the sine and the thing on the bottom match.

Here's the computation:

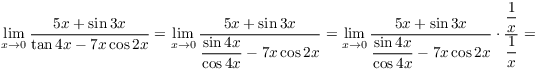
$$\lim_{x \to 0} \dfrac{5 x + \sin 3 x}{\tan 4 x - 7 x \cos 2 x} = \lim_{x \to 0} \dfrac{5 x + \sin 3 x}{\dfrac{\sin 4 x}{\cos 4 x} - 7 x \cos 2 x} = \lim_{x \to 0} \dfrac{5 x + \sin 3 x}{\dfrac{\sin 4 x}{\cos 4 x} - 7 x \cos 2 x} \cdot \dfrac{\dfrac{1}{x}}{\dfrac{1}{x}} =$$

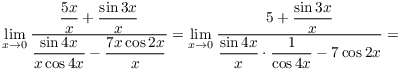
$$\lim_{x \to 0} \dfrac{\dfrac{5 x}{x} + \dfrac{\sin 3 x}{x}}{\dfrac{\sin 4 x}{x \cos 4 x} - \dfrac{7 x \cos 2 x}{x}} = \lim_{x \to 0} \dfrac{5 + \dfrac{\sin 3 x}{x}}{\dfrac{\sin 4 x}{x} \cdot \dfrac{1}{\cos 4 x} - 7 \cos 2 x} =$$

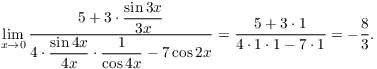
$$\lim_{x \to 0} \dfrac{5 + 3 \cdot \dfrac{\sin 3 x}{3 x}}{4 \cdot \dfrac{\sin 4 x}{4 x} \cdot \dfrac{1}{\cos 4 x} - 7 \cos 2 x} = \dfrac{5 + 3\cdot 1}{4\cdot 1\cdot 1 - 7\cdot 1} = -\dfrac{8}{3}.$$

As $x \to 0$ , the terms $\dfrac{\sin 4 x}{4 x}$ and $\dfrac{\sin 3 x}{3 x}$ both go to 1 by the sine limit formula. On the other hand, the terms $\cos 2 x$ and $\cos 4 x$ both go to 1, since $\cos 0 = 1$ and $\cos x$ is continuous.

Example. (a) Compute $\displaystyle \lim_{x \to 0} \dfrac{1 - \cos x}{x^2}$ .

(b) Compute $\displaystyle \lim_{x \to 0} \dfrac{1 - \cos (x^6)}{x^{12}}$ .

(a) Plugging in gives $\dfrac{0}{0}$ . The limit may or may not exist.

The idea is to use a trig identity $1 - (\cos x)^2 = (\sin x)^2$ to change the cosines into sines, so I can use my sine limit formula. It is kind of like multiplying the top and bottom of a fraction by the conjugate to simplify a radical expression.

$$\lim_{x \to 0} \dfrac{1 - \cos x}{x^2} = \lim_{x \to 0} \dfrac{1 - \cos x}{x^2} \cdot \dfrac{1 + \cos x}{1 + \cos x} = \lim_{x \to 0} \dfrac{1 - (\cos x)^2}{x^2 (1 + \cos x)} = \lim_{x \to 0} \dfrac{(\sin x)^2}{x^2 (1 + \cos x)} =$$

$$\lim_{x \to 0} \left(\dfrac{\sin x}{x}\right)^2 \left(\dfrac{1}{1 + \cos x}\right) = 1^2 \cdot \dfrac{1}{2} = \dfrac{1}{2}.\quad\halmos$$

(b) If you draw the graph near $x = 0$ with a graphing calculator or a computer, you are likely to get unusual results. Here's the picture:

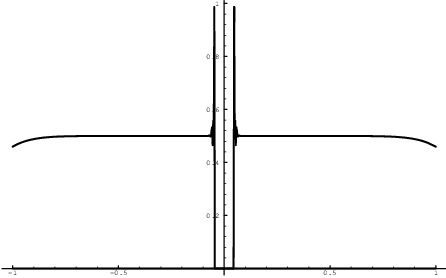
$$\hbox{\epsfysize=2.5in \epsffile{trig-derivatives-3.eps}}$$

The problem is that when x is close to 0, both $x^6$ and $x^{12}$ are very close to 0 --- producing overflow and underflow.

Actually, the limit is easy: Let $y = x^6$ . When $x \to 0$ , $y \to 0$ , so

$$\lim_{x \to 0} \dfrac{1 - \cos (x^6)}{x^{12}} = \lim_{y \to 0} \dfrac{1 - \cos y}{y^2} = \dfrac{1}{2}.$$

For the last step, I used the result from the previous problem.

Example. Compute $\displaystyle \lim_{x \to 0} \dfrac{\tan 7 x}{\tan 2 x}$ .

If you set $x = 0$ , you get $\dfrac{0}{0}$ . Sigh.

I'll see what I can tell from the graph:

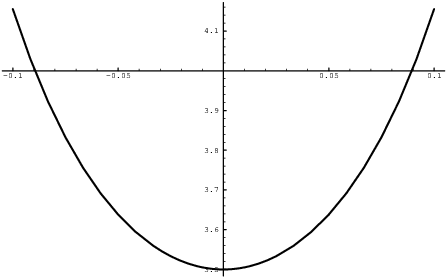
$$\hbox{\epsfysize=2.5in \epsffile{trig-derivatives-4.eps}}$$

It looks as thought the limit is defined, and the picture suggests that it's around 3.5.

First, I'll break the tangents down into sines and cosines:

$$\lim_{x \to 0} \dfrac{\tan 7 x}{\tan 2 x} = \lim_{x \to 0} \dfrac{\sin 7 x}{\cos 7 x}\dfrac{\cos 2 x}{\sin 2 x}.$$

Next, I'll force the $\dfrac{\sin \theta}{\theta}$ form to appear. Since I've got $\sin 7 x$ and $\sin 2 x$ , I need to make a $7 x$ and a $2 x$ to match:

$$\lim_{x \to 0} \dfrac{\sin 7 x}{\cos 7 x}\dfrac{\cos 2 x}{\sin 2 x} = \dfrac{7}{2} \lim_{x \to 0} \dfrac{\sin 7 x}{7 x}\dfrac{2 x}{\sin 2 x} \dfrac{\cos 2 x}{\cos 7 x}.$$

Now take the limit of each piece:

$$\dfrac{\sin 7 x}{7 x} \to 1, \quad \dfrac{2 x}{\sin 2 x} \to 1, \quad \dfrac{\cos 2 x}{\cos 7 x} \to \dfrac{1}{1} = 1.$$

The limit of a product is the product of the limits:

$$\dfrac{7}{2} \lim_{x \to 0} \dfrac{\sin 7 x}{7 x}\dfrac{2 x}{\sin 2 x} \dfrac{\cos 2 x}{\cos 7 x} = \dfrac{7}{2}\cdot 1\cdot 1\cdot 1 = \dfrac{7}{2} = 3.5.\quad\halmos$$

Derivatives of trig functions.

I'll begin with a lemma I'll need to derive the derivative formulas.

Lemma. $\displaystyle \lim_{h \to 0} \dfrac{\cos h - 1}{h} = 0$ .

Proof.

$$\lim_{h \to 0} \dfrac{\cos h - 1}{h} = \lim_{h \to 0} \dfrac{\cos h - 1}{h} \dfrac{\cos h + 1}{\cos h + 1} = \lim_{h \to 0} \dfrac{(\cos h)^2 - 1}{h(\cos h + 1)} = \lim_{h \to 0} -\dfrac{(\sin h)^2}{h(\cos h + 1)} =$$

$$-\left(\lim_{h \to 0} \dfrac{\sin h}{h}\right) \left(\lim_{h \to 0} \dfrac{\sin h}{\cos h + 1}\right) = -1 \cdot \dfrac{0}{1 + 1} = (-1) \cdot 0 = 0.\quad\halmos$$

Proposition.

(a) $\displaystyle \der {} x \sin x = \cos x$ .

(b) $\displaystyle \der {} x \cos x = -\sin x$ .

(c) $\displaystyle \der {} x \tan x = (\sec x)^2$ .

(d) $\displaystyle \der {} x \sec x = \sec x \tan x$ .

(e) $\displaystyle \der {} x \cot x = -(\csc x)^2$ .

(f) $\displaystyle \der {} x \csc x = -\csc x \cot x$ .

Proof. To prove (a), I'll use the sine limit formula

$$\lim_{\theta \to 0} \dfrac{\sin \theta}{\theta} = 1.$$

I'll also need the angle addition formula for sine:

$$\sin (A + B) = \sin A \cos B + \sin B \cos A.$$

Let $f(x) = \sin x$ . Then

$$f'(x) = \lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h} = \lim_{h \to 0} \dfrac{\sin (x + h) - \sin x}{h} = \lim_{h \to 0} \dfrac{\sin x \cos h + \sin h \cos x - \sin x}{h} =$$

$$(\sin x)\cdot \lim_{h \to 0} \dfrac{\cos h - 1}{h} + (\cos x) \lim_{h \to 0} \dfrac{\sin h}{h} = (\sin x)\cdot \lim_{h \to 0} \dfrac{\cos h - 1}{h} + \cos x.$$

The first term goes to 0 by the preceding lemma. Hence,

$$f'(x) = \cos x.$$

That is,

$$\der {} x \sin x = \cos x.$$

To derive the formula for cosine, I'll use the angle addition formula for cosine:

$$\cos (A + B) = \cos A \cos B - \sin A \sin B.$$

Let $f(x) = \cos x$ . Then

$$f'(x) = \lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h} = \lim_{h \to 0} \dfrac{\cos (x + h) - \cos x}{h} = \lim_{h \to 0} \dfrac{\cos x \cos h - \sin x \sin h - \cos x}{h} =$$

$$\lim_{h \to 0} \dfrac{(\cos x \cos h - \cos x) - (\sin x \sin h)}{h} = \lim_{h \to 0} \dfrac{(\cos x)(\cos h - 1) - (\sin x \sin h)}{h} =$$

$$\lim_{h \to 0} (\cos x) \dfrac{\cos h - 1}{h} - (\sin x) \lim_{h \to 0} \dfrac{\sin h}{h} = (\cos x) \cdot 0 - (\sin x) \cdot 1 = -\sin x.$$

I won't do the proofs for the remaining trig functions. The idea is to write

$$\tan x = \dfrac{\sin x}{\cos x}, \quad \cot x = \dfrac{\cos x}{\sin x}, \quad \sec x = \dfrac{1}{\cos x} = (\cos x)^{-1}, \quad \csc x = \dfrac{1}{\sin x} = (\sin x)^{-1}.$$

Then you can use the derivative formulas for sine and cosine together with the quotient rule or the chain rule to compute the derivatives.

As an example, I'll derive the formula for cosecant:

$$\der {} x \csc x = \der {} x \dfrac{1}{\sin x} = -(\sin x)^{-2} \cdot \cos x = -\dfrac{1}{\sin x} \cdot \dfrac{\cos x}{\sin x} = -\csc x \cot x.\quad\halmos$$

Example. Compute the following derivatives.

(a) $\displaystyle \der {} x \left(3 x^3 + \cos x\right)$ .

(b) $\displaystyle \der {} x \left(x \sin x\right)$ .

(c) $\displaystyle \der {} x \dfrac{4 \sin x + 3 x}{5 + 2 \cos x}$ .

(d) $\displaystyle \der {} x (x + \sin x)(x^2 - \tan x)$ .

(e) $\displaystyle \der {} x \dfrac{2 - \sec x}{3 + 4\csc x}$ .

(a)

$$\der {} x \left(3 x^3 + \cos x\right) = 9 x^2 - \sin x.\quad\halmos$$

(b)

$$\der {} x \left(x \sin x\right) = (x)(\cos x) + (\sin x)(1) = x \cos x + \sin x.\quad\halmos$$

(c)

$$\der {} x \dfrac{4 \sin x + 3 x}{5 + 2 \cos x} = \dfrac{(5 + 2\cos x)(4 \cos x + 3) - (4 \sin x + 3 x)(-2 \sin x)}{(5 + 2 \cos x)^2}.\quad\halmos$$

(d)

$$\der {} x (x + \sin x)(x^2 - \tan x) = (x + \sin x)(2 x - (\sec x)^2) + (x^2 - \tan x)(1 - \cos x).\quad\halmos$$

(e)

$$\der {} x \dfrac{2 - \sec x}{3 + 4\csc x} = \dfrac{(3 + 4\csc x)(-\sec x \tan x) - (2 - \sec x)(-4\csc x \cot x)}{(3 + 4\csc x)^2}.\quad\halmos$$

Example. For what values of x does $f(x) = x + \sin x$ have a horizontal tangent?

$$f'(x) = 1 + \cos x.$$

So $f'(x) = 0$ where $\cos x = -1$ . In the range $0 \le x \le 2 \pi$ , this happens at $x = \pi$ . So $f'(x) = 0$ for $x = \pi + 2 n \pi$ , where n is any integer.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga