Alternating Series

If a series has only positive terms, the partial sums get larger and larger. If they get large too rapidly, the series will diverge.

However, if some of the terms are negative, the negative terms may cancel with the positive terms and prevent the partial sums from "blowing up". Here's an example.

This is the harmonic series:

$$\sum_{k = 1}^{\infty} \dfrac{1}{k} = 1 + \dfrac{1}{2} + \dfrac{1}{3} +\dfrac{1}{4} + \cdots.$$

We've seen that it diverges.

This is the alternating harmonic series

$$\sum_{k = 1}^{\infty} (-1)^{k+1} \dfrac{1}{k} = 1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \cdots.$$

The alternating harmonic series converges.

I computed the $1000^{\rm th}$ , $10000^{\rm th}$ , and $100000^{\rm th}$ partial sums of the harmonic series and the alternating harmonic series. Here's what I got:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & & & $s_{1000}$ & & $s_{10000}$ & & $s_{100000}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & harmonic & & 7.48547 & & 9.78761 & & 12.09015 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & alternating harmonic & & 0.69265 & & 0.69310 & & 0.69314 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Of course, this is just numerical evidence, not a proof. However, you can see that while the partial sums of the harmonic series are getting steadily larger, the partial sums for the alternating harmonic series seem to be converging.

The pictures below show the first 20 and the first 100 partial sums of the alternating harmonic series.

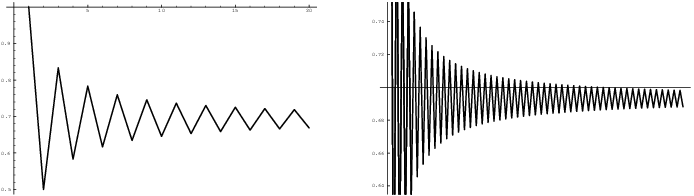
$$\hbox{\epsfysize=1.75in \epsffile{alternating-series-1.eps}} \hskip0.5in \hbox{\epsfysize=1.75in \epsffile{alternating-series-2.eps}}$$

Notice how the partial sums appear to converge by oscillation to a value around 0.69.

A series alternates if the signs of the terms alternate in sign. The Alternating Series Test provides a way of testing an alternating series for convergence.

Theorem. ( Alternating Series Test) Suppose $\displaystyle \sum_{k = 1}^{\infty} (-1)^{k+1} a_k$ is an alternating series (so the $a_k$ 's are positive). Suppose in addition that:

(a) The $a_k$ 's decrease.

(b) $\displaystyle \lim_{k \to \infty} a_k = 0$ .

Then the series $\displaystyle \sum_{k = 1}^{\infty} (-1)^{k+1} a_k$ converges.

It is usually easy to see by inspection that a series alternates. To check that the $a_k$ 's decrease, look at the corresponding function $f(k) = a_k$ . Compute the derivative $f'(k)$ , and use the fact that a function decreases if its derivative is negative.

$\displaystyle \lim_{k \to\infty} a_k$ is the same limit that appears in the Zero Limit Test. By itself, the condition that $\displaystyle \lim_{k \to\infty} a_k = 0$ is not enough to make a series converge. (If the limit isn't 0, the Zero Limit Test says the series diverges.) The Alternating Series Rule augments the computation of this limit with other conditions, and all together these conditions are enough to ensure convergence.

Proof. Consider the alternating series

$$a_1 - a_2 + a_3 - a_4 + \cdots (-1)^{k + 1} a_k + \cdots .$$

The $n^{\rm th}$ partial sum is

$$s_n = a_1 - a_2 + a_3 - a_4 + \cdots (-1)^{n + 1} a_n.$$

The odd partial sums $s_1$ , $s_3$ , $s_5$ decrease:

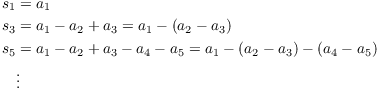
$$\eqalign{ s_1 & = a_1 \cr s_3 & = a_1 - a_2 + a_3 = a_1 - (a_2 - a_3) \cr s_5 & = a_1 - a_2 + a_3 - a_4 - a_5 = a_1 - (a_2 - a_3) - (a_4 - a_5) \cr & \vdots \cr}$$

The reason is that, since the terms of the series decrease, $a_k > a_{k + 1}$ for all k, so $a_k - a_{k + 1} > 0$ for all k. Thus

$$a_2 - a_3 > 0, \quad a_4 - a_5 > 0, \quad a_6 - a_7 > 0, \ldots.$$

So at each step I'm subtracting a sequence of positive numbers from $a_1$ .

Moreover, the odd partial sums are all greater than 0:

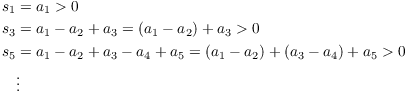
$$\eqalign{ s_1 & = a_1 > 0 \cr s_3 & = a_1 - a_2 + a_3 = (a_1 - a_2) + a_3 > 0 \cr s_5 & = a_1 - a_2 + a_3 - a_4 + a_5 = (a_1 - a_2) + (a_3 - a_4) + a_5 > 0 \cr & \vdots \cr}$$

The terms in parentheses are all positive, because $a_k - a_{k + 1} > 0$ for all k.

Thus, the odd partial sums $s_1$ , $s_3$ , $s_5$ , ... form a decreasing sequence that is bounded below. Therefore, they have a limit:

$$\lim_{n \to \infty} s_{2 n + 1} = L.$$

In similar fashion, the even partial sums $s_2$ , $s_4$ , $s_6$ , ... form an increasing sequence bounded above by $a_1$ . Hence, they have a limit:

$$\lim_{n \to \infty} s_{2 n} = M.$$

But

$$s_{2 n + 1} - s_{2 n} = (a_1 - a_2 + \cdots + a_{2 n} - a_{2 n + 1}) - (a_1 - a_2 + \cdots + a_{2 n}) = a_{2 n + 1}.$$

Then

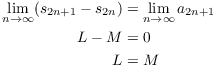
$$\eqalign{ \lim_{n \to \infty} (s_{2 n + 1} - s_{2 n}) & = \lim_{n \to \infty} a_{2 n + 1} \cr L - M & = 0 \cr L & = M \cr}$$

This means that

$$\lim_{n \to \infty} s_{2 n + 1} = \lim_{n \to \infty} s_{2 n}.$$

Their common value is $\displaystyle \lim_{n \to \infty} s_n$ . Since the partial sums approach a limit, the series converges.

Remark. A common mistake is to try to apply the conditions of the Alternating Series Rule, and then, upon discovering that some condition doesn't hold, conclude that the series diverges. The rule only says that if the conditions are true, then the series converges; it does not say what happens if the conditions are not true.

On the other hand, if $\displaystyle \lim_{k \to\infty} a_k \ne 0$ , you can conclude that the series diverges, by the Zero Limit Test.

Example. Apply the Alternating Series Test to the alternating harmonic series $\displaystyle \sum_{k = 1}^{\infty} (-1)^{k+1} \dfrac{1}{k}$ .

The $(-1)^{k+1}$ ensures that the terms alternate.

Let $f(x) = \dfrac{1}{x}$ . Then $f'(x) = -\dfrac{1}{x^2}$ , which is always negative. Since f is always decreasing, the terms of the series decrease in magnitude.

I could also see this by graphing $f(x) = \dfrac{1}{x}$ .

Note that in considering whether the terms decrease, I ignore the $(-1)^{n+1}$ part --- the $\pm 1$ .

Finally,

$$\lim_{n \to \infty} \dfrac{1}{n} = 0.$$

The conditions of the Alternating Series Test hold. Therefore, the series converges.

Example. Does $\displaystyle \sum_{k = 2}^{\infty} (-1)^k \dfrac{k^4}{k^5 + 1}$ converge or diverge?

The series alternates, and

$$\lim_{k \to \infty} \dfrac{k^4}{k^5 + 1} = 0.$$

Set $f(k) = \dfrac{k^4}{k^5 + 1}$ . Then

$$f'(k) = \dfrac{(k^5 + 1)(4 k^3) - (k^4)(5 k^4)}{(k^5 + 1)^2} = \dfrac{4 k^8 + 4 k^3 - 5 k^8}{(k^5 + 1)^2} = \dfrac{4 k^3 - k^8}{(k^5 + 1)^2} = \dfrac{k^3 (4 - k^5)}{(k^5 + 1)^2}.$$

Since $ - k^5 < 0$ for $k \ge 2$ and the other factors in the last expression are positive, I have $f'(k) < 0$ and the terms of the series decrease in absolute value. By the Alternating Series Test, the series converges.

Example. Does $\displaystyle \sum_{n = 0}^{\infty} \dfrac{\cos \pi n}{\sqrt{n + 1}}$ converge or diverge?

This is an alternating series, though it's disguised by the absence of the usual $(-1)^n$ . But note that

$$\cos 0 = 1, \quad \cos \pi = -1, \quad \cos 2 \pi = 1, \quad \cos 3 \pi = -1, \ldots.$$

In fact, $\cos \pi n = (-1)^n$ , so the series can be rewritten as $\displaystyle \sum_{n = 0}^{\infty} \dfrac{(-1)^n}{\sqrt{n + 1}}$ .

The series alternates. If $f(x) = \dfrac{1}{\sqrt{x + 1}}$ , then

$$f'(x) = -\dfrac{1}{2(x + 1)^{3/2}} < 0.$$

Hence, the terms decrease in magnitude.

Finally,

$$\lim_{n \to \infty} \dfrac{1}{\sqrt{n + 1}} = 0.$$

The conditions of the Alternating Series Test are satisfied. Hence, the series converges.

When a series converges, you can approximate the sum to an arbitrary degree of accuracy by adding up sufficiently many terms. How many terms do you need to add up in order to approximate the sum to within a given tolerance? When the series is an alternating series, there's an easy way to find out.

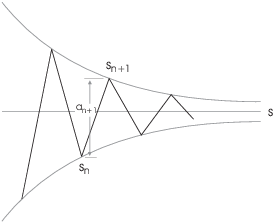
$$\hbox{\epsfysize=2in \epsffile{alternating-series-3.eps}}$$

As the picture shows, the partial sums of an alternating series converge by oscillation to the actual sum. Alternate partial sums are greater than the sum, less than the sum, greater than the sum, and so on.

If $s_n$ is the n-th partial sum (the sum of the terms through the n-th), the error is smaller than the next "jump". The size of the jump from $s_n$ to $s_{n+1}$ is $a_{n+1}$ .

(a) The n-th partial sum of a convergent alternating series is in error by no more than (the absolute value of) the next term in the series.

(b) The actual sum of an alternating series lies between any two consecutive partial sums.

Example. Approximate $\displaystyle \sum_{k = 2}^{\infty} (-1)^k \dfrac{1}{k - \sqrt{k}}$ using the $10^{\rm th}$ and $11^{\rm th}$ partial sums.

I showed in the last example that this alternating series converges. Here's the sum of the first 10 terms.

$$\dfrac{1}{2 - \sqrt{2}} - \dfrac{1}{3 - \sqrt{3}} + \cdots - \dfrac{1}{11 - \sqrt{11}} \approx 1.15141.$$

The next term in the series is $(-1)^{12} \dfrac{1}{12 - \sqrt{12}}$ . Ignoring the sign, this is approximately 0.11715. The estimate 1.15141 is in error by no more than 0.11715, around $10%$ .

In fact, more is true. The last term $\dfrac{1}{11 - \sqrt{11}}$ was subtracted, so the estimate is too small.

The next partial sum is too large:

$$\dfrac{1}{2 - \sqrt{2}} - \dfrac{1}{3 - \sqrt{3}} + \cdots - \dfrac{1}{11 - \sqrt{11}} + \dfrac{1}{12 - \sqrt{12}} \approx 1.26856.$$

The actual sum is between 1.15141 and 1.26856.

Example. (a) Estimate the error if the first 100 terms of the sum $\displaystyle \sum_{k = 1}^\infty \dfrac{(-1)^{k + 1}}{k^2}$ are used to approximate the sum.

(b) How many terms would be required to estimate the sum to within 0.001?

(a) The error in using the $100^{\rm th}$ partial sum is less than the absolute value of the $101^{\rm st}$ term. Hence, the error is less than

$$\dfrac{1}{101^2} = 0.00009 \ldots.\quad\halmos$$

(b) The error in using the $n^{\rm th}$ partial sum $\displaystyle \sum_{k = 1}^n \dfrac{(-1)^{k + 1}}{k^2}$ is less than the absolute value of the $(n + 1)^{\rm st}$ term, which is $\dfrac{1}{(n + 1)^2}$ . So I want

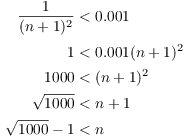
$$\eqalign{ \dfrac{1}{(n + 1)^2} & < 0.001 \cr \noalign{\vskip2pt} 1 & < 0.001 (n + 1)^2 \cr 1000 & < (n + 1)^2 \cr \sqrt{1000} & < n + 1 \cr \sqrt{1000} - 1 & < n \cr}$$

Now $\sqrt{1000} - 1 = 30.62277 \ldots$ . I want the first integer larger than this, and that is $n = 31$ .

Example. Consider the convergent alternating series $\displaystyle \sum_{k = 0}^\infty (-1)^k \dfrac{k^2}{(k + 3)!}$ .

Estimate the smallest value of n so that the partial sum $\displaystyle \sum_{k = 0}^n (-1)^k \dfrac{k^2}{(k + 3)!}$ approximates the actual value of the sum with an error of no more than 0.001.

The partial sum $\displaystyle \sum_{k = 0}^n (-1)^k \dfrac{k^2}{(k + 3)!}$ is in error by no more than the (absolute value of the) next term, which is

$$\dfrac{(n + 1)^2}{((n + 1) + 3)!} = \dfrac{(n + 1)^2}{(n + 4)!}.$$

I want this to be no more than 0.001, so I want the smallest n such that

$$\dfrac{(n + 1)^2}{(n + 4)!} < 0.001.$$

I can't solve this inequality algebraically, so I will use trial and error.

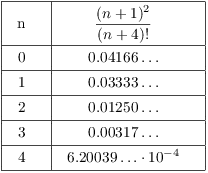
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & n & & $\dfrac{(n + 1)^2}{(n + 4)!}$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 0 & & $0.04166 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 1 & & $0.03333 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 2 & & $0.01250 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 3 & & $0.00317 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 4 & & $6.20039 \ldots \cdot 10^{-4}$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

The first value for which the inequality holds is $n = 4$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga