Arc Length in Polar Coordinates

If a curve is given in polar coordinates $r = f(\theta)$ , an integral for the length of the curve can be derived using the arc length formula for a parametric curve. Regard $\theta$ as the parameter. The parametric arc length formula becomes

$L = \int_a^b \sqrt{\left(\der x \theta\right)^2 + \left(\der y \theta\right)^2}\,d\theta.$

Now $x = r \cos \theta$ and $y = r \sin \theta$ , so

$\der x \theta = -r \sin \theta + \left(\der r \theta\right) \cos \theta,$

$\der y \theta = r \cos \theta + \left(\der r \theta\right) \sin \theta,$

Square and add, using the fact that $(\cos \theta)^2 + (\sin \theta)^2 = 1$ :

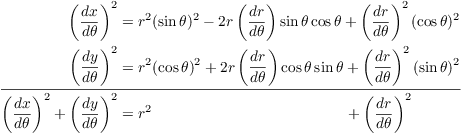
$\eqalign{ \left(\der x \theta\right)^2 & = r^2 (\sin \theta)^2 - 2 r \left(\der r \theta\right) \sin \theta \cos \theta + \left(\der r \theta\right)^2 (\cos \theta)^2 \cr \left(\der y \theta\right)^2 & = r^2 (\cos \theta)^2 + 2 r \left(\der r \theta\right) \cos \theta \sin \theta + \left(\der r \theta\right)^2 (\sin \theta)^2 \cr \noalign{\vskip2pt \hrule \vskip2pt} \left(\der x \theta\right)^2 + \left(\der y \theta\right)^2 & = r^2 \hphantom{\hbox{\hskip1.75in}} + \left(\der r \theta\right)^2 \cr}$

Hence,

$L = \int_a^b \sqrt{r^2 + \left(\der r \theta\right)^2}\,d\theta.$

Note: As with other arc length computations, it's pretty easy to come up with polar curves which lead to integrals with non-elementary antiderivatives. In that case, the best you might be able to do is to approximate the integral using a calculator or a computer.

Example. Find the length of the curve $r = \theta^2 - 1$ from $\theta = 1$ to $\theta = 2$ .

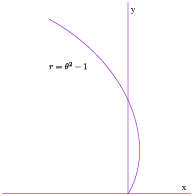
$\hbox{\epsfysize=1.75in \epsffile{arc-length-in-polar1.eps}}$

$\der r \theta = 2 \theta.$

$r^2 + \left(\der r \theta\right)^2 = (\theta^2 - 1)^2 + 4 \theta^2 = \theta^4 - 2 \theta^2 + 1 + 4 \theta^2 = \theta^4 + 2 \theta^2 + 1 = (\theta^2 + 1)^2.$

$\sqrt{r^2 + \left(\der r \theta\right)^2} = \theta^2 + 1.$

The length is

$\int_1^2 (\theta^2 + 1)\,d\theta = \left[\dfrac{1}{3} \theta^3 + \theta\right]_1^2 = \dfrac{10}{3} = 3.33333 \ldots.\quad\halmos$

Example. Find the length of the cardiod $r = 1 + \sin \theta$ for $\theta = 0$ to $\theta = \dfrac{\pi}{2}$ .

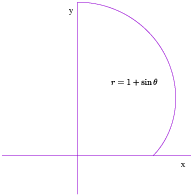
$\hbox{\epsfysize=1.75in \epsffile{arc-length-in-polar2.eps}}$

$\der r \theta = \cos \theta.$

$r^2 + \left(\der r \theta\right)^2 = (1 + \sin \theta)^2 + (\cos \theta)^2 = 1 + 2 \sin \theta + (\sin \theta)^2 + (\cos \theta)^2 = 2 + 2 \sin \theta.$

$\sqrt{r^2 + \left(\der r \theta\right)^2} = \sqrt{2} \sqrt{1 + \sin \theta}.$

I'll do the antiderivative separately:

$\int \sqrt{2} \sqrt{1 + \sin \theta}\,d\theta = \sqrt{2} \int \dfrac{\sqrt{1 + \sin \theta} \sqrt{1 - \sin \theta}}{\sqrt{1 - \sin \theta}}\,d \theta = \sqrt{2} \int \dfrac{\sqrt{1 - (\sin \theta)^2}}{\sqrt{1 - \sin \theta}}\,d \theta =$

$\sqrt{2} \int \dfrac{\sqrt{(\cos \theta)^2}}{\sqrt{1 - \sin \theta}}\,d \theta = \sqrt{2} \int \dfrac{\cos \theta}{\sqrt{1 - \sin \theta}}\,d \theta =$

$\left[u = 1 - \sin \theta, \quad du = -\cos \theta\,d\theta, \quad d\theta = \dfrac{du}{-\cos \theta}\right]$

$\sqrt{2} \int \dfrac{\cos \theta}{\sqrt{u}} \cdot \dfrac{du}{-\cos \theta} = -\sqrt{2} \int \dfrac{1}{\sqrt{u}}\,du = -\sqrt{2} \cdot 2 \sqrt{u} + c = -2 \sqrt{2} \sqrt{1 - \sin \theta} + c.$

The length is

$\int_0^{\pi/2} \sqrt{2} \sqrt{1 + \sin \theta}\,d\theta = \left[-2 \sqrt{2} \sqrt{1 - \sin \theta}\right]_0^{\pi/2} = 2 \sqrt{2} = 2.82842 \ldots.\quad\halmos$

Example. Find the length of the polar curve $r = \left(\sin \dfrac{\theta}{4}\right)^4$ for $\theta = 0$ to $\theta = \pi$ .

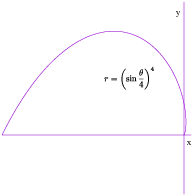
$\hbox{\epsfysize=1.75in \epsffile{arc-length-in-polar3.eps}}$

$\der r \theta = \left(\sin \dfrac{\theta}{4}\right)^3 \cos \dfrac{\theta}{4}.$

$r^2 + \left(\der r \theta\right)^2 = \left(\sin \dfrac{\theta}{4}\right)^8 + \left(\sin \dfrac{\theta}{4}\right)^6 \left(\cos \dfrac{\theta}{4}\right)^2 = \left(\sin \dfrac{\theta}{4}\right)^6 \left[\left(\sin \dfrac{\theta}{4}\right)^2 + \left(\cos \dfrac{\theta}{4}\right)^2\right] = \left(\sin \dfrac{\theta}{4}\right)^6.$

$\sqrt{r^2 + \left(\der r \theta\right)^2} = \left(\sin \dfrac{\theta}{4}\right)^3.$

The length is

$\int_0^\pi \left(\sin \dfrac{\theta}{4}\right)^3\,d\theta.$

I'll do the antiderivative separately:

$\int \left(\sin \dfrac{\theta}{4}\right)^3\,d\theta \int \left(\sin \dfrac{\theta}{4}\right)^2 \sin \dfrac{\theta}{4}\,d\theta = \int \left(1 - \left(\cos \dfrac{\theta}{4}\right)^2\right) \sin \dfrac{\theta}{4}\,d\theta =$

$\left[u = \cos \dfrac{\theta}{4}, \quad du = -\dfrac{1}{4} \sin \dfrac{\theta}{4}\,d\theta, \quad d\theta = -4 \dfrac{du}{\sin \dfrac{\theta}{4}}\right]$

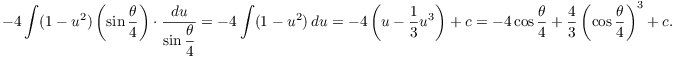
$-4 \int (1 - u^2) \left(\sin \dfrac{\theta}{4}\right) \cdot \dfrac{du}{\sin \dfrac{\theta}{4}} = -4 \int (1 - u^2)\,du = -4 \left(u - \dfrac{1}{3} u^3\right) + c = -4 \cos \dfrac{\theta}{4} + \dfrac{4}{3} \left(\cos \dfrac{\theta}{4}\right)^3 + c.$

$\int_0^\pi \left(\sin \dfrac{\theta}{4}\right)^3\,d\theta = \left[-4 \cos \dfrac{\theta}{4} + \dfrac{4}{3} \left(\cos \dfrac{\theta}{4}\right)^3\right]_0^\pi = \dfrac{8}{3} - \dfrac{5 \sqrt{2}}{3} = 0.30964 \ldots.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page