Suppose a curve is given by continuous functions
![]()
Partition the interval ![]() :
:
![]()
(Note that different partitions may use different numbers of points, as well as different points.)
Consider a subinterval ![]() . The corresponding points
on the curve are
. The corresponding points
on the curve are
![]()
The length of the segment from ![]() to
to ![]() is
is
![]()
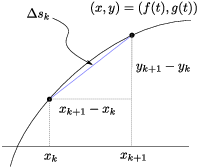
It approximates the length of the curve from ![]() to
to ![]() .
.
For the partition P, the total length of the segments is
![]()
Definition. A curve is
rectifiable if there is a number M such that for every partition
of the interval ![]() ,
,
![]()
If a curve is rectifiable, we can define the
length of the curve as the least upper bound of ![]() taken over all the partitions of the interval.
taken over all the partitions of the interval.
While you can imagine approximating the length of a curve by taking partitions with larger and larger numbers of points, this definition doesn't give a way of computing the exact length.
If the curve is "well-behaved", we can compute the exact
length as follows. Suppose the functions ![]() and
and ![]() are differentiable and have continuous derivatives.
Apply the Mean Value Theorem to f and to g on a typical subinterval
are differentiable and have continuous derivatives.
Apply the Mean Value Theorem to f and to g on a typical subinterval
![]() . Then there are numbers
. Then there are numbers ![]() and
and ![]() such that
such that
![]()
Plugging these into the equation for ![]() above, I get
above, I get
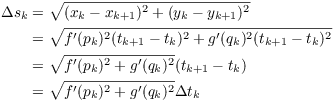
I obtain the sum
![]()
I want to take the limit as the number of subintervals in the
partition becomes infinite (or as the length of the subintervals goes
to 0). There is a technical point here, and that is that I have
two varying quantities ![]() and
and ![]() , so this is not an ordinary Riemann sum. In fact, it's possible to
show (using a result called Bliss's Theorem) that the Riemann sum
produces the expected definite integral:
, so this is not an ordinary Riemann sum. In fact, it's possible to
show (using a result called Bliss's Theorem) that the Riemann sum
produces the expected definite integral:
![]()
This gives the length of the curve. You can also write this in the form
![]()
If the curve is given in the form ![]() , we can think of it as
parametrized by x (so t becomes x). Since
, we can think of it as
parametrized by x (so t becomes x). Since ![]() , the formula
is
, the formula
is
![]()
Likewise, if the curve is given in the form ![]() , the formula is
, the formula is
![]()
Example. Find the length of ![]() for
for ![]() .
.
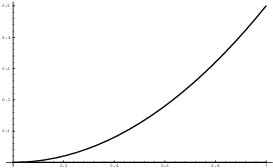
![]()
The length is
![]()
Here's the work for the integral:
![]()
![$$\hfil\raise0.5 in\hbox{$\left[x = \tan \theta, \quad dx = (\sec \theta)^2\,d\theta\right]$} \hskip0.5 in \hbox{\epsfysize=1in \epsffile{arc-length-3.eps}}\hfil$$](arc-length40.png)
![]()
Example. Find the length of the curve
![]()
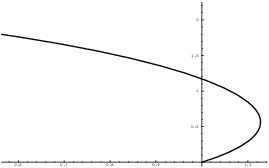
![]()
![]()
![]()
![]()
Hence,
![]()
The length is
![]()
Example. Find the length of ![]() for
for ![]() .
.
![]()
The next step is the algebraic trick in this problem:
![]()
The idea is that I saw when I found ![]() that
that
![]()
Therefore,
![]()
The only difference is in the sign of the ![]() . Since the
first expression is the square of a binomial with a "-",
the second expression must be the square of the same binomial with a
"+".
. Since the
first expression is the square of a binomial with a "-",
the second expression must be the square of the same binomial with a
"+".
Thus,
![]()
The length is
![]()
Copyright 2019 by Bruce Ikenaga