Area in Polar Coordinates

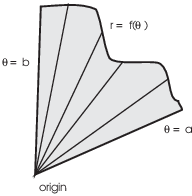
I'll give a heuristic justification for the formula for the area of the region bounded by a polar curve.

As the picture shows, a region in polar is "swept out" as if by a revolving searchlight beam.

$\hbox{\epsfysize=1.75in \epsffile{area-in-polar-coordinates-1.eps}}$

Look at a small wedge-shaped piece of the region. It subtends an angle $d\theta$ and the radius is r.

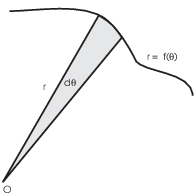
$\hbox{\epsfysize=1.75in \epsffile{area-in-polar-coordinates-2.eps}}$

If $d\theta$ is small, the wedge is approximately a circular wedge.The area of a circular wedge of radius r and angle $d\theta$ is $\dfrac{1}{2}r^2\,d\theta$ , so this is a good approximation to the area of the wedge-shaped piece above.

As usual, I obtain the total area by integrating to add up the areas of the little pieces:

$A = \int_{\theta = a}^{\theta = b} \dfrac{1}{2}r^2\,d\theta.$

In many of these polar area problems, you'll find the double angle formulas useful in doing the integrals:

$(\cos u)^2 = \dfrac{1}{2}(1 + \cos 2 u) \quad\hbox{and}\quad (\sin u)^2 = \dfrac{1}{2}(1 - \cos 2 u).$

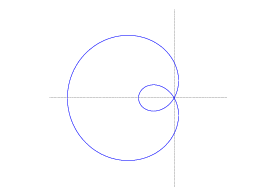
Example. Find the area of the region inside the cardioid $r = 6 + 6 \cos \theta$ .

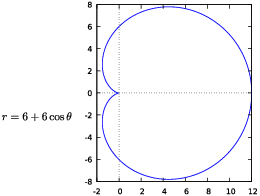
$\hbox{\epsfysize=1.75in \epsffile{area-in-polar-coordinates-3.eps}}$

The entire cardioid is traced out once as $\theta$ goes from 0 to $2 \pi$ . The area is

$\int_0^{2 \pi} \dfrac{1}{2} (6 + 6 \cos \theta)^2\,d\theta = \dfrac{1}{2} \int_0^{2 \pi} \left(36 + 72 \cos \theta + 36 (\cos \theta)^2\right)\,d\theta = \int_0^{2 \pi} \left(18 + 36 \cos \theta + 18 (\cos \theta)^2\right)\,d\theta =$

$\int_0^{2 \pi} \left(18 + 36 \cos \theta + 9 \left(1 + \cos 2 \theta\right)\right)\,d\theta = \left[18 \theta + 36 \sin \theta + 9 \left(\theta + \dfrac{1}{2} \sin 2 \theta\right)\right]_0^{2 \pi} = 54 \pi = 169.64600 \ldots .\quad\halmos$

Example. Find the area of the region inside $r = \cos 2 \theta$ .

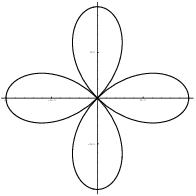
$\hbox{\epsfysize=1.75in \epsffile{area-in-polar-coordinates-4.eps}}$

The 4-leaved rose is traced out once as $\theta$ goes from 0 to $2 \pi$ .

$\int_0^{2 \pi} \dfrac{1}{2} (\cos 2 \theta)^2\,d\theta = \dfrac{1}{2} \int_0^{2 \pi} \dfrac{1}{2} (1 + \cos 4 \theta)\,d\theta = \dfrac{1}{4} \int_0^{2 \pi} \left(1 + \cos 4 \theta\right)\,d\theta =$

$\dfrac{1}{4} \left[\theta + \dfrac{1}{4} \sin 4 \theta\right]_0^{2 \pi} = \dfrac{\pi}{2} = 1.57079 \ldots .$

You could also use symmetry. Note that $\cos 2 \theta = 0$ for $\theta = \pm \dfrac{\pi}{4}$ . Hence, the right-hand leaf is traced out as $\theta$ goes from $-\dfrac{\pi}{4}$ to $\dfrac{\pi}{4}$ , so you could find the area of that leaf and multiply by 4.

Example. Find the area of the region inside the circle $r = \sin \theta$ but outside the cardioid $r = 1 - \cos \theta$ .

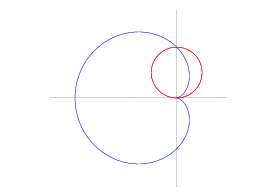
$\hbox{\epsfysize=1.75in \epsffile{area-in-polar-coordinates-5.eps}}$

The region in question is the area inside the circle from 0 to $\dfrac{\pi}{2}$ minus the area inside the cardioid from 0 to $\dfrac{\pi}{2}$ .

$\int_0^{\pi/2} \dfrac{1}{2} \left((\sin \theta)^2 - (1 - \cos \theta)^2\right)\,d\theta.$

I'll simplify the integrand before doing the antiderivative:

$(\sin \theta)^2 - (1 - \cos \theta)^2 = (\sin \theta)^2 - 1 + 2 \cos \theta - (\cos \theta)^2 = -1 + 2 \cos \theta - \cos 2 \theta.$

(I used the identity $\cos 2 \theta = (\cos \theta)^2 - (\sin \theta)^2$ .)

The integral becomes

$\dfrac{1}{2} \int_0^{\pi/2} (-1 + 2 \cos \theta - \cos 2 \theta)\,d\theta = \dfrac{1}{2} \left[-\theta + 2 \sin \theta - \dfrac{1}{2} \sin 2 \theta\right]_0^{\pi/2} = 1 - \dfrac{\pi}{4} = 0.21460 \ldots .\quad\halmos$

Example. Find the area of the region outside $r = \dfrac{1}{2}$ but inside $r = \cos \theta$ .

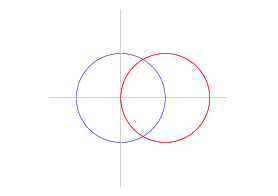
$\hbox{\epsfysize=1.75in \epsffile{area-in-polar-coordinates-6.eps}}$

The curves intersect when $\dfrac{1}{2} = \cos \theta$ . This gives $\theta = \pm \dfrac{\pi}{3}$ . The area is

$\int_{-\pi/3}^{\pi/3} \dfrac{1}{2} \left((\cos \theta)^2 - \dfrac{1}{4}\right)\,d\theta = \dfrac{1}{2} \int_{-\pi/3}^{\pi/3} \left(\dfrac{1}{2} (1 + \cos 2 \theta) - \dfrac{1}{4}\right)\,d\theta = \dfrac{1}{2} \int_{-\pi/3}^{\pi/3} \left(\dfrac{1}{4} + \dfrac{1}{2} \cos 2 \theta\right)\,d\theta =$

$\dfrac{1}{2} \left[\dfrac{1}{4} \theta + \dfrac{1}{4} \sin 2 \theta\right]_{-\pi/3}^{\pi/3} = \dfrac{\sqrt{3}}{8} + \dfrac{\pi}{12} = 0.47830 \ldots .\quad\halmos$

Example. Here is the graph of $r = 1 - 2 \cos \theta$ .

$\hbox{\epsfysize=1.75in \epsffile{area-in-polar-coordinates-7.eps}}$

Label the approximate points on the graph which correspond to $\theta = 0$ , $\theta = \dfrac{\pi}{6}$ , $\theta = \dfrac{\pi}{3}$ , $\theta = \dfrac{\pi}{2}$ , and $\theta = \pi$ . Draw arrows which indicate how the graph is traced out as $\theta$ increases. Then find the area of the region inside the outer loop but outside the inner loop.

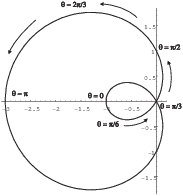
$\hbox{\epsfysize=1.75in \epsffile{area-in-polar-coordinates-8.eps}}$

Notice that the inner loop in the third quadrant is traced out as $\theta$ goes from 0 to $\dfrac{\pi}{3}$ . Why do the points wind up in the third quadrant when the angles are between 0 and $\dfrac{\pi}{3}$ ? Because for those values of $\theta$ the radius r is negative!

You can find the area inside the outer loop and outside the inner loop by subtracting the inner loop area from the outer loop area.

By symmetry, the area of the whole inner loop is twice the area of the bottom part. As we just observed, the bottom part is traced out from 0 to $\dfrac{\pi}{3}$ . So the inner loop area is

$2 \int_0^{\pi/3} \dfrac{1}{2} (1 - 2 \cos \theta)^2\,d\theta = \int_0^{\pi/3} \left(1 - 4 \cos \theta + 4 (\cos \theta)^2\right)\,d\theta.$

Continue with the inner loop area computation:

$\int_0^{\pi/3} \left(1 - 4 \cos \theta + 4 (\cos \theta)^2\right)\,d\theta = \int_0^{\pi/3} \left(1 - 4 \cos \theta + 2 (1 + \cos 2 \theta)\right)\,d\theta =$

$\left[\theta - 4 \sin \theta + 2 \theta + \sin 2 \theta\right]_0^{\pi/3} = \pi - \dfrac{3 \sqrt{3}}{2}.$

As you can see from the picture, the top outer loop is traced out from $\dfrac{\pi}{3}$ to $\pi$ . By symmetry, the area inside the whole outer loop is twice the top outer loop area.

Before I do the computation, let's clear up a common confusion. People often think that in going from $\dfrac{\pi}{3}$ to $\pi$ on the top outer loop, the inner loop stuff is somehow "automagically" subtracted.

Well, it's not so. Think about how the area formula for polar is derived. The area is divided up into thin wedges with their vertices at the origin. The area of a typical wedge is the $\dfrac{1}{2} r^2\, d\theta$ in the area formula.

Look at some wedges for the top outer loop. You can see that they extend from the origin through the inner loop.

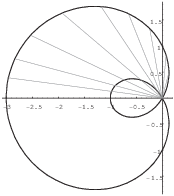
$\hbox{\epsfysize=1.75in \epsffile{area-in-polar-coordinates-9.eps}}$

Thus, when the area formula is applied to the outer loop, it finds the area from the origin all the way out to the outer loop. It doesn't matter that the inner loop is in the way.

With that out of the way, I'll compute the outer loop area. It is

$2 \int_{\pi/3}^\pi \dfrac{1}{2} (1 - 2 \cos \theta)^2\,d\theta = 2 \pi + \dfrac{3 \sqrt{3}}{2}.$

(I'm not writing out the details, since they're essentially the same as those for the inner loop area.)

The area inside the outer loop and outside the inner loop is

$2 \pi + \dfrac{3 \sqrt{3}}{2} - \left(\pi - \dfrac{3 \sqrt{3}}{2}\right) = \pi + 3 \sqrt{3} = 8.33774 \ldots .\quad\halmos$

Example. Find the area of the region which is inside both $r = 2 \sin \theta$ and $r = 2 \sqrt{3} \cos \theta$ simultaneously.

(That is, find the area of the intersection of the interiors of the curves.)

Find where the curves intersect:

$\eqalign{ 2 \sin \theta & = 2 \sqrt{3} \cos \theta \cr \tan \theta & = \sqrt{3} \cr}$

This gives $\theta = \dfrac{\pi}{3}$ .

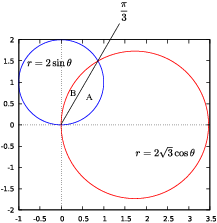
$\hbox{\epsfysize=2in \epsffile{area-in-polar-coordinates-10.eps}}$

The region is shaped like an orange slice, and can be broken up into two pieces. Piece A is the area inside $r = 2 \sin \theta$ (the circle that goes up the y-axis) from $\theta = 0$ to $\theta = \dfrac{\pi}{3}$ . Piece B is the area inside $r = 2 \sqrt{3} \cos \theta$ (the circle that goes along the x-axis) from $\theta = \dfrac{\pi}{3}$ to $\theta = \dfrac{\pi}{2}$ . The area in this example is the sum of the areas of A and B, so it is

$\dfrac{1}{2} \int_0^{\pi/3} (2 \sin \theta)^2\,d\theta + \dfrac{1}{2} \int_{\pi/3}^{\pi/2} (2 \sqrt{3} \cos \theta)^2\,d\theta = 2 \int_0^{\pi/3} (\sin \theta)^2\,d\theta + 6 \int_{\pi/3}^{\pi/2} (\cos \theta)^2\,d\theta =$

$\int_0^{\pi/3} (1 - \cos 2 \theta)\,d\theta + 3 \int_{\pi/3}^{\pi/2} (1 + \cos 2 \theta)\,d\theta = \left[\theta - \dfrac{1}{2} \sin 2 \theta\right]_0^{\pi/3} + \left[\theta + \dfrac{1}{2} \sin 2 \theta\right]_{\pi/3}^{\pi/2} =$

$\dfrac{5 \pi}{6} - \sqrt{3} = 0.88594 \ldots.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page