The Area Between Curves

How do you find the area of a region bounded by two curves? I'll consider two cases.

Suppose the region is bounded above and below by the two curves $f(x)$ and $g(x)$ , and on the sides by $x = a$ and $x = b$ .

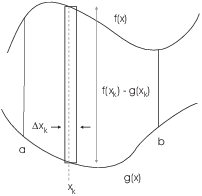
$$\hbox{\epsfysize=1.75in \epsffile{area-1a.eps}}$$

I divide the region up into n vertical rectangles. A typical vertical rectangle (the k-th rectangle is shown in the picture) has thickness $\Delta x_k$ . For instance, if I use n rectangles of equal width, then $\Delta x_k = \dfrac{b - a}{n}$ , and I can just write $\Delta x = \dfrac{b - a}{n}$ , since the widths are all the same. I pick an x-value --- say $x_k$ --- in the base interval of the rectangle. Plugging it into the two functions and subtracting the bottom function from the top, I find that the height of the rectangle is $f(x_k) - g(x_k)$ . Thus, the area of the rectangle is

$$(\hbox{area of rectangle}) = (f(x_k) - g(x_k))\Delta x_k.$$

If I add up (sum) the areas of all the rectangles, I get an approximation to the area between the curves:

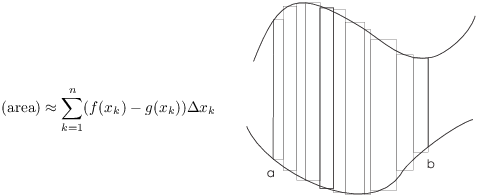
$$\matrix{\displaystyle (\hbox{area}) \approx \sum_{k=1}^n (f(x_k) - g(x_k))\Delta x_k & \vphantom{\hbox{\hskip0.25in}} & \lower0.75in\hbox{\epsfysize=1.75in \epsffile{area-1b.eps}} \cr}$$

To get the exact area, I take the limit as the widths of the rectangles go to 0:

$$(\hbox{area}) = \lim_{\Delta x_k \to 0} \sum_{k=1}^n (f(x_k) - g(x_k))\Delta x_k.$$

Alternatively, if I'm using equal-width rectangles, I can let $n \to \infty$ , where n is the number of rectangles.

The expression on the right is the Riemann sum for $\displaystyle \int_a^b (f(x) - g(x))\,dx$ . Therefore,

$$(\hbox{area}) = \int_a^b (f(x) - g(x))\,dx.$$

It's important to remember that areas are given by Riemann sums. For example, in an application you might need to approximate an area using a finite number of data points. In those cases, you could use the summation approximation given above.

To set up area problems in calculus, I'll use a shortcut rather than writing down the Riemann sums. First, to make the formula reflect the situation, I'll use "top" and "bottom" for the curves, instead of $f(x)$ and $g(x)$ . (This way, you don't need to remember which of f or g is "top" and which is "bottom".)

Now think of dividing the region up into vertical rectangles. The height of the typical rectangle is $(\hbox{top}) - (\hbox{bottom})$ , while the thickness is $dx$ . The area of a typical rectangle is

$$\left((\hbox{top}) - (\hbox{bottom})\right)\,dx.$$

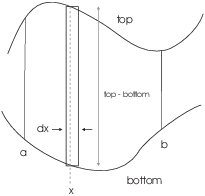
$$\hbox{\epsfysize=1.75in \epsffile{area-1c.eps}}$$

To find the total area, integrate to add up the areas of the little rectangles:

$$A = \int_a^b \left((\hbox{top}) - (\hbox{bottom})\right)\,dx.$$

The $dx$ in the integral is a reminder that I want "top" and "bottom" expressed in terms of x.

The use of "$dx$ " to represent the width of a rectangle is a shortcut for writing $\Delta x$ for the width of a typical rectangle in a subdivision, then summing the rectangle area, then taking a limit to get a Riemann sum and a definite integral. I think this shortcut is harmless, but you should understand what it is a shortcut for!

You can also find areas using horizontal rectangles. I'll skip setting up the Riemann sum and describe the shortcut which is similar to the one for vertical rectangles. Suppose the region is bounded on the sides by two curves ("left" and "right"), and on the top and bottom by $y = c$ and $y = d$ .

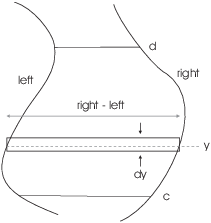
$$\hbox{\epsfysize=2in \epsffile{area-2.eps}}$$

Think of dividing the region up into horizontal rectangles. The height of the typical rectangle is $(\hbox{right}) - (\hbox{left})$ , while the thickness is $dy$ . The area of a typical rectangle is

$$\left((\hbox{right}) - (\hbox{left})\right)\,dy.$$

To find the total area, integrate to add up the areas of the little rectangles:

$$A = \int_c^d \left((\hbox{right}) - (\hbox{left})\right)\,dy.$$

The $dy$ in the integral is a reminder that I want "right" and "left" expressed in terms of y.

In doing problems like the examples below, it's important to draw a picture of the curves (for example, using a computer or a graphing calculator). The picture will help you figure out which curve is the "top curve" and which curve is the "bottom curve". It will also tip you off when the curves intersect.

Example. Find the area of the region bounded above by $y = x^2 + 1$ and below by $y = x - 6$ from $x = -1$ to $x = 3$ .

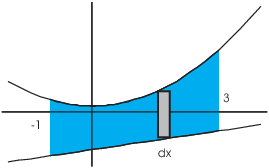
$$\hbox{\epsfysize=1.5in \epsffile{area-3.eps}}$$

The curves don't intersect for $-1 \le x \le 3$ .

I break the region up vertical rectangles. A typical rectangle has thickness $dx$ . $x^2 + 1$ is the top curve and $x - 6$ is the bottom curve.

$$A = \int_{-1}^3 \left((x^2 + 1) - (x - 6)\right)\,dx = \int_{-1}^3 \left(x^2 - x + 7\right)\,dx = \left[\dfrac{1}{3}x^3 - \dfrac{1}{2}x^2 + 7x\right]_{-1}^3 = \dfrac{100}{3}.\quad\halmos$$

Example. Find the area of the region bounded by $y = x^2 - 3x + 12$ and $y = 18 + x - x^2$ .

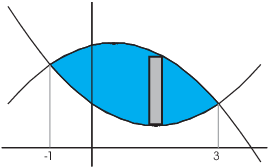
$$\hbox{\epsfysize=1.5in \epsffile{area-4.eps}}$$

Find the intersection points:

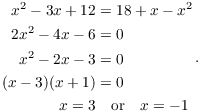
$$\eqalign{ x^2 - 3x + 12 & = 18 + x - x^2 \cr 2 x^2 - 4 x - 6 & = 0 \cr x^2 - 2x - 3 & = 0 \cr (x - 3)(x + 1) & = 0 \cr x = 3 & \quad\hbox{or}\quad x = -1 \cr}.$$

The curves intersect at $x = -1$ and $x = 3$ .

I break the region up vertical rectangles. A typical rectangle has thickness $dx$ . The top curve is $18 + x - x^2$ and the bottom curve is $x^2 - 3x + 12$ .

The area is

$$A = \int_{-1}^3 \left((18 + x - x^2) - (x^2 - 3x + 12)\right)\,dx = \int_{-1}^3 \left(6 + 4x - 2x^2\right)\,dx = \left[6x + 2x^2 - \dfrac{2}{3}x^3\right]_{-1}^3 = \dfrac{64}{3}.\quad\halmos$$

The next example illustrates the importance of drawing a picture before you set up the integral.

Example. Find the area of the region between $y = x + 1$ and $y = 7 - x$ from $x = 2$ to $x = 5$ .

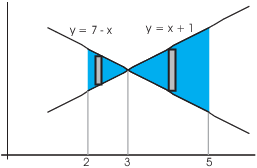
$$\hbox{\epsfysize=1.5in \epsffile{area-5.eps}}$$

The lines appear to cross between $x = 2$ and $x = 5$ . This means that the top curve and bottom curve switch between 2 and 5, and so I will need two integrals.

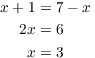
$$\eqalign{ x + 1 & = 7 - x \cr 2 x & = 6 \cr x & = 3 \cr}$$

The lines cross at $x = 3$ , so there are two pieces: One from 2 to 3, and another from 3 to 5. I'll have one integral for each piece; the total area will be the sum of the integrals.

On the left-hand piece, the top curve is $7 - x$ and the bottom curve is $x + 1$ . On the right-hand piece, the top curve is $x + 1$ and the bottom curve is $7 - x$ . The area is

$$A = \int_2^3 \left((7 - x) - (x + 1)\right)\,dx + \int_3^5 \left((x + 1) - (7 - x)\right)\,dx = 5.\quad\halmos$$

You might not have noticed that the lines cross between $x = 2$ and $x = 5$ if you had not drawn the picture!

Example. Find the area of the region bounded above by $y = x + 2$ and by $y = x^2$ , and below by the x-axis, from $x = -2$ to $x = 0$ .

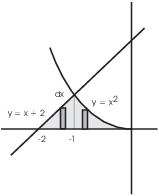
$$\hbox{\epsfysize=1.75in \epsffile{area-6a.eps}}$$

I'll set this problem up in two ways, so that you can compare the computation with vertical rectangles and the computation with horziontal rectangles.

First, I'll set up the area using vertical rectangles.

The top curve is $x + 2$ from $x = -2$ to $x = -1$ , and the top curve is $y = x^2$ from $x = -1$ to $x = 0$ . The bottom curve in each case is $y = 0$ , the x-axis. Therefore, I need two integrals:

$$A = \int_{-2}^{-1} (x + 2)\,dx + \int_{-1}^0 x^2\,dx = \dfrac{5}{6}.$$

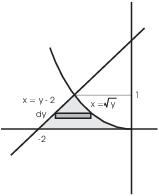
$$\hbox{\epsfysize=1.75in \epsffile{area-6b.eps}}$$

Next, I'll use horizontal rectangles.

The left curve is $x = y - 2$ and the right curve is $x = \sqrt{y}$ . (Notice that I need everything in terms of y, because the thickness of a typical horizontal rectangle is $dy$ .) The area is

$$A = \int_0^1 \left(-\sqrt{y} - (y - 2)\right)\,dy = \dfrac{5}{6}.\quad\halmos$$

In this case, vertical and horizontal rectangles were about the same in terms of the amount of work needed to do the problem. In some problems, however, one approach may be drastically easier than the other.

Example. Find the area of the region bounded by $x = y^2 + 2y$ and $x = y + 20$ .

$$\hbox{\epsfysize=1.75in \epsffile{area-7.eps}}$$

Solve the equations simultaneously:

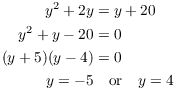
$$\eqalign{ y^2 + 2y & = y + 20 \cr y^2 + y - 20 & = 0 \cr (y + 5)(y - 4) & = 0 \cr y = -5 & \quad\hbox{or}\quad y = 4 \cr}$$

The curves intersect at $y = -5$ and at $y = 4$ .

I'll use horizontal rectangles. The left curve is $x = y^2 + 2y$ and the right curve is $x = y + 20$ . The area is

$$A = \int_{-5}^4 \left((y + 20) - (y^2 + 2y)\right)\,dy = \dfrac{243}{2}.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga