Direct and Limit Comparison

You can often tell that a series converges or diverges by comparing it to a known series. I'll look first at situations where you can establish an inequality between the terms of two series.

Theorem. ( Direct Comparison) Let $\displaystyle \sum_{k = 1}^\infty a_k$ and $\displaystyle \sum_{k = 1}^\infty b_k$ , be series with positive terms.

(a) If $a_k \ge b_k$ for all k and $\displaystyle \sum_{k = 1}^\infty a_k$ converges, then $\displaystyle \sum_{k = 1}^\infty b_k$ converges.

(b) If $a_k \ge b_k$ for all k and $\displaystyle \sum_{k = 1}^\infty b_k$ diverges, then $\displaystyle \sum_{k = 1}^\infty a_k$ diverges.

Proof. Let's look at the proof of (a). I know that $\displaystyle \sum_{k = 1}^\infty a_k$ converges; say $\displaystyle \sum_{k = 1}^\infty a_k = S$ .

The partial sums of $\displaystyle \sum_{k = 1}^\infty a_k$ increase, since the series has positive terms. Therefore, the partial sums are bounded above by S.

Since $a_k \ge b_k$ for all k, the partial sums of $\displaystyle \sum_{k = 1}^\infty a_k$ are greater than or equal to the partial sums of $\displaystyle \sum_{k = 1}^\infty b_k$ :

$a_1 + a_2 + \cdots + a_n \ge b_1 + b_2 + \cdots + b_n.$

Hence, S is an upper bound for the partial sums of $\displaystyle \sum_{k = 1}^\infty b_k$ . Since those partial sums form an increasing sequence that is bounded above, they must have a limit. This means that $\displaystyle \sum_{k = 1}^\infty b_k$ converges.

A similar idea works for (b). In that case, the partial sums are always bigger than the partial sums, but the partial sums go to $\infty$ . Hence, the partial sums go to $\infty$ as well.

In the problems that follow, I'll often have to establish inequalities involving fractions. I need to know how a fraction changes if its top or its bottom is made bigger or smaller. The following table summarizes the ideas:

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & top bigger & & top smaller & & bottom bigger & & bottom smaller & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & fraction becomes \dots & & bigger & & smaller & & smaller & & bigger & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

For example, take the fraction $\dfrac{2}{3}$ . If I change the top from "2" to "3", I make the top bigger. The fraction changes from $\dfrac{2}{3}$ to $\dfrac{3}{3}$ , so the fraction has become bigger. If I change the bottom from "3" to "2", I make the bottom smaller. The fraction changes from $\dfrac{2}{3}$ to $\dfrac{2}{2}$ , so the fraction has become bigger.

Example. Determine whether $\displaystyle \sum_{k = 1}^\infty \dfrac{1}{k^3 + k + 7}$ converges or diverges.

The series has positive terms. In fact, I could use the Integral Test, but who would want to integrate $\dfrac{1}{x^3 + x + 7}$ ?

Instead, note that when k is large, the term should dominate. How does $\dfrac{1}{k^3 + k + 7}$ compare to $\dfrac{1}{k^3}$ ? Well, if you make the bottom smaller, the fraction gets bigger:

$\dfrac{1}{k^3 + k + 7} < \dfrac{1}{k^3}.$

Now $\displaystyle \sum_{k = 1}^\infty \dfrac{1}{k^3}$ is a p-series with , so it converges. Hence, $\displaystyle \sum_{k = 1}^\infty \dfrac{1}{k^3 + k + 7}$ converges by comparison.

Example. Determine whether $\displaystyle \sum_{n = 3}^\infty \dfrac{6 n^2 + 1}{5 n^3 - 2}$ converges or diverges.

When n is large, the term $\dfrac{6 n^2 + 1}{5 n^3 - 2}$ is approximately $\dfrac{6 n^2}{5 n^3} = \dfrac{6}{5} \dfrac{1}{n}$ . This is a term of the harmonic series, which diverges. So I suspect my series diverges.

I have

$\dfrac{6 n^2 + 1}{5 n^3 - 2} > \dfrac{6 n^2}{5 n^3 - 2} > \dfrac{6 n^2}{5 n^3} = \dfrac{6}{5} \dfrac{1}{n}.$

I made the top smaller, then I made the bottom bigger; both cause the fraction to become smaller.

$\displaystyle \sum_{n = 3}^\infty \dfrac{6}{5} \dfrac{1}{n}$ is $\dfrac{6}{5}$ times the harmonic series (minus the and terms), so it diverges. Hence, $\displaystyle \sum_{n = 3}^\infty \dfrac{6 n^2 + 1}{5 n^3 - 2}$ diverges by Direct Comparison.

Example. Determine whether $\displaystyle \sum_{n = 1}^\infty \dfrac{5 \sin n + 11}{6^n + 4}$ converges or diverges.

Since the top is bounded and the bottom is approximately for large n, the series terms "look like" $\dfrac{1}{6^n}$ , which is the general term of a convergent geometric series. So I think my series converges.

I'll use a familiar fact from trigonometry, then do algebra to "build up" the term of my series in the inequality.

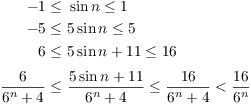
$\eqalign{ -1 \le &\ \sin n \le 1 \cr -5 \le &\ 5 \sin n \le 5 \cr 6 \le &\ 5 \sin n + 11 \le 16 \cr \noalign{\vskip2 pt} \dfrac{6}{6^n + 4} \le &\ \dfrac{5 \sin n + 11}{6^n + 4} \le \dfrac{16}{6^n + 4} < \dfrac{16}{6^n} \cr}$

The series $\displaystyle \sum_{n = 1}^\infty \dfrac{16}{6^n}$ is geometric with ratio $\dfrac{1}{6}$ , so it converges. Hence, the original series converges by direct comparison.

Example. Determine whether $\displaystyle \sum_{k = 1}^\infty \dfrac{\arctan k}{k^3}$ converges or diverges.

The series has positive terms. Since $\arctan k \le \dfrac{\pi}{2}$ ,

$\dfrac{\arctan k}{k^3} \le \dfrac{\pi}{2} \dfrac{1}{k^3}.$

$\displaystyle \sum_{k = 1}^\infty \dfrac{\pi}{2} \dfrac{1}{k^3}$ converges, because it's a p-series with . Therefore, $\displaystyle \sum_{k = 1}^\infty \dfrac{\arctan k}{k^3}$ converges by direct comparison.

Example. Determine whether $\displaystyle \sum_{k = 1}^\infty \dfrac{\sqrt{k + 3}}{k\sqrt{k + 2}}$ converges or diverges.

If you make the top smaller, the fraction gets smaller:

$\dfrac{\sqrt{k + 3}}{k \sqrt{k + 2}} > \dfrac{\sqrt{k + 2}}{k \sqrt{k + 2}} = \dfrac{1}{k}.$

Notice how I avoided changing to k; I changed it to something which cancelled the radical on the bottom.

Now $\displaystyle \sum_{k = 1}^\infty \dfrac{1}{k}$ diverges since it's harmonic. So $\displaystyle \sum_{k = 1}^\infty \dfrac{\sqrt{k + 3}}{k\sqrt{k + 2}}$ diverges, by comparison.

Note that Direct Comparison won't work if the inequalities go the wrong way. For example, consider $\displaystyle \sum_{k = 2}^\infty \dfrac{1}{k^2 - 2}$ . I'd like to compare this to $\displaystyle \sum_{k = 1}^\infty \dfrac{1}{k^2}$ , but if I make the bottom bigger (by adding 2), the fraction gets smaller:

$\dfrac{1}{k^2 - 2} > \dfrac{1}{k^2}.$

It's true that $\displaystyle \sum_{k = 1}^\infty \dfrac{1}{k^2}$ is a convergent p-series ( ), but it's smaller than the given series. I can't draw a conclusion this way.

Nevertheless, $\displaystyle \sum_{k = 1}^\infty \dfrac{1}{k^2}$ is "close to" the given series in some sense. Limit Comparison will make precise the idea that one series is "close to" another, without having to worry about inequalities.

Theorem. ( Limit Comparison) Let $\displaystyle \sum_{k = 1}^\infty a_k$ be a positive term series. Let $\displaystyle \sum_{k = 1}^\infty b_k$ be a positive term series whose behavior is known.

Consider the limiting ratio

$\lim_{k \to \infty} \dfrac{a_k}{b_k}.$

(a) If the limit is a finite positive number, then the two series behave in the same way:

(i) If $\displaystyle \sum_{k = 1}^\infty b_k$ converges, then $\displaystyle \sum_{k = 1}^\infty a_k$ converges.

(ii) If $\displaystyle \sum_{k = 1}^\infty b_k$ diverges, then $\displaystyle \sum_{k = 1}^\infty a_k$ diverges.

(b) If the limit is 0 and $\displaystyle \sum_{k = 1}^\infty b_k$ converges, then $\displaystyle \sum_{k = 1}^\infty a_k$ converges.

(c) If the limit is $+\infty$ and $\displaystyle \sum_{k = 1}^\infty b_k$ diverges, then $\displaystyle \sum_{k = 1}^\infty a_k$ diverges.

The first case is the most important one, and the one I'll usually use. Fortunately, it will work even if you accidentally write $\dfrac{b_k}{a_k}$ instead of $\dfrac{a_k}{b_k}$ . The second and third cases require that you get the fraction "right side up". The phrase "finite positive number" means that in case (a), the limit should not be 0 or $\infty$ .

Proof. I'll sketch a proof in the first part of case (a). Suppose the limit is a finite positive number:

$\lim_{k \to \infty} \dfrac{a_k}{b_k} = L > 0.$

Suppose $\displaystyle \sum_{k = 1}^\infty b_k$ converges. Then there is a number n such that if $k \ge n$ ,

$\dfrac{a_k}{b_k} < L + 1.$

So for $k \ge n$ ,

Apply Direct Comparison to the series $\displaystyle \sum_{k = n}^\infty a_k$ and $\displaystyle \sum_{k = n}^\infty (L + 1) b_k$ . The series $\displaystyle \sum_{k = n}^\infty (L + 1) b_k$ converges, because $\displaystyle \sum_{k = 1}^\infty b_k$ converges. Hence, $\displaystyle \sum_{k = n}^\infty a_k$ converges by Direct Comparison.

Therefore, $\displaystyle \sum_{k = 1}^\infty a_k$ converges as well.

Example. Determine whether $\displaystyle \sum_{k = 1}^\infty \dfrac{4 k^2 + k + 9}{7 k^3 + 13}$ converges or diverges.

The series has positive terms.

When k is large, the top and bottom are dominated by the terms with the biggest powers:

$\dfrac{4 k^2 + k + 9}{7 k^3 + 13} \approx \dfrac{4 k^2}{7 k^3} = \dfrac{4}{7}\cdot \dfrac{1}{k}.$

Compute the limiting ratio:

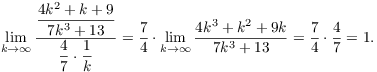
$\lim_{k \to \infty} \dfrac{\dfrac{4 k^2 + k + 9}{7 k^3 + 13}}{\dfrac{4}{7} \cdot \dfrac{1}{k}} = \dfrac{7}{4} \cdot \lim_{k \to \infty} \dfrac{4 k^3 + k^2 + 9 k}{7 k^3 + 13} = \dfrac{7}{4} \cdot \dfrac{4}{7} = 1.$

The limiting ratio is 1, a finite positive number. The series $\displaystyle \sum_{k = 1}^\infty \dfrac{4}{7} \cdot \dfrac{1}{k}$ diverges, because it is harmonic. Hence, the series $\displaystyle \sum_{k = 1}^\infty \dfrac{4 k^2 + k + 9}{7 k^3 + 13}$ diverges by Limit Comparison.

Example. Determine whether $\displaystyle \sum_{k = 2}^\infty \dfrac{4^k + 5}{7^k - 42}$ converges or diverges.

The series has positive terms.

When k is large,

$\dfrac{4^k + 5}{7^k - 42} \approx \dfrac{4^k}{7^k}.$

Compute the limiting ratio:

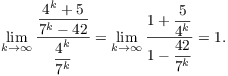
$\lim_{k \to \infty} \dfrac{\dfrac{4^k + 5}{7^k - 42}}{\dfrac{4^k}{7^k}} = \lim_{k \to \infty} \dfrac{1 + \dfrac{5}{4^k}}{1 - \dfrac{42}{7^k}} = 1.$

The limiting ratio is 1, a finite positive number. The series $\displaystyle \sum_{k = 1}^\infty \dfrac{4^k}{7^k}$ is a convergent geometric series (since $\dfrac{4}{7} < 1$ ). Therefore, $\displaystyle \sum_{k = 2}^\infty \dfrac{4^k + 5}{7^k - 42}$ converges, by Limit Comparison.

Contact information

Bruce Ikenaga's Home Page