Improper Integrals

An integral $\displaystyle \int_a^b f(x)\,dx$ is improper if:

1. One of the limits is infinite.

2. The integrand "blows up" somewhere on the interval of integration.

It is possible for both of these things to occur in the same integral.

For example, these integrals are improper because they have infinite limits of integration:

$$\int_0^\infty e^{-3x}\,dx \quad\hbox{and}\quad \int_{-\infty}^\infty \dfrac{x}{x^2 + 9}\,d.$$

These integrals are improper because the integrands become infinite on the intervals of integration:

$$\int_0^4 \dfrac{1}{\sqrt{x}}\,dx \quad\hbox{and}\quad \int_0^2 \dfrac{1}{(x - 1)^2}\,dx.$$

Improper integrals can be reduced to four cases:

1. $\displaystyle \int_a^\infty f(x)\,dx$ .

2. $\displaystyle \int_{-\infty}^b f(x)\,dx$ .

3. $\displaystyle \int_a^b f(x)\,dx$ , where $\displaystyle \lim_{x\to a^+} f(x)$ is undefined.

4. $\displaystyle \int_a^b f(x)\,dx$ , where $\displaystyle \lim_{x\to b^-} f(x)$ is undefined.

You can reduce integrals with more than one "bad thing" going on to the cases above by breaking them up into pieces. For example,

$$\int_{-\infty}^\infty \dfrac{x}{x^2 + 9}\,dx = \int_{-\infty}^0 \dfrac{x}{x^2 + 9}\,dx + \int_0^\infty \dfrac{x}{x^2 + 9}\,dx.$$

The original integral has two infinite limits. I pick a point at random (in this case, 0), and break the integral up there. I now have two improper integrals, each with one infinite limit. They fall into the first two cases above.

Likewise,

$$\int_0^2 \dfrac{1}{(x - 1)^2}\,dx = \int_0^1 \dfrac{1}{(x - 1)^2}\,dx + \int_1^2 \dfrac{1}{(x - 1)^2}\,dx.$$

In the original integral, the function $f(x) = \dfrac{1}{(x - 1)^2}$ blows up in the middle of the interval of integration. I break the integral up at 1, and the two integrals that result fall into the third and fourth cases.

Because I can break more complicated integrals up in these ways, I just have to say what to do in the four cases above.

In the case of an infinite limit, define

$$\int_a^\infty f(x)\,dx = \lim_{b \to \infty} \int_a^b f(x)\,dx,$$

$$\int_{-\infty}^b f(x)\,dx = \lim_{a\to -\infty} \int_a^b f(x)\,dx.$$

If the limit on the right side exists, the integral converges, and the value of the integral is the value of the limit. Otherwise, the integral diverges.

The case where the integrand does not have a limit at one of the endpoints of the integration interval are similar. For example, suppose that $\displaystyle \lim_{x\to a^+} f(x)$ is undefined. Define

$$\int_a^b f(x)\,dx = \lim_{k\to a^+} \int_k^b f(x)\,dx.$$

Likewise, if $\displaystyle \lim_{x\to b^-} f(x)$ is undefined, define

$$\int_a^b f(x)\,dx = \lim_{k\to b^-} \int_a^k f(x)\,dx.$$

As in the infinite case, if the limit on the right side exists, the integral converges, and the value of the integral is the value of the limit. Otherwise, the integral diverges.

Example. Compute $\displaystyle \int_0^\infty e^{-3x}\,dx$ .

Replace the infinite limit with a parameter c, then take the limit as $c \to \infty$ :

$$\int_0^\infty e^{-3x}\,dx = \lim_{c \to \infty} \int_0^c e^{-3x}\,dx = \lim_{c \to \infty} \left[-\dfrac{1}{3} e^{-3x}\right]_0^c = \lim_{c \to \infty} -\dfrac{1}{3}\left(e^{-3c} - 1\right) = -\dfrac{1}{3}\left(0 - 1\right) = \dfrac{1}{3}.$$

The integral represents the area under the graph of $y = e^{-3x}$ from $x = 0$ to $x = \infty$ .

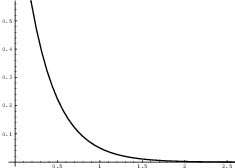
$$\hbox{\epsfysize=1.5in \epsffile{improper-integral-1.eps}}$$

The area is $1/3$ : A region that has infinite extent can have finite area.

Example. Compute $\displaystyle \int_{-\infty}^\infty \dfrac{x}{x^2 + 9}\,dx$ .

When both limits are infinite, divide the integral up into two pieces:

$$\int_{-\infty}^\infty \dfrac{x}{x^2 + 9}\,dx = \int_0^\infty \dfrac{x}{x^2 + 9}\,dx + \int_{-\infty}^0 \dfrac{x}{x^2 + 9}\,dx.$$

The choice of $x = 0$ as the dividing point is arbitrary --- any number will do.

Next, compute each of the integrals. If either integral is undefined, the original integral is undefined. The is true even if one piece approaches $+\infty$ while the other approaches $-\infty$ --- you can't "cancel the infinities".

First,

$$\int_0^\infty \dfrac{x}{x^2 + 9}\,dx = \lim_{a \to +\infty} \int_0^a \dfrac{x}{x^2 + 9}\,dx = \lim_{a \to +\infty} \left[\dfrac{1}{2} \ln (x^2 + 9)\right]_0^a = \dfrac{1}{2} \lim_{a \to +\infty} \left(\ln (a^2 + 9) - \ln 9\right) = +\infty.$$

This is enough to make the original integral undefined --- that is, the integral diverges. I'll compute the second piece anyway:

$$\int_{-\infty}^0 \dfrac{x}{x^2 + 9}\,dx = \lim_{b \to -\infty} \int_b^0 \dfrac{x}{x^2 + 9}\,dx = \lim_{b \to -\infty} \left[\dfrac{1}{2} \ln (x^2 + 9)\right]_b^0 = \dfrac{1}{2} \lim_{b \to -\infty} \left(\ln 9 - \ln (b^2 + 9)\right) = -\infty.$$

I again emphasize that you can't cancel the $+\infty$ from the first piece with the $-\infty$ from the second piece.

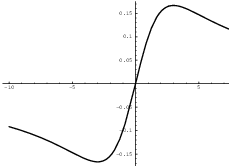
$$\hbox{\epsfysize=1.5in \epsffile{improper-integral-2.eps}}$$

The first integral represents the area under the curve to the right of $x = 0$ . It is positive, and infinite. The second integral represents the (signed) area above the curve to the left of $x = 0$ . Since the curve lies below the x-axis for $x \le 0$ , the integral is negative and infinite.

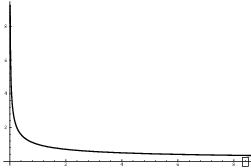
Example. Compute $\displaystyle \int_0^4 \dfrac{1}{\sqrt{x}}\,dx$ .

The integrand $\dfrac{1}{\sqrt{x}}$ is undefined at $x = 0$ , which is the left endpoint of the interval of integration. Replace 0 with a parameter a, and take the (right-hand) limit as $a \to 0$ :

$$\int_0^4 \dfrac{1}{\sqrt{x}}\,dx = \lim_{a \to 0+} \int_a^4 \dfrac{1}{\sqrt{x}}\,dx = \lim_{a \to 0+} \left[2\sqrt{x}\right]_a^4 = \lim_{a \to 0+} \left(4 - 2\sqrt{a}\right) = 4 - 0 = 4.$$

Notice that $y = \dfrac{1}{\sqrt{x}}$ has a vertical asymptote at $x = 0$ :

$$\hbox{\epsfysize=1.5in \epsffile{improper-integral-3.eps}}\quad\halmos$$

Example. Compute $\displaystyle \int_0^2 \dfrac{1}{(x - 1)^2}\,dx$ .

The integrand $\dfrac{1}{(x - 1)^2}$ is defined at $x = 1$ , which lies in the middle of the interval of integration. Break the integral up into two pieces at $x = 1$ , and compute each piece separately. As in the example above, if one piece diverges, the original integral diverges.

$$\int_0^2 \dfrac{1}{(x - 1)^2}\,dx = \int_0^1 \dfrac{1}{(x - 1)^2}\,dx + \int_1^2 \dfrac{1}{(x - 1)^2}\,dx.$$

The first integral is

$$\int_0^1 \dfrac{1}{(x - 1)^2}\,dx = \lim_{a \to 1-} \int_0^a \dfrac{1}{(x - 1)^2}\,dx = \lim_{a \to 1-} \left[-\dfrac{1}{x - 1}\right]_0^a = \lim_{a \to 1-} \left(-\dfrac{1}{a - 1} + 1\right) = +\infty.$$

I could stop here --- the original integral diverges --- but I'll grind out the second integral anyway.

$$\int_1^2 \dfrac{1}{(x - 1)^2}\,dx = \lim_{b \to 1+} \int_b^2 \dfrac{1}{(x - 1)^2}\,dx = \lim_{b \to 1+} \left[-\dfrac{1}{x - 1}\right]_b^2 = \lim_{b \to 1+} \left(-1 + \dfrac{1}{b - 1}\right) = +\infty.$$

Note that (as in the earlier example) if one piece approaches $+\infty$ and the other approaches $-\infty$ , you're not allowed to "cancel the infinities".

Example. Compute $\displaystyle \int_0^\infty \dfrac{1}{(x - 5)^{1/3}}\,dx$ .

This integral is improper for two reasons: First, the integrand $f(x) = \dfrac{1}{(x - 5)^{1/3}}$ is undefined at $x = 5$ , which is in the interval of integration. Second, one of the limits of integration is infinite.

First, I need to break the integral up into two pieces at $x = 5$ :

$$\int_0^\infty \dfrac{1}{(x - 5)^{1/3}}\,dx = \int_0^5 \dfrac{1}{(x - 5)^{1/3}}\,dx + \int_5^\infty \dfrac{1}{(x - 5)^{1/3}}\,dx.$$

In the second integral, the lower limit $x = 5$ makes the integrand undefined and the upper limit is infinite. Thus, I need to break the second integral up into two pieces. I can choose any point between 5 and $\infty$ as the break point; I'll use $x = 6$ .

$$\int_0^5 \dfrac{1}{(x - 5)^{1/3}}\,dx + \int_5^\infty \dfrac{1}{(x - 5)^{1/3}}\,dx = \int_0^5 \dfrac{1}{(x - 5)^{1/3}}\,dx + \int_5^6 \dfrac{1}{(x - 5)^{1/3}}\,dx \int_6^\infty \dfrac{1}{(x - 5)^{1/3}}\,dx.$$

Next, I'll compute the three integrals. Note that

$$\int \dfrac{1}{(x - 5)^{1/3}}\,dx = \dfrac{3}{2}(x - 5)^{2/3} + C.$$

(Let $u = x - 5$ .)

First,

$$\int_0^5 \dfrac{1}{(x - 5)^{1/3}}\,dx = \lim_{a\to 5^-} \int_0^a \dfrac{1}{(x - 5)^{1/3}}\,dx = \lim_{a\to 5^-} \left[\dfrac{3}{2}(x - 5)^{2/3}\right]_0^a = \lim_{a\to 5^-} \left(\dfrac{3}{2}(a - 5)^{2/3} - \dfrac{3}{2}(-5)^{2/3}\right) =$$

$$0 - \dfrac{3}{2}(-5)^{2/3} = -\dfrac{3}{2}5^{2/3}.$$

(Note that $(-5)^{2/3} = 5^{2/3}$ since the even power "2" eliminates the minus sign.)

Next,

$$\int_5^6 \dfrac{1}{(x - 5)^{1/3}}\,dx = \lim_{b \to 5^+} \int_b^6 \dfrac{1}{(x - 5)^{1/3}}\,dx = \lim_{b \to 5^+} \left[\dfrac{3}{2}(x - 5)^{2/3}\right]_b^6 = \lim_{b \to 5^+} \left(\dfrac{3}{2} - \dfrac{3}{2}(b - 5)^{2/3}\right) = \dfrac{3}{2} - 0 = \dfrac{3}{2}.$$

Finally,

$$\int_6^\infty \dfrac{1}{(x - 5)^{1/3}}\,dx = \lim_{c\to \infty} \int_6^c \dfrac{1}{(x - 5)^{1/3}}\,dx = \lim_{c\to \infty} \left[\dfrac{3}{2}(x - 5)^{2/3}\right]_6^c = \lim_{c\to \infty} \left(\dfrac{3}{2}(c - 5)^{2/3} - \dfrac{3}{2}\right) =$$

$$\infty - \dfrac{3}{2} = \infty.$$

The first two integrals converged, but the third diverged to $\infty$ . Therefore,

$$\int_0^\infty \dfrac{1}{(x - 5)^{1/3}}\,dx = \infty.\quad\halmos$$

In some cases, you can tell whether an improper integral converges or diverges by comparing it to another integral.

1. If $f(x) \ge g(x) \ge 0$ and $\displaystyle \int_a^\infty f(x)\,dx$ converges, then $\displaystyle \int_a^\infty g(x)\,dx$ converges.

2. If $g(x) \ge f(x) \ge 0$ and $\displaystyle \int_a^\infty f(x)\,dx\to \infty$ , then $\displaystyle \int_a^\infty g(x)\,dx \to \infty$ .

Similar results hold for improper integrals where the integrand blows up on the interval of integration.

Example. Show that $\displaystyle \int_1^\infty e^{-x^2}\,dx$ converges.

The antiderivative $\displaystyle \int e^{-x^2}\,dx$ can't be computed in closed form. Instead, I'll compare this integral to an integral which I can show converges.

Since the limits of integration are 1 to $\infty$ , $x \ge 1$ , and therefore $e^{-x^2} \le xe^{-x^2}$ .

$$\hbox{\epsfysize=1.75in \epsffile{improper-integral-4.eps}}$$

So

$$\int_1^\infty e^{-x^2}\,dx \le \int_1^\infty x e^{-x^2}\,dx = \lim_{b \to \infty} \int_1^b x e^{-x^2}\,dx = \lim_{b \to \infty} \left[-\dfrac{1}{2} e^{-x^2}\right]_1^b = \lim_{b \to \infty} \left(\dfrac{1}{2} e^{-1} - \dfrac{1}{2} e^{-b^2}\right) = \dfrac{1}{2} e^{-1}.$$

(I did the integral using the substitution $u = -x^2$ .) $\displaystyle \int_1^\infty xe^{-x^2}\,dx$ converges, and it is larger than the original integral. Therefore, $\displaystyle \int_1^\infty e^{-x^2}\,dx$ converges.

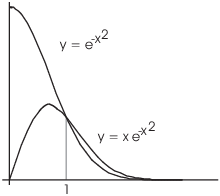
You can see why this works geometrically by considering the picture above. $\displaystyle \int_1^\infty xe^{-x^2}\,dx$ represents the area under $y = xe^{-x^2}$ from 1 to $\infty$ . The computation I did shows that this area is finite --- in fact, it's $\dfrac{1}{2}e^{-1}$ .

$\displaystyle \int_1^\infty e^{-x^2}\,dx$ represents the area under $y = e^{-x^2}$ from 1 to $\infty$ . This area is less than the area under $y = xe^{-x^2}$ . Since the area under $y = xe^{-x^2}$ is finite, the area under $y = e^{-x^2}$ must be finite as well.

Example. Does the following integral converge or diverge?

$$\int_1^2 \dfrac{e^x}{x - 1}\,dx.$$

Note that $f(x) = \dfrac{e^x}{x - 1}$ is positive for $1 < x \le 2$ . Also, $f(1)$ is undefined.

For $1 \le x \le 2$ , I have $e^x \ge e^1 = e > 1$ (because $e = 2.71828182845 \ldots$ ). So

$$\dfrac{e^x}{x - 1} > \dfrac{1}{x - 1}.$$

Hence,

$$\int_1^2 \dfrac{e^x}{x - 1}\,dx > \int_1^2 \dfrac{1}{x - 1}\,dx.$$

Now do the second integral:

$$\int_1^2 \dfrac{1}{x - 1}\,dx = \lim_{b \to 1^+} \int_b^2 \dfrac{1}{x - 1}\,dx = \lim_{b \to 1^+} \left[\ln |x - 1|\right]_b^2 = \lim_{b \to 1^+} \left(\ln 1 - \ln |b - 1|\right) = +\infty.$$

Therefore, $\displaystyle \int_1^2 \dfrac{e^x}{x - 1}\,dx$ diverges by comparison.

Here's the graph of the two functions:

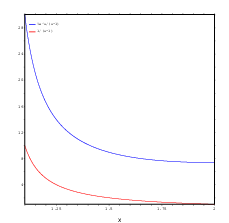
$$\hbox{\epsfysize=2in \epsffile{improper-integral-5.eps}}$$

The upper graph is $y = \dfrac{e^x}{x - 1}$ and the lower graph is $y = \dfrac{1}{x - 1}$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga