The Integral Test

The Integral Test tests a series for comvergence or divergence by comparing it to an integral constructing from the series terms.

Theorem. ( Integral Test) Suppose $\displaystyle \sum_{k = 1}^\infty a_k$ is a series in which the terms are positive. Let $f(x)$ be the function you get by replacing k by x in $a_k$ . Suppose that:

(i) f is continuous for $x \ge 1$ .

(ii) f decreases for $x \ge 1$ .

Then:

(a) If $\displaystyle \int_1^\infty f(x)\,dx$ converges, so does $\displaystyle \sum_{k = 1}^\infty a_k$ .

(b) If $\displaystyle \int_1^\infty f(x)\,dx$ diverges, so does $\displaystyle \sum_{k = 1}^\infty a_k$ .

Proof. Divide the interval $[1, n + 1]$ up into rectangles of width 1, using the left-hand endpoints to get the heights. The function f decreases, so the picture looks like this:

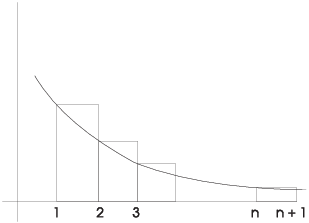
$$\hbox{\epsfysize=2in \epsffile{integral-test-1.eps}}$$

The sum of the rectangle areas is the $n^{\rm th}$ partial sum, and it is clearly bigger than the area under the curve:

$$s_n = f(1) + f(2) + \cdots + f(n) > \int_1^{n+1} f(x)\,dx.$$

Therefore, if $\displaystyle \lim_{n \to \infty} \int_1^{n+1} f(x)\,dx$ diverges, so does $\displaystyle \lim_{n \to \infty} s_n$ , but $\displaystyle \lim_{n \to \infty} s_n$ is the sum of the series.

Next, divide the interval $[1, n]$ up into rectangles of width 1, but use the right-hand endpoints to get the heights. The picture looks like this:

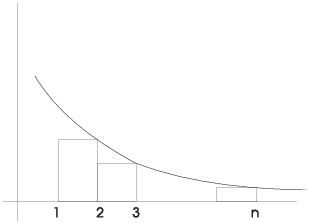
$$\hbox{\epsfysize=2in \epsffile{integral-test-2.eps}}$$

The sum of the rectangle areas is clearly smaller than the area under the curve:

$$f(2) + f(3) + \cdots + f(n) < \int_1^n f(x)\,dx.$$

If I add $f(1)$ to both sides, the left side becomes the n-th partial sum:

$$s_n = f(1) + f(2) + f(3) + \cdots + f(n) < f(1) + \int_1^n f(x)\,dx.$$

If $\displaystyle \lim_{n \to \infty} \int_1^n f(x)\,dx$ converges, then the partial sums $s_n$ form an increasing sequence that is bounded above by the integral. Hence, $\displaystyle \sum_{k = 1}^\infty a_k$ converges.

As an application, I'll prove the convergence criteria for p-series.

Proposition. The p-series $\displaystyle \sum_{n = 1}^\infty \dfrac{1}{n^p}$ converges if $p > 1$ and diverges if $0 < p \le 1$ .

Proof. The series $\displaystyle \sum_{n = 1}^\infty \dfrac{1}{n^p}$ has positive terms, and $f(x) = \dfrac{1}{x^p}$ is continuous for $x \ge 1$ .

Suppose $p > 1$ . Then

$$\int_1^\infty \dfrac{1}{x^p}\,dx = \lim_{b \to \infty} \int_1^b \dfrac{1}{x^p}\,dx = \lim_{b \to \infty} \left[-\dfrac{1}{p - 1} \dfrac{1}{x^{p - 1}}\right]_1^b = \lim_{b \to \infty} \left(-\dfrac{1}{p - 1} \dfrac{1}{b^{p - 1}} + \dfrac{1}{p - 1}\right).$$

Note that $p > 1$ implies $p - 1 > 0$ . Thus, in the term $\dfrac{1}{b^{p - 1}}$ there is a positive power of b on the bottom. Hence, $\displaystyle \lim_{b \to \infty} \dfrac{1}{b^{p - 1}} = 0$ . That is,

$$\int_1^\infty \dfrac{1}{x^p}\,dx = \dfrac{1}{p - 1}.$$

Since the integral converges, the series converges by the Integral Test. A similar argument shows that if $0 < p \le 1$ , then the series diverges.

Example. Determine whether the series $\displaystyle \sum_{k = 1}^\infty k e^{-k}$ converges or diverges.

$x e^{-x}$ is something you can integrate, so it's natural to try the Integral Test. (And if the general term of the series is something that would be difficult to integrate, you should try a different test!)

For $k \ge 1$ , $k e^{-k} > 0$ . The series has positive terms.

Let $f(x) = x e^{-x}$ . f is continuous for $x \ge 1$ . Note that

$$f'(x) = (1 - x)e^{-x} < 0 \quad\hbox{for}\quad x > 1.$$

Hence, f decreases for $x \ge 1$ . The hypotheses of the Integral Test are satisfied. (It's important to check the hypothesis before applying the test!)

Compute the improper integral:

$$\int_1^\infty x e^{-x}\,dx = \lim_{c \to \infty} \int_1^c x e^{-x}\,dx = \lim_{c \to \infty} \left[-x e^{-x} - e^{-x}\right]_1^c =$$

$$\lim_{c \to \infty} \left(-c e^{-c} - e^{-c} + e^{-1} + e^{-1}\right) = 2 e^{-1}.$$

Here's the parts table:

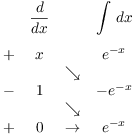
$$\matrix{& \der {} x & & \displaystyle \int\,dx \cr & & & \cr + & x & & e^{-x} \cr & & \searrow & \cr - & 1 & & -e^{-x} \cr & & \searrow & \cr + & 0 & \rightarrow & e^{-x} \cr}$$

Since the integral converges, the series converges by the Integral Test.

Example. Determine whether the series $\displaystyle \sum_{k = 1}^\infty \dfrac{k^2}{k^3 + 2}$ converges or diverges.

The series has positive terms, and $f(x) = \dfrac{x^2}{x^3 + 2}$ is continuous for $x \ge 1$ . Compute the derivative:

$$f'(x) = \dfrac{(x^3 + 2)(2 x) - (x^2)(3 x^2)}{(x^3 + 2)^2} = \dfrac{4 x - x^4}{(x^3 + 2)^2} = \dfrac{x(4 - x^3)}{(x^3 + 2)^2}.$$

Notice that $f'(x) > 0$ for $x = 1$ . In fact, the first two terms of the series are $\dfrac{1}{3}$ and $\dfrac{2}{5}$ , so the terms actually increase at the start.

However, $f'(x) < 0$ for $x \ge 2$ , so the terms eventually decrease. Thus, the Integral Test applies to $\displaystyle \sum_{k = 2}^\infty \dfrac{k^2}{k^3 + 2}$ (the original series with the first term removed). Since the two series only differ by one term, if one converges, the other converges, and if one diverges, the other diverges.

Therefore, there's actually no harm in applying the Integral Test to the original series, even though, strictly speaking, it doesn't have decreasing terms: Eventually decreasing is good enough.

Comput the integral:

$$\int_1^\infty \dfrac{x^2}{x^3 + 2}\,dx = \lim_{b \to \infty} \int_1^b \dfrac{x^2}{x^3 + 2}\,dx = \lim_{b \to \infty} \int_3^{b^3 + 2} \dfrac{x^2}{u} \cdot \dfrac{du}{3 x^2} = \dfrac{1}{3} \lim_{b \to \infty} \int_3^{b^3 + 2} \dfrac{du}{u} =$$

$$\left[u = x^3 + 2, \quad du = 3 x^2\,dx, \quad dx = \dfrac{du}{3 x^2}; \quad x = 1, \quad u = 3; \quad x = b, \quad u = b^3 + 2\right]$$

$$\dfrac{1}{3} \lim_{b \to \infty} \left[\ln |u|\right]_3^{b^3 + 2} = \dfrac{1}{3} \lim_{b \to \infty} \left(\ln |b^3 + 2| - \ln 3\right) = \infty.$$

Since the integral diverges, the series diverges, by the Integral Test.

Warning: The value of the integral in the Integral Test is not equal to the sum of the series.

The proof of the Integral Test yields the formula

$$f(1) + \int_1^n f(x)\,dx > s_n > \int_1^{n+1} f(x)\,dx.$$

You can use this to estimate the partial sums of a series to which the Integral Test applies.

Example. Estimate the sum of the first 1000 terms of

$$\sum_{k = 1}^\infty \dfrac{1}{{\root 3 \of k}}.$$

This is a divergent p-series with $p = \dfrac{1}{3}$ , so the Integral Test applies. I have

$$f(1) + \int_1^{1000} \dfrac{1}{x^{1/3}}\,dx > s_{1000} > \int_1^{1001} \dfrac{1}{x^{1/3}}\,dx.$$

You can compute the integrals for yourself; you'd get

$$f(1) + \int_1^{1000} =149.5 \quad\hbox{and}\quad \int_1^{1001} \dfrac{1}{x^{1/3}}\,dx \approx 148.59998.$$

Hence, $148.59998 < s_{1000} < 149.5$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga