Integration Review

In this section, I'll review some of our integration techniques.

Example. Compute $\displaystyle \int \ln (1 + x^2)\,dx$ .

Use integration by parts:

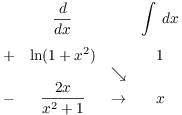
$$\matrix{& \der {} x & & \displaystyle \int\,dx \cr & & & \cr + & \ln (1 + x^2) & & 1 \cr & & \searrow & \cr - & \dfrac{2 x}{x^2 + 1} & \to & x \cr}$$

$$\int \ln (1 + x^2)\,dx = x \ln (1 + x^2) - 2 \int \dfrac{x^2}{x^2 + 1}\,dx = x \ln (1 + x^2) - 2\int \left(1 - \dfrac{1}{x^2 + 1}\right)\,dx =$$

$$x \ln (1 + x^2) - 2 x + 2 \tan^{-1} x + C.\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{7 x^3 - 2 x^2 + 12 - 8}{x^2(x^2 + 4)}\,dx$ .

Use partial fractions:

$$\dfrac{7 x^3 - 2 x^2 + 12 - 8}{x^2(x^2 + 4)} = \dfrac{a x + b}{x^2 + 4} + \dfrac{c}{x} + \dfrac{d}{x^2},$$

$$7 x^3 - 2 x^2 + 12 x - 8 = (a x + b)x^2 + c x(x^2 + 4) + d(x^2 + 4).$$

Let $x = 0$ . Then $-8 = 4 d$ , so $d = -2$ . Therefore,

$$7 x^3 - 2 x^2 + 12 x - 8 = (a x + b)x^2 + c x(x^2 + 4) - 2(x^2 + 4).$$

Differentiate:

$$21 x^2 - 4 x + 12 = (a x + b)(2 x) + a x^2 + c x(2 x) + c(x^2 + 4) - 4 x.$$

Let $x = 0$ . Then $12 = 4 c$ , so $c = 3$ . Therefore,

$$21 x^2 - 4 x + 12 = (a x + b)(2 x) + a x^2 + 3 x(2 x) + 3(x^2 + 4) - 4 x,$$

$$21 x^2 - 4 x + 12 = (a x + b)(2 x) + a x^2 + 6 x^2 + 3(x^2 + 4) - 4 x.$$

Differentiate:

$$42 x - 4 = (a x + b)(2) + a(2 x) + a(2 x) + 12 x + 6 x - 4.$$

Let $x = 0$ . Then $-4 = 2 b - 4$ , so $b = 0$ . Therefore,

$$42 x - 4 = (a x)(2) + a(2 x) + a(2 x) + 12 x + 6 x - 4.$$

Let $x = 1$ . Then $38 = 6 a + 14$ , so $a = 4$ .

Therefore,

$$ \int \dfrac{7 x^3 - 2 x^2 + 12 - 8}{x^2(x^2 + 4)}\,dx = \int \left(\dfrac{4 x}{x^2 + 4} + \dfrac{3}{x} - \dfrac{2}{x^2}\right)\,dx = 2 \ln |x^2 + 4| + 3\ln |x| + \dfrac{2}{x} + C.\quad\halmos$$

Example. Compute $\displaystyle \int (\cos 3 x)^4\,dx$ .

I'll use the double angle formula

$$(\cos \theta)^2 = \dfrac{1}{2} (1 + \cos 2 \theta).$$

Begin by writing the fourth power as the square of a square, then use the formula:

$$\int (\cos 3 x)^4\,dx = \int \left((\cos 3 x)^2\right)^2\,dx = \int \left(\dfrac{1}{2}(1 + \cos 6 x)\right)^2\,dx = \dfrac{1}{4} \int \left(1 + 2 \cos 6 x + (\cos 6 x)^2\right)\,dx =$$

$$\dfrac{1}{4} \int \left(1 + 2 \cos 6 x + \dfrac{1}{2}(1 + \cos 12 x)\right)\,dx = \dfrac{1}{4} \int \left(\dfrac{3}{2} + 2\cos 6 x + \dfrac{1}{2} \cos 12 x\right)\,dx =$$

$$\dfrac{3}{8} x + \dfrac{1}{12} \sin 6 x + \dfrac{1}{96} \sin 12 x + C.\quad\halmos$$

Example. Compute $\displaystyle \int (\cos 3 x)^4 (\sin 3 x)^3\,dx$ .

Since one of the powers of sine or cosine is odd, I do not use a double angle formula.

$$\int (\cos 3 x)^4(\sin 3 x)^3\,dx = \int (\cos 3 x)^4(\sin 3 x)^2(\sin 3 x\,dx) = \int (\cos 3 x)^4\left(1 - (\cos 3 x)^2\right)(\sin 3 x\,dx) =$$

$$\left[u = \cos 3 x, \quad du = -3 \sin 3 x\,dx, \quad dx = \dfrac{du}{-3 \sin 3 x}\right]$$

$$\int u^4(1 - u^2)(\sin 3 x)\left(\dfrac{du}{-3 \sin 3 x}\right) = \dfrac{1}{3} \int (u^6 - u^4)\,du = \dfrac{1}{3} \left(\dfrac{1}{7}u^7 - \dfrac{1}{5} u^5\right) + C =$$

$$\dfrac{1}{3} \left(\dfrac{1}{7}(\cos 3 x)^7 - \dfrac{1}{5} (\cos 3 x)^5\right) + C.\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{\sqrt{1 + x^2}}{x^4}\,dx$ .

Use trig substitution:

$$\int \dfrac{\sqrt{1 + x^2}}{x^4}\,dx = \int \dfrac{\sqrt{1 + (\tan \theta)^2}}{(\tan \theta)^4} (\sec \theta)^2\,d\theta = \int \dfrac{\sec \theta}{(\tan \theta)^4} (\sec \theta)^2\,d\theta = \int \dfrac{(\sec \theta)^3}{(\tan \theta)^4}\,d\theta =$$

$$\hfil\raise0.5in\hbox{$\left[x = \tan \theta, \quad dx = (\sec \theta)^2\,d\theta\right]$} \hskip0.5in \hbox{\epsfysize=1in \epsffile{integration-review-1.eps}}\hfil$$

$$\int \dfrac{1}{(\cos \theta)^3}\cdot \dfrac{(\cos \theta)^4}{(\sin \theta)^4}\,d\theta = \int \dfrac{\cos \theta}{(\sin \theta)^4}\,d\theta = \int \dfrac{\cos \theta}{u^4}\cdot \dfrac{du}{\cos \theta} = \int \dfrac{du}{u^4} =$$

$$\left[u = \sin \theta, \quad du = \cos \theta\,d\theta, \quad d\theta = \dfrac{du}{\cos \theta}\right]$$

$$-\dfrac{1}{3 u^3} + C = -\dfrac{1}{3(\sin \theta)^3} + C = -\dfrac{1}{3}\cdot \dfrac{(1 + x^2)^{3/2}}{x^3} + C.\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{1}{x + x^{7/9}}\,dx$ .

Let $x = u^9$ , so $dx = 9 u^8\,du$ .

$$\int \dfrac{1}{x + x^{7/9}}\,dx = \int \dfrac{9 u^8}{u^9 + u^7}\,du = 9 \int \dfrac{u}{u^2 + 1}\,du = 9 \int \dfrac{u}{w} \cdot \dfrac{dw}{2 u} = \dfrac{9}{2} \int \dfrac{1}{w}\,dw =$$

$$\left[w = u^2 + 1, \quad dw = 2 u\,du, \quad du = \dfrac{dw}{2 u}\right]$$

$$\dfrac{9}{2} \ln |w| + C = \dfrac{9}{2} \ln |u^2 + 1| + C = \dfrac{9}{2} \ln |x^{2/9} + 1| + C.$$

For the last step, I used the fact that $x = u^9$ gives $u = x^{1/9}$ , so $u^2 = x^{2/9}$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga