Miscellaneous Integration Techniques

In this section, I'll look at some other integration techniques.

Completing the square.

When an integral contains a quadratic expression $ax^2 + b x + c$ --- that is, a quadratic with a middle term $b x$ --- you can sometimes simplify the integrand by completing the square. This eliminates the middle term of the quadratic; the resulting integral can then be computed using (e.g.) trig substitution.

Example. Compute $\displaystyle \int \dfrac{1}{x^2 + 4 x + 13}\,dx$ .

Since $\dfrac{1}{2}\cdot 4 = 2$ and $2^2 = 4$ , I have

$$x^2 + 4 x + 13 = x^2 + 4 x + 4 + 9 = (x + 2)^2 + 9.$$

Therefore,

$$\int \dfrac{1}{x^2 + 4 x + 13}\,dx = \int \dfrac{1}{(x + 2)^2 + 9}\,dx = \int \dfrac{1}{u^2 + 9}\,du =$$

$$\left[u = x + 2, \quad du = dx\right]$$

$$\dfrac{1}{3} \tan^{-1} \dfrac{u}{3} + C = \dfrac{1}{3} \tan^{-1} \dfrac{x + 2}{3} + C.\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{\sqrt{x^2 + 2 x - 8}}{x + 1}\,dx$ .

Since $\dfrac{1}{2}\cdot 2 = 1$ and $1^2 = 1$ , I have

$$x^2 + 2 x - 8 = x^2 + 2 x + 1 - 9 = (x + 1)^2 - 9.$$

Therefore,

$$\int \dfrac{\sqrt{x^2 + 2 x - 8}}{x + 1}\,dx = \int \dfrac{\sqrt{(x + 1)^2 - 9}}{x + 1}\,dx = \int \dfrac{\sqrt{u^2 - 9}}{u}\,du.$$

$$\left[u = x + 1, \quad du = dx\right]$$

Next, I need a trig substitution:

$$\int \dfrac{\sqrt{u^2 - 9}}{u}\,du = \int \dfrac{\sqrt{9(\sec \theta)^2 - 9}}{3 \sec \theta} (3\sec \theta \tan \theta\,d\theta) = \int \dfrac{3 \tan \theta}{3 \sec \theta} (3\sec \theta \tan \theta\,d\theta) = 3 \int (\tan \theta)^2\,d\theta =$$

$$\hfil\raise0.5in\hbox{$\left[x = 3 \sec \theta, \quad dx = 3 \sec \theta \tan \theta\,d\theta\right]$} \hskip0.5in \hbox{\epsfysize=1in \epsffile{miscellaneous-integration-techniques-1.eps}}\hfil$$

$$3 \int \left((\sec \theta)^2 - 1\right)\,d\theta = 3 \left(\tan \theta - \theta\right) + C = 3 \left(\dfrac{\sqrt{u^2 - 9}}{3} - \sec^{-1} \dfrac{u}{3}\right) + C =$$

$$3 \left(\dfrac{\sqrt{(x + 1)^2 - 9}}{3} - \sec^{-1} \dfrac{x + 1}{3}\right) + C.\quad\halmos$$

Note that in some cases, an integral containing a quadratic with a middle term can be integrated in other ways. For example, in this integral I can let $u = x - 3$ :

$$\int \dfrac{1}{x^2 - 6 x + 9}\,dx = \int \dfrac{1}{(x - 3)^2}\,dx = -\dfrac{1}{x - 3} + C.$$

This integral can be done using partial fractions:

$$\int \dfrac{1}{x^2 - 5 x + 6}\,dx = \int \dfrac{1}{(x - 2)(x - 3)}\,dx = \int \left(\dfrac{1}{x - 3} - \dfrac{1}{x - 2}\right)\,dx = \ln |x - 3| - \ln |x - 2| + C.$$

Fractional powers.

When an integral contains fractional powers $x^{m/n}$ , you can often simplify the integrand using a substitution of the form

$$x = u^k.$$

Take k to be the least common multiple of the denominators of the fractions that occur in the exponent.

Example. Compute $\displaystyle \int \dfrac{dx}{x^{3/4} + x^{2/3}}$ .

Since the least common multiple of the denominators 3 and 4 is 12, I'll use $x = u^{12}$ :

$$\int \dfrac{dx}{x^{3/4} + x^{2/3}} = \int \dfrac{12 u^{11}\,du}{u^9 + u^8} = 12 \int \dfrac{u^3}{u + 1}\,du.$$

$$\left[x = u^{12}, \quad dx = 12 u^{11}\,du\right]$$

Since the top has a higher power than the bottom, I do a long division:

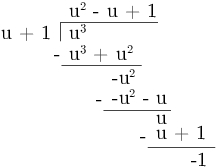
$$\hbox{\epsfysize=1.5 in \epsffile{miscellaneous-integration-techniques-2.eps}}$$

This gives

$$\dfrac{u^3}{u + 1} = u^2 - u + 1 - \dfrac{1}{u + 1}.$$

Hence, my integral is

$$12 \int \left(u^2 - u + 1 - \dfrac{1}{u + 1}\right)\,du =$$

$$12 \left(\dfrac{1}{3}u^3 - \dfrac{1}{2}u^2 + u - \ln |u + 1|\right) + C = 12 \left(\dfrac{1}{3}x^{1/4} - \dfrac{1}{2}x^{1/6} + x^{1/12} - \ln |x^{1/12} + 1|\right) + C.\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{dx}{x^{1/2}(x^{1/2} + 3 x^{1/5})}$ .

Since the least common multiple of the denominators 2 and 5 is 10, I'll use $x = u^{10}$ :

$$\int \dfrac{dx}{x^{1/2}(x^{1/2} + 3 x^{1/5})} = \int \dfrac{10 u^9\,du}{u^5(u^5 + 3 u^2)} = 10 \int \dfrac{u^2}{u^3 + 3}\,du = 10 \int \dfrac{u^2}{w}\cdot \dfrac{dw}{3 u^2} = \dfrac{10}{3} \int \dfrac{dw}{w} = \dfrac{10}{3} \ln |w| + C =$$

$$\left[x = u^{10}, \quad dx = 10 u^9\,du\right]\hskip0.5 in \left[w = u^3 + 3, \quad dw = 3 u^2\,du, \quad du = \dfrac{dw}{3 u^2}\right]$$

$$\dfrac{10}{3} \ln |u^3 + 3| + C = \dfrac{10}{3} \ln |x^{3/10} + 3| + C.\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{x}{\sqrt{x + 1}}\,dx$ .

The idea here is the same as in the last two examples: I can eliminate a square root by putting a square inside.

$$\int \dfrac{x}{\sqrt{x + 1}}\,dx = \int \dfrac{u^2 - 1}{\sqrt{u^2}}\cdot 2 u\,du = \int \dfrac{u^2 - 1}{u}\cdot 2 u\,du = 2 \int (u^2 - 1)\,du = 2\left(\dfrac{1}{3}u^3 - u\right) + C =$$

$$\left[x + 1 = u^2, \quad dx = 2 u\,du; \quad x = u^2 - 1, \quad u = (x + 1)^{1/2}\right]$$

$$\dfrac{2}{3}(x + 1)^{3/2} - 2\sqrt{x + 1} + C.\quad\halmos$$

Example. Compute $\displaystyle \int \cos \sqrt{x}\,dx$ .

Let $x = u^2$ , so $dx = 2 u\,du$ . I get

$$\int \cos \sqrt{x}\,dx = 2 \int u \cos u\,du.$$

I'll do this integral by parts:

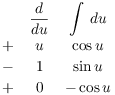
$$\matrix{ & \displaystyle \der {} u & \displaystyle \int\,du \cr \noalign{\vskip2pt} + & u & \cos u \cr \noalign{\vskip2pt} - & 1 & \sin u \cr \noalign{\vskip2pt} + & 0 & -\cos u \cr}$$

I do the parts computation and put the x's back using $u = \sqrt{x}$ (since $x = u^2$ ):

$$\int \cos \sqrt{x}\,dx = 2 \int u \cos u\,du = 2 \left(u \sin u + \cos u\right) + C = 2 \left(\sqrt{x} \sin \sqrt{x} + \cos \sqrt{x}\right) + C.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga