Parametric Equations of Curves

The parametric equations for a curve in the plane consists of a pair of equations

$$x = f(t), \quad y = g(t), \quad a \le t \le b.$$

Each value of the parameter t gives values for x and y; the point $(x, y)$ is the corresponding point on the curve.

For example, consider the parametric equations

$$x = t^2 + 1, \quad y = t^3 + t + 1.$$

Here are some points $(x, y)$ which result from plugging in some values for t:

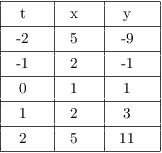
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & t & & x & & y & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & -2 & & 5 & & -9 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & -1 & & 2 & & -1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 0 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 5 & & 11 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The graph of the curve looks like this:

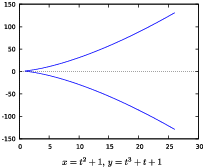
$$\hbox{\epsfysize=1.5in \epsffile{parametric-equations-1.eps}}$$

These are parametric equations for the circle $x^2 + y^2 = 1$ :

$$x = \cos t, \quad y = \sin t, \quad 0 \le t \le 2\pi$$

$$\hbox{\epsfysize=1.75in \epsffile{parametric-equations-2.eps}}$$

You can sometimes recover the x-y equation of a parametric curve by eliminating t from the parametric equations. In this case,

$$x^2 + y^2 = (\cos t)^2 + (\sin t)^2 = 1.$$

Notice that the graph of a circle is not the graph of a function. Parametric equations can represent more general curves than function graphs can, which is one of their advantages.

These parametric equations represent a spiral:

$$x = t \cos t, \quad y = t \sin t,$$

$$\hbox{\epsfysize=1.75in \epsffile{parametric-equations-3.eps}}$$

This is also not the graph of a function $y = f(x)$ .

Example. Find the x-y equation for

$$x = t^3 + 1, \quad y = t^2 + t + 1.$$

Solve the x-equation for t:

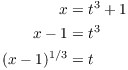
$$\eqalign{ x & = t^3 + 1 \cr x - 1 & = t^3 \cr (x - 1)^{1/3} & = t \cr}$$

Plug this expression for t into the y-equation:

$$y = (x - 1)^{2/3} + (x - 1)^{1/3} + 1.\quad\halmos$$

Example. Find the x-y equation for

$$x = 5 + 2\cos t, \quad y = -3 + \sin t.$$

Notice that

$$\cos t = \dfrac{x - 5}{2}, \quad \sin t = y + 3.$$

So

$$\left(\dfrac{x - 5}{2}\right)^2 + (y + 3)^2 = (\cos t)^2 + (\sin t)^2 = 1.$$

This is the standard form for the equation of an ellipse.

In some cases, recovering an x-y equation would be difficult or impossible. For example, these are the parametric equations for a hypocycloid of four cusps:

$$x = 3\cos t + \cos 3 t, \quad y = 3\sin t - \sin 3 t, \quad 0 \le t \le 2\pi$$

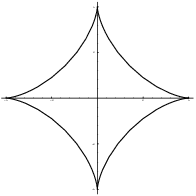
$$\hbox{\epsfysize=1.75in \epsffile{parametric-equations-4.eps}}$$

In this case, it would be difficult to eliminate t to obtain an x-y equation.

What about going the other way? If you have a curve (or an x-y equation), how do you obtain parametric equations?

Note first that a given curve can be represent by infinitely many sets of parametric equations. For example, all of these sets of parametric equations represent the unit circle $x^2 + y^2 = 1$ :

$$x = \cos t, \quad y = \sin t, \quad 0 \le t \le 2 \pi.$$

$$x = \cos 11 t, \quad y = \sin 11 t, \quad 0 \le t \le \dfrac{2 \pi}{11}.$$

$$x = -\sin t, \quad y = \cos t, \quad 0 \le t \le 2 \pi.$$

Even so, it can be difficult to find parametrizations for curves.

Let's start with an easy case. If you have x-y equations in which x or y is solved for, it's easy. For example, to parametrize $y = x^2$ , set $x = t$ . Then $y = x^2 = t^2$ . A parametrization is given by

$$x = t, \quad y = t^2.$$

To parametrize $x = 3 y - y^2$ , set $y = t$ . Then $x = 3 y - y^2 = 3 t - t^2$ , so

$$x = 3 t - t^2, \quad y = t.$$

This is a parametrization of $x = 3 y - y^2$ . (This is how you can graph x-in-terms-of-y equations on your calculator.)

Here's another important case. If $(a, b)$ and $(c, d)$ are points, the line through $(a, b)$ and $(c, d)$ may be parametrized by

$$x = a + t (c - a), \quad y = b + t (d - b), \quad -\infty < t < \infty.$$

It is easiest to remember this in the vector form

$$(x, y) = (1 - t) \cdot (a, b) + t \cdot (c, d).$$

Notice that when $t = 0$ , I have $(x, y) = (a, b)$ , and when $t = 1$ , $(x, y) = (c, d)$ . Thus, if you let $0 \le t \le 1$ , you get the segment from $(a, b)$ to $(c, d)$ .

Example. Find parametric equations for the line through $(3, -6)$ and $(5, 2)$ .

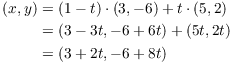
$$\eqalign{ (x, y) & = (1 - t) \cdot (3, -6) + t \cdot (5, 2) \cr & = (3 - 3 t, -6 + 6 t) + (5 t, 2 t) \cr & = (3 + 2 t, -6 + 8 t) \cr}$$

Thus,

$$x = 3 + 2 t \quad\hbox{and}\quad y = -6 + 8 t.\quad\halmos$$

An analogous result holds for lines in 3 dimensions (or in any number of dimensions).

As an example of a more general method of parametrizing curves, I'll consider parametrizing by slope. The idea is to think of a point $(x, y)$ on the curve as the intersection point of the curve and the line $y = x t$ :

$$\hbox{\epsfysize=1.75in \epsffile{parametric-equations-5.eps}}\quad\halmos$$

The slope t will be the parameter for the curve.

Example. Find parametric equations for the Folium of Descartes:

$$x^3 + y^3 = 3 x y.$$

Set $y = x t$ . Then

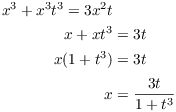
$$\eqalign{ x^3 + x^3 t^3 = 3 x^2 t \cr x + x t^3 & = 3 t \cr x(1 + t^3) & = 3 t \cr \noalign{\vskip2pt} x & = \dfrac{3 t}{1 + t^3} \cr}$$

Therefore, $y = x t = \dfrac{3 t^2}{1 + t^3}$ . A parametrization is given by

$$x = \dfrac{3 t}{1 + t^3}, \quad y = \dfrac{3 t^2}{1 + t^3}.$$

$$\hbox{\epsfysize=2in \epsffile{parametric-equations-6.eps}}\quad\halmos$$

The first and second derivatives give information about the shape of a curve. Here's how to find the derivatives for a parametric curve.

First, by the Chain Rule,

$$\der x t \cdot \der y x = \der y t.$$

Solving for $\der y x$ gives

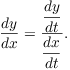
$$\der y x = \dfrac{\der y t}{\der x t}.$$

Example. Find the equation of the tangent line to the curve

$$x = e^t + t^2, \quad y = e^{2 t} + 3 t \quad\hbox{at}\quad t = 1.$$

$$\der y x = \dfrac{2 e^{2 t} + 3}{e^t + 2 t}, \quad\hbox{so}\quad \left.\der y x\right|_{t=1} = \dfrac{2 e^2 + 3}{e + 2}.$$

When $t = 1$ , $x = e + 1$ and $y = e^2 + 3$ . The tangent line is

$$y - (e^2 + 3) = \left(\dfrac{2 e^2 + 3}{e + 2}\right) (x - (e + 1)).\quad\halmos$$

Example. At what points on the following curve is the tangent line horizontal?

$$x = t^3 + t + 2, \quad y = 2 t^3 - 3 t^2 - 12 t + 5$$

Find the derivative:

$$\der y x = \dfrac{6 t^2 - 6 t - 12}{3 t^2 + 1} = \dfrac{6(t - 2)(t + 1)}{3 t^2 + 1}.$$

The tangent line is horizontal when $\der y x = 0$ , and $\der y x = 0$ for $t = 2$ and for $t = -1$ .

When $t = 2$ , $x = 12$ and $y = -15$ . When $t = -1$ , $x = 0$ and $y = 12$ . There are horizontal tangents are $(12, -15)$ and at $(0, 12)$ .

$$\hbox{\epsfysize=1.75in \epsffile{parametric-equations-7.eps}}\quad\halmos$$

To find the second derivative, I differentiate the first derivative.

$$\dfrac{d^2 y}{dx^2} = \der {} x \left(\der y x\right).$$

Since $\der y x$ will come out in terms of t, I want to be sure to differentiate $\der y x$ with respect to t. Use the Chain Rule again:

$$\der {} x \left(\der y x\right) = \der t x\cdot \left[\der {} t \left(\der y x\right)\right] = \dfrac{\der {} t \left(\der y x\right)}{\der x t}.$$

That is,

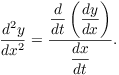
$$\dfrac{d^2 y}{dx^2} = \dfrac{\der {} t \left(\der y x\right)}{\der x t}.$$

Example. Find $\der y x$ and $\dfrac{d^2 y}{dx^2}$ at $t = 1$ for

$$x = t^2 + t + 2, \quad y = 2 t^3 - t + 5.$$

First,

$$\der x t = 2 t + 1, \quad \der y t = 6 t^2 - 1.$$

So

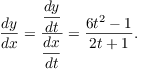
$$\der y x = \dfrac{\der y t}{\der x t} = \dfrac{6 t^2 - 1}{2 t + 1}.$$

When $t = 1$ , I have $\der y x = \dfrac{5}{3}$ .

Next,

$$\der {} t \left(\der y x\right) = \der {} t \dfrac{6 t^2 - 1}{2 t + 1} = \dfrac{(2 t + 1)(12 t) - (6 t^2 - 1)(2)}{(2 t + 1)^2}.$$

So

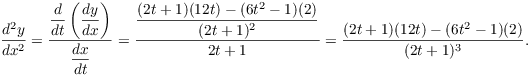
$$\dfrac{d^2 y}{dx^2} = \dfrac{\der {} t \left(\der y x\right)}{\der x t} = \dfrac{\dfrac{(2 t + 1)(12 t) - (6 t^2 - 1)(2)}{(2 t + 1)^2}}{2 t + 1} = \dfrac{(2 t + 1)(12 t) - (6 t^2 - 1)(2)}{(2 t + 1)^3}.$$

When $t = 1$ , I have $\dfrac{d^2 y}{dx^2} = \dfrac{26}{27}$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga