Partial Fractions

Partial fractions is the opposite of adding fractions over a common denominator. It applies to integrals of rational functions:

$$\int \dfrac{P(x)}{Q(x)}\,dx.$$

$P(x)$ and $Q(x)$ are polynomials.

The idea is to break $\dfrac{P(x)}{Q(x)}$ into a sum of smaller terms which are easier to integrate.

I'll start by doing a few examples to give you a feel for the procedure. Then I'll go back and explain the general method. These problems are sometimes a bit long, and require a substantial amount of algebra. Therefore, before using partial fractions, you should be sure that there isn't an easier way to do the integral.

First, I want to mention some integrals that often come up in these problems:

$$\int \dfrac{1}{a x + b}\,dx = \dfrac{1}{a} \ln |a x + b| + C, \quad a \ne 0.$$

(Do you see how to work it out? Substitute $u = a x + b$ , so $du = a\,dx$ .) For example,

$$\int \dfrac{1}{x - 7}\,dx = \ln |x - 7| + C,$$

$$\int \dfrac{1}{4 x + 5}\,dx = \dfrac{1}{4} \ln |4 x + 5| + C,$$

$$\int \dfrac{1}{3 - 2 x}\,dx = -\dfrac{1}{2} \ln |3 - 2 x| + C.$$

However,

$$\int \dfrac{1}{(a x + b)^2}\,dx = -\dfrac{1}{a} \dfrac{1}{a x + b} + C, \quad a \ne 0.$$

(Similar formulas hold for powers other than 2.) Once again, you can do this by letting $u = a x + b$ . Some examples:

$$\int \dfrac{1}{(x - 7)^2}\,dx = -\dfrac{1}{x - 7} + C.$$

$$\int \dfrac{1}{(4 x + 5)^2}\,dx = -\dfrac{1}{4} \dfrac{1}{4 x + 5} + C,$$

$$\int \dfrac{1}{(3 - 2 x)^2}\,dx = \dfrac{1}{2} \dfrac{1}{3 - 2 x} + C.$$

Example. Compute $\displaystyle \int \dfrac{17 - 3 x}{x^2 - 2 x - 3}\,dx$ .

$x^2 - 2 x - 3 = (x - 3)(x + 1)$ . Write

$$\dfrac{17 - 3 x}{(x - 3)(x + 1)} = \dfrac{a}{x - 3} + \dfrac{b}{x + 1}.$$

Multiply both sides by $(x - 3)(x + 1)$ to clear denominators:

$$17 - 3 x = a(x + 1) + b(x - 3).$$

Let $x = 3$ . I get

$$17 - 9 = 4 a + 0, \quad\hbox{so}\quad 8 = 4 a, \quad\hbox{or}\quad a = 2.$$

Let $x = -1$ . I get

$$17 + 3 = 0 - 4 b, \quad\hbox{so}\quad 20 = -4 b, \quad\hbox{or}\quad b = -5.$$

Therefore,

$$\dfrac{17 - 3 x}{(x - 3)(x + 1)} = \dfrac{2}{x - 3} - \dfrac{5}{x + 1}.$$

So

$$\int \dfrac{17 - 3 x}{x^2 - 2 x - 3}\,dx = \int \left(\dfrac{2}{x - 3} - \dfrac{5}{x + 1}\right)\,dx = 2 \ln |x - 3| - 5 \ln |x + 1| + C.\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{5 x^2 - 28 x + 31}{(x - 1)^2 (x - 5)}\,dx$ .

This example will show how to handle repeated factors --- in this case, $(x - 1)^2$ . Here's what you do:

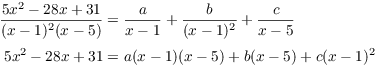
$$\eqalign{ \dfrac{5 x^2 - 28 x + 31}{(x - 1)^2 (x - 5)} & = \dfrac{a}{x - 1} + \dfrac{b}{(x - 1)^2} + \dfrac{c}{x - 5} \cr \noalign{\vskip2 pt} 5 x^2 - 28 x + 31 & = a (x - 1)(x - 5) + b (x - 5) + c (x - 1)^2 \cr}$$

Notice that on the right side, I have two terms corresponding to $(x - 1)^2$ , namely

$$\dfrac{a}{x - 1} \quad\hbox{and}\quad \dfrac{b}{(x - 1)^2}.$$

Why do I need both? I mentioned that partial fractions is the opposite of combining fractions over a common denominator. So I start with $\dfrac{5 x^2 - 28 x + 31}{(x - 1)^2 (x - 5)}$ and ask: What fractions combined to give this? Well, fractions of these three kinds could combine to give this:

$$\dfrac{a}{x - 1}, \quad \dfrac{b}{(x - 1)^2}, \quad \dfrac{c}{x - 5}.$$

I have to include all three in my decomposition because I have to allow for all possibilities.

Set $x = 1$ . This gives

$$8 = b \cdot -4, \quad\hbox{so}\quad b = -2.$$

Set $x = 5$ . This gives

$$16 = c \cdot 16, \quad\hbox{so}\quad c = 1.$$

Plugging the values for b and c back in yields

$$5 x^2 - 28 x + 31 = a (x - 1)(x - 5) + -2 (x - 5) + 1 (x - 1)^2.$$

Set $x = 0$ . This gives

$$31 = a \cdot 5 - -10 + 1, \quad\hbox{so}\quad a = 4.$$

Thus,

$$\dfrac{5 x^2 - 28 x + 31}{(x - 1)^2 (x - 5)} = \dfrac{4}{x - 1} + \dfrac{-2}{(x - 1)^2} + \dfrac{1}{x - 5}.$$

Hence,

$$\int \dfrac{5 x^2 - 28 x + 31}{(x - 1)^2 (x - 5)}\,dx = \int \left(\dfrac{4}{x - 1} + \dfrac{-2}{(x - 1)^2} + \dfrac{1}{x - 5}\right)\,dx =$$

$$4 \ln |x - 1| - \dfrac{-2}{x - 1} + \ln |x - 5| + C.\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{2 - x^2}{x(x - 1)^2}\,dx$ .

$$\dfrac{2 - x^2}{x(x - 1)^2} = \dfrac{a}{x} + \dfrac{b}{x - 1} + \dfrac{c}{(x - 1)^2}.$$

For a repeated factor, you have one term for each power up to the power the factor is raised to. In this case, you have a term for $x - 1$ and a term for $(x - 1)^2$ .

Multiply to clear denominators:

$$2 - x^2 = a(x - 1)^2 + b x(x - 1) + c x.$$

Let $x = 0$ . I get $2 = a$ .

Let $x = 1$ . I get $1 = c$ .

Plug the a and c values back in:

$$2 - x^2 = 2 (x - 1)^2 + b x(x - 1) + x.$$

With only b left, I can plug in any number and solve for b. I'll let $x = 2$ :

$$2 - 4 = 2 + 2 b + 2, \quad -6 = 2 b, \quad b = -3.$$

Therefore,

$$\dfrac{2 - x^2}{x(x - 1)^2} = \dfrac{2}{x} - \dfrac{3}{x - 1} + \dfrac{1}{(x - 1)^2}.$$

Hence,

$$\int \dfrac{2 - x^2}{x(x - 1)^2}\,dx = \int \left(\dfrac{2}{x} - \dfrac{3}{x - 1} + \dfrac{1}{(x - 1)^2}\right)\,dx = 2 \ln |x| - 3 \ln |x - 1| - \dfrac{1}{x - 1} + C.$$

Here's another way you can proceed from the last b-equation. I'll multiply out the b-term first:

$$\eqalign{ 2 - x^2 & = 2 (x - 1)^2 + b x(x - 1) + x \cr 2 - x^2 & = 2 (x - 1)^2 + b (x^2 - x) + x \cr}$$

Since this is an identity, I can differentiate both sides:

$$-2 x = 4(x - 1) + b(2 x - 1) + 1.$$

(I multiplied out the b-term to avoid the Product Rule, but this isn't essential.)

Now I can recycle $x = 1$ . Plugging in $x = 1$ gives $-2 = b + 1$ , so $b = -3$ as before.

Let's repeat the point we saw in the last example: At any point in solving for the coefficients, you can plug in an arbitrary number for x, or you can differentiate both sides of the equation. You can even use both. Use whatever approach seems to be easier.

Example. Compute $\displaystyle \int \dfrac{5 x^2 - 19 x + 20}{x^3 - 5 x^2}$ .

Note that

$$x^3 - 5 x^2 = x^2 (x - 5).$$

Set up the partial fractions decomposition:

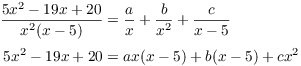
$$\eqalign{ \dfrac{5 x^2 - 19 x + 20}{x^2 (x - 5)} & = \dfrac{a}{x} + \dfrac{b}{x^2} + \dfrac{c}{x - 5} \cr \noalign{\vskip2pt} 5 x^2 - 19 x + 20 & = a x (x - 5) + b (x - 5) + c x^2 \cr}$$

Set $x = 0$ . This gives

$$20 = -5 b, \quad\hbox{so}\quad b = -4.$$

Set $x = 5$ . This gives

$$50 = 25 c, \quad\hbox{so}\quad c = 2.$$

Plug $b = -4$ and $c = 2$ back in to get

$$\eqalign{ 5 x^2 - 19 x + 20 & = a x (x - 5) - 4 (x - 5) + 2 x^2 \cr}$$

Now set x to any number (besides 0 or 5, which you already used). I'll use $x = 1$ , since it makes the computations easy:

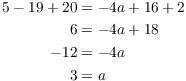
$$\eqalign{ 5 - 19 + 20 & = -4 a + 16 + 2 \cr 6 & = -4 a + 18 \cr -12 & = -4 a \cr 3 & = a \cr}$$

Compute the integral:

$$\int \dfrac{5 x^2 - 19 x + 20}{x^2 (x - 5)} = \int \left(\dfrac{3}{x} - \dfrac{4}{x^2} + \dfrac{2}{x - 5}\right)\,dx =$$

$$3 \ln |x| + \dfrac{4}{x} + 2 \ln |x - 5| + C.\quad\halmos$$

There are some cases I haven't considered yet, specifically what you do if you have a term like $x^2 + 4$ in the denominator. ($x^2 + 4$ doesn't factor into linear factors, at least not with real numbers.)

However, I'll pause to describe the steps in the method in more detail.

Suppose $P(x)$ and $Q(x)$ are polynomials. Consider an integral of the form

$$\int \dfrac{P(x)}{Q(x)}\,dx.$$

Recall that the degree of a polynomial is the highest power of the variable that occurs in it. Nonzero constants have degree 0; by convention, 0 has degree $-\infty$ .

Step 1. If the degree of the top is greater than or equal to the degree of the bottom, divide the bottom into the top.

Step 2. You will now have an integral that looks like $\displaystyle \int \dfrac{P(x)}{Q(x)}\,dx$ , where $P(x)$ and $Q(x)$ are polynomials, and the top is smaller in degree than the bottom.

Factor the bottom of the fraction into a product of linear terms and irreducible quadratic terms.

A linear term is a term where the variable occurs only to the first power. Here are some linear terms:

$$x - 1, \quad 2 x - 3, \quad x.$$

An irreducible quadratic term is a quadratic term with only imaginary (complex) roots. That is, it is a quadratic which "doesn't factor". Here are some irreducible quadratic terms:

$$x^2 + 1, \quad x^2 - 2 x + 5.$$

However, $x^2 - 5 x - 6$ is not an irreducible quadratic, because it factors:

$$x^2 - 5 x - 6 = (x - 6)(x + 1).$$

Likewise, $x^2 - 2$ is not irreducible:

$$x^2 - 2 = (x - \sqrt{2})(x + \sqrt{2}).$$

("Ugly" factors are allowed.) And $x^2$ is not considered an irreducible quadratic: It is $(x - 0)(x - 0)$ , the square of a linear term. This distinction will become important in Step 3.

You can check that a quadratic is irreducible by using the quadratic formula to find its roots. If the roots are complex numbers, the quadratic does not factor.

Step 3. Obtain the partial fractions decomposition for the fraction.

This is the heart of the partial fractions method. It is basically a lot of algebra, but it's sufficiently complicated that the best way to describe it is by doing some examples.

Step 4. Compute the integrals for the fractions you obtained in Step 3.

Since we've already seen examples which involve the decomposition in Step 3, I'll give some examples where you need to divide first.

Example. Compute $\displaystyle \int \dfrac{2 x^3 - 5 x^2 - x + 5}{x^2 - 1}\,dx$ .

The top has degree 3 while the bottom has degree 2. Divide the bottom into the top:

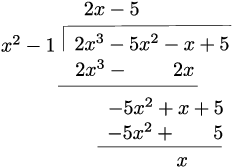
$$\hbox{\epsfysize=1.5in \epsffile{partial-fractions-1.eps}}$$

$$\dfrac{2 x^3 - 5 x^2 - x + 5}{x^2 - 1} = 2 x - 5 + \dfrac{x}{x^2 - 1}.$$

(This is "polynomial long division" --- you probably saw it [and perhaps forgot it!] in high school algebra.)

So

$$\int \dfrac{2 x^3 - 5 x^2 - x + 5}{x^2 - 1}\,dx = \int \left(2 x - 5 + \dfrac{x}{x^2 - 1}\right)\,dx.$$

Integrate $\dfrac{x}{x^2 - 1}$ by substitution:

$$\int \dfrac{x}{x^2 - 1} \,dx = \dfrac{1}{2} \int \dfrac{du}{u} = \dfrac{1}{2} \ln |u| + C = \dfrac{1}{2} \ln |x^2 - 1| + C.$$

$$\left[u = x^2 - 1, \quad du = 2 x\,dx, \quad dx = \dfrac{du}{2 x}\right]$$

Hence,

$$ \int \left(2 x - 5 + \dfrac{x}{x^2 - 1}\right)\,dx = x^2 - 5 x + \dfrac{1}{2} \ln |x^2 - 1| + C.$$

In this problem, division simplified the integral enough that it wasn't necessary to go any further in the partial fractions procedure.

Example. Compute $\displaystyle \int \dfrac{x^2}{x^2 - 1}\,dx$ .

The top and the bottom have the same degree, so I must divide the bottom into the top. I could do a polynomial long division as in the previous example, but here's an algebra trick that is sometimes useful:

$$\dfrac{x^2}{x^2 - 1} = \dfrac{(x^2 - 1) + 1}{x^2 - 1} = \dfrac{x^2 - 1}{x^2 - 1} + \dfrac{1}{x^2 - 1} = 1 + \dfrac{1}{x^2 - 1}.$$

Therefore,

$$ \int \dfrac{x^2}{x^2 - 1}\,dx = \int \left(1 + \dfrac{1}{x^2 - 1}\right)\,dx.$$

I can do $\displaystyle \int 1\,dx$ easily; I need to integrate the second term. Factor the denominator: $\dfrac{1}{x^2 - 1} = \dfrac{1}{(x - 1)(x + 1)}$ . Then

$$\dfrac{1}{(x - 1)(x + 1)} = \dfrac{a}{x - 1} + \dfrac{b}{x + 1}, \quad\hbox{so}\quad 1 = a(x - 1) + b(x + 1).$$

Let $x = 1$ . I get $1 = 2 b$ , so $b = \dfrac{1}{2}$ .

Let $x = -1$ . I get $1 = -2 a$ , so $a = -\dfrac{1}{2}$ .

Thus,

$$\dfrac{1}{x^2 - 1} = -\dfrac{1}{2}\cdot \dfrac{1}{x - 1} + \dfrac{1}{2}\cdot \dfrac{1}{x + 1}.$$

Therefore,

$$\int \left(1 + \dfrac{1}{x^2 - 1}\right)\,dx = \int \left(1 - \dfrac{1}{2}\cdot \dfrac{1}{x - 1} + \dfrac{1}{2}\cdot \dfrac{1}{x + 1}\right)\,dx = x - \dfrac{1}{2} \ln |x - 1| + \dfrac{1}{2} \ln |x + 1| + C.\quad\halmos$$

Long division in Step 1 is a preliminary operation which puts the integral into the right form for the rest of the procedure. If you do a division, check before going on to see whether you can use a simple technique (like substitution) to do the integrals you've obtained. Sometimes you can complete the integration immediately; otherwise, you'll need to go on to Step 2.

Before I do another integral, I'll give some examples which show (as in the last integral) how you handle repeated factors (factors on the bottom that are raised to powers greater than 1).

Example. How would you try to decompose this rational function using partial fractions?

$$\dfrac{5 x^4 - 3 x + 1}{(x - 3)^4 (x + 2)^2}$$

That is, what is the initial partial fractions equation? (You don't need to do an integral.)

The linear factor $x - 3$ is repeated 4 times, and the linear factor $x + 2$ is repeated 2 times. So you use

$$\dfrac{5 x^4 - 3 x + 1}{(x - 3)^4(x + 2)^2} = \dfrac{a}{x - 3} + \dfrac{b}{(x - 3)^2} + \dfrac{c}{(x - 3)^3} + \dfrac{d}{(x - 3)^4} + \dfrac{e}{x + 2} + \dfrac{f}{(x + 2)^2}.$$

You could do the $x + 2$ terms first instead. Notice that the numerator $5 x^4 - 3 x + 1$ has no effect on the decomposition.

Example. How would you try to decompose this rational function using partial fractions?

$$\dfrac{3 x^3 + 4 x - 17}{x^3(2 x - 1)^2}$$

That is, what is the initial partial fractions equation? (You don't need to do an integral.)

The linear factor x is repeated 3 times and the linear factor $2 x - 1$ is repeated twice. Therefore, you should try to solve

$$\dfrac{3 x^3 + 4 x - 17}{x^3(2 x - 1)^2} = \dfrac{a}{x} + \dfrac{b}{x^2} + \dfrac{c}{x^3} + \dfrac{d}{2 x - 1} + \dfrac{e}{(2 x - 1)^2}.$$

Notice that the top of the fraction is irrelevant in deciding how to set up the decomposition. It only comes in during the solution process.

Notice also that "$x^3$ " is considered a linear term (x) raised to the third power. You get one term on the right for x, one for $x^2$ , and one for $x^3$ --- no "skipping"!

The next example shows how you might deal with an irreducible quadratic factor on the bottom.

Example. Compute $\displaystyle \int \dfrac{9 + 9 x - x^2}{(x - 5)(x^2 + 4)}\,dx$ .

The quadratic factor $x^2 + 4$ is irreducible. Here's how I try to decompose the fraction:

$$\dfrac{9 + 9 x - x^2}{(x - 5)(x^2 + 4)} = \dfrac{a}{x - 5} + \dfrac{b x + c}{x^2 + 4}.$$

Thus, a quadratic factor (or a quadratic factor to a power) will produce terms on the right with "two letters" on top.

The rationale is the same as the one I gave for repeated factors. I don't know what kind of fraction to expect, so I have to take the most general case.

Clear denominators:

$$9 + 9 x - x^2 = a(x^2 + 4) + (b x + c)(x - 5).$$

Let $x = 5$ . I get $29 = 29 a$ , so $a = 1$ . Plug $a = 1$ back in:

$$9 + 9 x - x^2 = (x^2 + 4) + (b x + c)(x - 5).$$

Let $x = 0$ . I get $9 = 4 - 5 c$ , so $5 = -5 c$ , or $c = -1$ . Plug $c = -1$ back in:

$$9 + 9 x - x^2 = (x^2 + 4) + (b x - 1)(x - 5).$$

At this point, I've run out of "nice" numbers to plug in for x. Since I have only one letter left ("b"), I can plug another value in for x, or I can differentiate.

For example, plugging in $x = 1$ gives

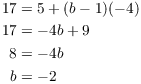
$$\eqalign{ 17 & = 5 + (b - 1)(-4) \cr 17 & = -4 b + 9 \cr 8 & = -4 b \cr b & = -2 \cr}$$

On the other hand, if I differentiate, I get

$$\eqalign{ 9 + 9 x - x^2 & = (x^2 + 4) + (b x - 1)(x - 5) \cr 9 - 2 x & = 2 x + b(x - 5) + (b x - 1) \cr}$$

(I got two b-terms by applying the Product Rule to $(b x - 1)(x - 5)$ .) Now I can recycle an old x-value, say $x = 0$ . Plugging this in gives $9 = -5 b - 1$ , or $10 = -5 b$ , so $b = -2$ again.

Thus,

$$\int \dfrac{9 + 9 x - x^2}{(x - 5)(x^2 + 4)}\,dx = \int \left(\dfrac{1}{x - 5} - \dfrac{2 x + 1}{x^2 + 4}\right)\,dx = \int \left(\dfrac{1}{x - 5} - \dfrac{2 x}{x^2 + 4} - \dfrac{1}{x^2 + 4}\right)\,dx =$$

$$\ln |x - 5| - \ln |x^2 + 4| - \dfrac{1}{2} \tan^{-1} \dfrac{x}{2} + C.$$

The first and third terms come from basic formulas. I integrated the second term using the substitution $u = x^2 + 4$ .

You handle repeated quadratic factors just as you handle repeated linear factors.

Example. How would you try to decompose this rational function using partial fractions?

$$\dfrac{2 x^2 + 3 x + 5}{(x^2 + 4)^3}$$

That is, what is the initial partial fractions equation? (You don't need to do an integral.)

The quadratic $x^2 + 4$ is irreducible. Try the decomposition

$$\dfrac{2 x^2 + 3 x + 5}{(x^2 + 4)^3} = \dfrac{a x + b}{x^2 + 4} + \dfrac{c x + d}{(x^2 + 4)^2} + \dfrac{e x + f}{(x^2 + 4)^3}.\quad\halmos$$

I will say candidly that you're very unlikely to have to work out something as complicated as the last example by hand: The algebra would be terrible! For something like this, you would probably use a computer algebra system.

Example. Compute $\displaystyle \int \dfrac{x^2 - 11 x + 8}{(x + 3)(x^2 + 1)}\,dx$ .

Try the decomposition

$$\dfrac{x^2 - 11 x + 8}{(x + 3)(x^2 + 1)} = \dfrac{a}{x + 3} + \dfrac{b x + c}{x^2 + 1}, \quad\hbox{so}\quad x^2 - 11 x + 8 = a(x^2 + 1) + (b x + c)(x + 3).$$

Let $x = -3$ . I get $50 = 10 a$ , so $a = 5$ . Plug $a = 5$ back in to obtain

$$x^2 - 11 x + 8 = 5(x^2 + 1) + (b x + c)(x + 3).$$

Let $x = 0$ . I get $8 = 5 + 3 c$ , so $c = 1$ . Plug $c = 1$ back in to obtain

$$x^2 - 11 x + 8 = 5(x^2 + 1) + (b x + 1)(x + 3).$$

I can differentiate both sides, or I can plug in another value of x. I'll plug in $x = 1$ . Doing so gives $-2 = 10 + 4(b + 1)$ , or $-2 = 14 + 4 b$ , so $b = -4$ .

Thus, the integral becomes

$$\int \dfrac{x^2 - 11 x + 8}{(x + 3)(x^2 + 1)}\,dx = \int \left(\dfrac{5}{x + 3} + \dfrac{-4 x + 1}{x^2 + 1}\right)\,dx = \int \left(\dfrac{5}{x + 3} - \dfrac{4 x}{x^2 + 1} + \dfrac{1}{x^2 + 1}\right)\,dx =$$

$$5 \ln |x + 3| - 2 \ln |x^2 + 1| + \tan^{-1} x + C.$$

The first and third terms are integrated using basic formulas; the second term is integrated using the substitution $u = x^2 + 1$ .

In the next example, none of the "easy" approaches work completely, so I have to resort to solving systems of equations.

Example. Compute $\displaystyle \int \dfrac{40 - 6 x - 6 x^3}{(x^2 + 1)(x^2 + 9)}\,dx$ .

Try the decomposition

$$\dfrac{40 - 6 x - 6 x^3}{(x^2 + 1)(x^2 + 9)} = \dfrac{a x + b}{x^2 + 1} + \dfrac{c x + d}{x^2 + 9}, \quad\hbox{so}\quad 40 - 6 x - 6 x^3 = (a x + b)(x^2 + 9) + (c x + d)(x^2 + 1).$$

In this case, there is no value of x I can plug in which will allow me to solve for one of a, b, c, d immediately. Therefore, I'll have to plug in and get equations, which I'll solve simultaneously later.

Let $x = 0$ . This gives $40 = 9 b + d$ .

Differentiate the equation to obtain

$$-6 - 18 x^2 = a (x^2 + 9) + 2 x (a x + b) + c(x^2 + 1) + 2 x (c x + d).$$

Let $x = 0$ . This gives $-6 = 9 a + c$ .

Before I differentiate again, I'll multiply the $2 x$ -terms in, so that I can avoid using the Product Rule:

$$-6 - 18 x^2 = a (x^2 + 9) + 2 a x^2 + 2 b x + c (x^2 + 1) + 2 c x^2 + 2 d x.$$

Differentiate:

$$-36 x = 2 a x + 4 a x + 2 b + 2 c x + 4 c x + 2 d.$$

Let $x = 0$ . This gives $0 = 2 b + 2 d$ , or $b + d = 0$ .

I now have two equations involving b and d, so I can solve for them. For instance, $b + d = 0$ gives $b = -d$ . Plug this into $40 = 9 b + d$ to obtain $40 = -9 d + d$ , or $d = -5$ . Then $b = -d$ gives $b = 5$ . Thus,

$$-36 x = 2 a x + 4 a x + 10 + 2 c x + 4 c x - 10.$$

Differentiate one more time and simplify:

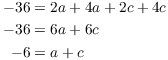
$$\eqalign{ -36 & = 2 a + 4 a + 2 c + 4 c \cr -36 & = 6 a + 6 c \cr -6 & = a + c \cr}$$

I'll solve simultaneously with $-6 = 9 a + c$ , this time using the "whole equation" approach:

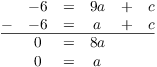
$$\matrix{& -6 & = & 9 a & + & c \cr - & -6 & = & a & + & c \cr \noalign{\vskip2 pt\hrule\vskip2 pt} & 0 & = & 8 a & & \cr & 0 & = & a & & \cr}$$

Plugging $a = 0$ into $-6 = a + c$ gives $c = -6$ .

Therefore, the integral becomes

$$\int \dfrac{40 - 6 x - 6 x^3}{(x^2 + 1)(x^2 + 9)}\,dx = \int \left(\dfrac{5}{x^2 + 1} - \dfrac{6 x + 5}{x^2 + 9}\right)\,dx = \int \left(\dfrac{5}{x^2 + 1} - \dfrac{6 x}{x^2 + 9} - \dfrac{5}{x^2 + 9}\right)\,dx =$$

$$5 \tan^{-1} x - 3 \ln |x^2 + 9| - \dfrac{5}{3} \tan^{-1} \dfrac{x}{3} + C.$$

The first and third terms are integrated using basic formulas. The second term is integrated using the substitution $u = x^2 + 9$ .

In the next example, I have an irreducible quadratic with a middle term. I'll need to complete the square.

Example. Compute $\displaystyle \int \dfrac{2 x^2 + x + 11}{(x + 3)(x^2 + 2 x + 10)}\,dx$ .

The quadratic $x^2 + 2 x + 10$ does not factor. Try the decomposition

$$\dfrac{2 x^2 + x + 11}{(x + 3)(x^2 + 2 x + 10)} = \dfrac{a}{x + 3} + \dfrac{bx + c}{x^2 + 2 x + 10}, \quad\hbox{so}\quad 2 x^2 + x + 11 = a(x^2 + 2 x + 10) + (b x + c)(x + 3).$$

Let $x = -3$ . I get $26 = 13 a$ , so $a = 2$ . Plug $a = 2$ back in to obtain

$$2 x^2 + x + 11 = 2(x^2 + 2 x + 10) + (b x + c)(x + 3).$$

Let $x = 0$ . I get $11 = 20 + 3 c$ , so $c = -3$ . Plug $c = -3$ back in to obtain

$$2 x^2 + x + 11 = 2(x^2 + 2 x + 10) + (b x - 3)(x + 3).$$

Differentiate:

$$4 x + 1 = 2(2 x + 2) + ( bx - 3)(1) + b(x + 3).$$

Let $x = 0$ . I get $1 = 4 - 3 + 3 b$ . so $b = 0$ .

Therefore, the integral becomes

$$\int \dfrac{2 x^2 + x + 11}{(x + 3)(x^2 + 2 x + 10)}\,dx = \int \left(\dfrac{2}{x + 3} - \dfrac{3}{x^2 + 2 x + 10}\right)\,dx.$$

I'll do the second term separately, since the first term is easy. The idea is to complete the square, then do a substitution:

$$\int \dfrac{3}{x^2 + 2 x + 10}\,dx = 3 \int \dfrac{1}{(x + 1)^2 + 9}\,dx = 3 \int \dfrac{1}{u^2 + 9}\,du = \tan^{-1} \dfrac{u}{3} + C = \tan^{-1} \dfrac{x + 1}{3} + C.$$

$$\left[u = x + 1, \quad du = dx\right]$$

Hence,

$$\int \left(\dfrac{2}{x + 3} - \dfrac{3}{x^2 + 2 x + 10}\right)\,dx = 2 \ln |x + 3| - \tan^{-1} \dfrac{x + 1}{3} + C.\quad\halmos$$

The next example involves some complicated integration, which you can skip if you're not interested. But try to understand how the partial fractions decomposition is done.

Example. Compute $\displaystyle \int \dfrac{1}{x^3 - 1}\,dx$ .

First,

$$\dfrac{1}{x^3 - 1} = \dfrac{1}{(x - 1)(x^2 + x + 1)}.$$

In this example, there's an irreducible quadratic factor $x^2 + x + 1$ . I try the decomposition

$$\dfrac{1}{(x - 1)(x^2 + x + 1)} = \dfrac{a}{x - 1} + \dfrac{b x + c}{x^2 + x + 1}.$$

Clear denominators:

$$1 = a(x^2 + x + 1) + (b x + c)(x - 1).$$

Let $x = 1$ . Then $1 = 3 a$ , so $a = \dfrac{1}{3}$ . Plug it back in:

$$1 = \dfrac{1}{3}(x^2 + x + 1) + (b x + c)(x - 1).$$

Let $x = 0$ . I get $1 = \dfrac{1}{3} - c$ , so $c = -\dfrac{2}{3}$ . Plug it back in:

$$1 = \dfrac{1}{3} (x^2 + x + 1) + (b x - \dfrac{2}{3})(x - 1).$$

Now I can either plug in a value for x at random, or differentiate. I'll differentiate:

$$0 = \dfrac{1}{3} (2 x + 1) + (b x - \dfrac{2}{3}) + b(x - 1).$$

Differentiate again:

$$0 = \dfrac{2}{3} + b + b.$$

This gives $b = -1/3$ .

Plug the values back into the original fractional decomposition:

$$\dfrac{1}{(x - 1)(x^2 + x + 1)} = \dfrac{1}{3}\ \dfrac{1}{x - 1} - \dfrac{1}{3}\ \dfrac{x + 2}{x^2 + x + 1}.$$

The integral is

$$\int \dfrac{1}{(x - 1)(x^2 + x + 1)}\,dx = \int \left(\dfrac{1}{3}\cdot \dfrac{1}{x - 1} - \dfrac{1}{3}\cdot \dfrac{x + 2}{x^2 + x + 1}\right)\,dx.$$

I'll do the integrals separately. First,

$$\int \dfrac{1}{3}\cdot \dfrac{1}{x - 1} = \dfrac{1}{3} \ln |x - 1| + C.$$

Next,

$$\dfrac{1}{3} \int \dfrac{x + 2}{x^2 + x + 1}\,dx = \dfrac{1}{6} \int \dfrac{2 x + 4}{x^2 + x + 1}\,dx = \dfrac{1}{6} \int \dfrac{2 x + 1 + 3}{x^2 + x + 1}\,dx =$$

$$\dfrac{1}{6} \left(\int \dfrac{2 x + 1}{x^2 + x + 1}\,dx + 3 \int \dfrac{1}{x^2 + x + 1}\,dx\right).$$

I can do the first integral using a substitution:

$$\int \dfrac{2 x + 1}{x^2 + x + 1}\,dx = \int \dfrac{du}{u} = \ln |u| + C = \ln |x^2 + x + 1| + C.$$

$$\left[u = x^2 + x + 1, \quad du = (2 x + 1)\,dx,\quad dx = \dfrac{du}{2 x + 1}\right]$$

The second requires completing the square:

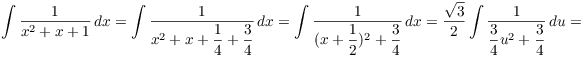
$$\int \dfrac{1}{x^2 + x + 1}\,dx = \int \dfrac{1}{x^2 + x + \dfrac{1}{4} + \dfrac{3}{4}}\,dx = \int \dfrac{1}{(x + \dfrac{1}{2})^2 + \dfrac{3}{4}}\,dx = \dfrac{\sqrt{3}}{2} \int \dfrac{1}{\dfrac{3}{4} u^2 + \dfrac{3}{4}}\,du =$$

$$\left[x + \dfrac{1}{2} = \dfrac{\sqrt{3}}{2}u, \quad dx = \dfrac{\sqrt{3}}{2}\,du\right]$$

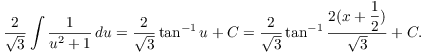
$$\dfrac{2}{\sqrt{3}} \int \dfrac{1}{u^2 + 1}\,du = \dfrac{2}{\sqrt{3}} \tan^{-1} u + C = \dfrac{2}{\sqrt{3}} \tan^{-1} \dfrac{2(x + \dfrac{1}{2})}{\sqrt{3}} + C.$$

Putting the two together,

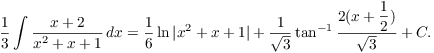
$$\dfrac{1}{3} \int \dfrac{x + 2}{x^2 + x + 1}\,dx = \dfrac{1}{6} \ln |x^2 + x + 1| + \dfrac{1}{\sqrt{3}} \tan^{-1} \dfrac{2(x + \dfrac{1}{2})}{\sqrt{3}} + C.$$

Finally, answer to the original problem is

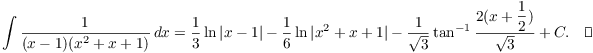
$$\int \dfrac{1}{(x - 1)(x^2 + x + 1)}\,dx = \dfrac{1}{3} \ln |x - 1| - \dfrac{1}{6} \ln |x^2 + x + 1| - \dfrac{1}{\sqrt{3}} \tan^{-1} \dfrac{2(x + \dfrac{1}{2})}{\sqrt{3}} + C.\quad\halmos$$

The last problem represents the limit (or depending on your point of view, the bottom of the barrel) in terms of the complexity of problems of this type. It points out why you should try easier integration techniques before you try partial fractions. And in really complicated cases, perhaps it's best to use a computer.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga