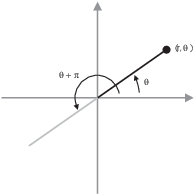
Polar Coordinates

Polar coordinates are an alternative to rectangular coordinates for referring to points in the plane. A point in the plane has polar coordinates $(r,\theta)$ . r is (roughly) the distance from the origin to the point; $\theta$ is the angle between the radius vector for the point and the positive x-axis. (As usual, angles are positive if measured counterclockwise and negative if measured clockwise.)

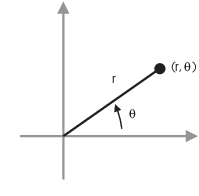
$\hbox{\epsfysize=1.75in \epsffile{polar-coordinates-1.eps}}$

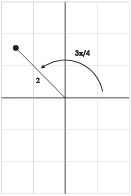
Example. Plot the points whose polar coordinates are:

(a) $\left(2, \dfrac{3 \pi}{4}\right)$ .

(b) $\left(-2, \dfrac{7 \pi}{6}\right)$ .

(a) To plot $\left(2, \dfrac{3 \pi}{4}\right)$ , rotate the x-axis through an angle of $\dfrac{3 \pi}{4}$ --- counterclockwise, since the angle is positive. Then go out 2 units.

$\hbox{\epsfysize=1.75in \epsffile{polar-coordinates-2.eps}}$

(b) To plot $\left(-2, \dfrac{7 \pi}{6}\right)$ , rotate the x-axis through an angle of $\dfrac{7 \pi}{6}$ .

$\hbox{\epsfysize=1.75in \epsffile{polar-coordinates-3.eps}}$

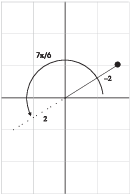
Locate the point -2 on the rotated x-axis. That is the point $\left(-2, \dfrac{7 \pi}{6}\right)$ .

$\hbox{\epsfysize=1.75in \epsffile{polar-coordinates-4.eps}}$

If you're plotting lots of points, you can do this rotation trick with a ruler, or you can make a little number line out of cardboard. If you do this, it's nearly impossible to get confused by points which have negative r's.

A point can be represented by infinitely many polar coordinate pairs.

If you add multiples of $2 \pi$ to the angle, you get the same point. For example, these are the same point in polar coordinates.

$\left(17, \dfrac{51 \pi}{4}\right) \quad\hbox{and}\quad \left(17, \dfrac{51 \pi}{4} + 6 \pi\right).$

If you multiply r by -1 and add $\pi$ to $\theta$ , you get the same point.

$\hbox{\epsfysize=1.75in \epsffile{polar-coordinates-5.eps}}$

Reason: Adding $\pi$ to $\theta$ and multiplying r by -1 each have the effect of "flipping" the point to the other side of the origin, so the two changes cancel out.

For example, these represent the same point in polar coordinates:

$\left(17, \dfrac{51 \pi}{4}\right) \quad\hbox{and}\quad \left(-17, \dfrac{51 \pi}{4} + \pi\right).$

This phenomenon does not occur in rectangular coordinates; it can make things like finding intersection points of polar curves a bit tricky!

You can convert between rectangular and polar using the following conversion formulas:

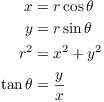
$\eqalign{ x & = r \cos \theta \cr y & = r \sin \theta \cr r^2 & = x^2 + y^2 \cr \noalign{\vskip2 pt} \tan \theta & = \dfrac{y}{x} \cr}$

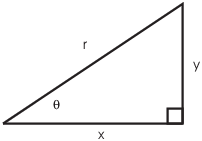
All of them come from the following standard triangle:

$\hbox{\epsfysize=1.25in \epsffile{polar-coordinates-6.eps}}$

Example. Find the polar equation for the circle

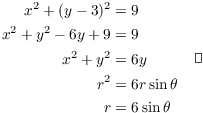
$\eqalign{ x^2 + (y - 3)^2 & = 9 \cr x^2 + y^2 - 6 y + 9 & = 9 \cr x^2 + y^2 & = 6 y \cr r^2 & = 6 r \sin \theta \cr r & = 6 \sin \theta \cr} \quad\halmos$

Example. (a) Find the rectangular equation for the polar curve $r = 4 \cos \theta$ and identify it.

(b) If you start at $\theta = 0$ , how far do you have to go before the graph first closes up?

(a) Multiply by r, substitute , and complete the square:

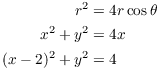
$\eqalign{ r^2 & = 4 r \cos \theta \cr x^2 + y^2 & = 4 x \cr (x - 2)^2 + y^2 & = 4 \cr}$

This is a circle of radius 2 with center at .

(b) The entire circle is traced out as $\theta$ goes from 0 to $\pi$ .

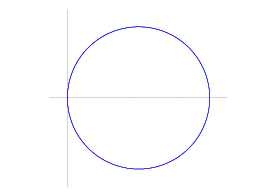
$\hbox{\epsfysize=1.75in \epsffile{polar-coordinates-7.eps}}$

The top half of the circle is traced out from 0 to $\dfrac{\pi}{2}$ . (Draw some radius segments from the origin out to the curve and see.) The bottom half is traced out from $\dfrac{\pi}{2}$ to $\pi$ . It winds up in the fourth quadrant instead of the second because r is negative.

Example. Find the points at which $r^2 = 2 \cos 2 \theta$ and intersect.

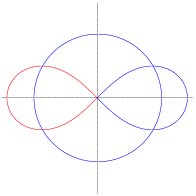
$\hbox{\epsfysize=1.75in \epsffile{polar-coordinates-8.eps}}$

Solve simultaneously:

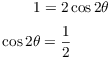
$\eqalign{ 1 & = 2 \cos 2 \theta \cr \noalign{\vskip2 pt} \cos 2 \theta & = \dfrac{1}{2} \cr}$

$\cos 2 \theta$ equals $\dfrac{1}{2}$ when $2 \theta$ is $\dfrac{\pi}{3}$ or $\dfrac{5 \pi}{3}$ . I have to add $2 \pi = \dfrac{6 \pi}{3}$ to get 2 sets of values, since the argument is $2 \theta$ :

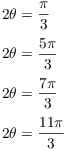
$\eqalign{ 2 \theta & = \dfrac{\pi}{3} \cr \noalign{\vskip2pt} 2 \theta & = \dfrac{5 \pi}{3} \cr \noalign{\vskip2pt} 2 \theta & = \dfrac{7 \pi}{3} \cr \noalign{\vskip2pt} 2 \theta & = \dfrac{11 \pi}{3} \cr}$

Then

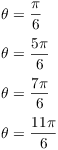
$\eqalign{ \theta & = \dfrac{\pi}{6} \cr \noalign{\vskip2pt} \theta & = \dfrac{5 \pi}{6} \cr \noalign{\vskip2pt} \theta & = \dfrac{7 \pi}{6} \cr \noalign{\vskip2pt} \theta & = \dfrac{11 \pi}{6} \cr}$

Note that there are four intersection points in the picture.

Derivatives in polar coordinates. Here's how to find $\der y x$ for a polar curve. The idea is to use the Chain Rule and the conversion formulas $x = r \cos \theta$ and $y = r \sin \theta$ .

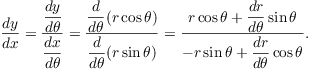
$\der y x = \dfrac{\der y \theta}{\der x \theta} = \dfrac{\der {} \theta (r \cos \theta)}{\der {} \theta (r \sin \theta)} = \dfrac{r \cos \theta + \der r \theta \sin \theta}{-r \sin \theta + \der r \theta \cos \theta}.$

Example. Find the equation of the tangent line to $r = \sin 3 \theta$ at $\theta = \dfrac{\pi}{6}$ .

When $\theta = \dfrac{\pi}{6}$ , . The point of tangency is given by

$x = r \cos \theta = 1 \cdot \cos \dfrac{\pi}{6} = \dfrac{\sqrt{3}}{2}, \quad y = r \sin \theta = 1 \cdot \sin \dfrac{\pi}{6} = \dfrac{1}{2}.$

Now

$\der r \theta = 3 \cos 3 \theta, \quad\hbox{so at}\quad \theta = \dfrac{\pi}{6}, \quad \der r \theta = 0.$

Thus,

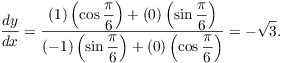
$\der y x = \dfrac{(1)\left(\cos \dfrac{\pi}{6}\right) + (0)\left(\sin \dfrac{\pi}{6}\right)} {(-1)\left(\sin \dfrac{\pi}{6}\right) + (0)\left(\cos \dfrac{\pi}{6}\right)} = -\sqrt{3}.$

The tangent line is

$-\sqrt{3}\left(x - \dfrac{\sqrt{3}}{2}\right) = y - \dfrac{1}{2}.\quad\halmos$

Example. Find $\der y x$ at the point on the polar curve

$r = \dfrac{65}{12} \tan \theta.$

$\hbox{\epsfysize=1.75in \epsffile{polar-coordinates-9.eps}}$

By Pythagoras' theorem, the hypotenuse is . I can also read off

$\sin \theta = \dfrac{12}{13}, \quad \cos \theta = \dfrac{5}{13}.$

Now

$\der r \theta = \dfrac{65}{12} (\sec \theta)^2.$

Since $\sec \theta = \dfrac{13}{5}$ , I have

$\der r \theta = \dfrac{65}{12} \cdot \dfrac{13^2}{5^2} = \dfrac{2197}{60}.$

Then

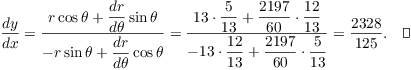
$\der y x = \dfrac{r \cos \theta + \der r \theta \sin \theta}{-r \sin \theta + \der r \theta \cos \theta} = \dfrac{13 \cdot \dfrac{5}{13} + \dfrac{2197}{60} \cdot \dfrac{12}{13}}{-13 \cdot \dfrac{12}{13} + \dfrac{2197}{60} \cdot \dfrac{5}{13}} = \dfrac{2328}{125}.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page