Power Series - Review

Example. Expand $f(x) = \dfrac{5}{11 - x}$ in a power series at and find the interval of convergence.

I will use the series for $\dfrac{1}{1 - u}$ :

$\dfrac{1}{1 - u} = 1 + u + u^2 + \cdots + u^n + \cdots = \sum_{n = 0}^\infty u^n.$

I need powers of , so I make an " " on the bottom, then fix the numbers so the value of the fraction doesn't change. Then I do algebra to put my function into the form $\dfrac{1}{1 - u}$ , at which point I can substitute:

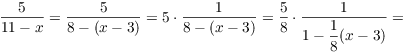
$\dfrac{5}{11 - x} = \dfrac{5}{8 - (x - 3)} = 5 \cdot \dfrac{1}{8 - (x - 3)} = \dfrac{5}{8} \cdot \dfrac{1}{1 - \dfrac{1}{8} (x - 3)} =$

$\dfrac{5}{8} \left(1 + \dfrac{1}{8} (x - 3) + \dfrac{1}{8^2} (x - 3)^2 + \cdot \right) = \dfrac{5}{8} \sum_{n = 0}^\infty \dfrac{1}{8^n} (x - 3)^n.$

I substituted $u = \dfrac{1}{8} (x - 3)$ in the u-series to get my series.

The interval of convergence for the series for $\dfrac{1}{1 - u}$ is . Substitute $u = \dfrac{1}{8} (x - 3)$ :

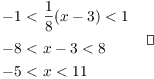
$\eqalign{ -1 <\ & \dfrac{1}{8} (x - 3) < 1 \cr \noalign{\vskip2pt} -8 <\ & x - 3 < 8 \cr -5 <\ & x < 11 \cr} \quad\halmos$

Example. Find the interval of convergence of $\displaystyle \sum_{n=0}^\infty \dfrac{3^n(x - 5)^n}{2^n}$ .

Apply the Root Test:

$\lim_{n \to \infty} \left(\dfrac{3^n|x - 5|^n}{2^n}\right)^{1/n} = \lim_{n \to \infty} \dfrac{3}{2} |x - 5| = \dfrac{3}{2} |x - 5|.$

The series converges for

$\dfrac{3}{2}|x - 5| < 1, \quad\hbox{i.e. for}\quad \dfrac{13}{3} < x < \dfrac{17}{3}.$

At $x = \dfrac{17}{3}$ , the series is

$\sum_{n=0}^\infty \dfrac{3^n}{2^n}\left(\dfrac{17}{3} - 5\right)^n = \sum_{n=0}^\infty 1.$

This series diverges by the Zero Limit Test.

At $x = \dfrac{13}{3}$ , the series is

$\sum_{n=0}^\infty \dfrac{3^n}{2^n}\left(\dfrac{13}{3} - 5\right)^n = \sum_{n=0}^\infty (-1)^n.$

This series also diverges by the Zero Limit Test.

The power series converges for $\dfrac{13}{3} < x < \dfrac{17}{3}$ and diverges elsewhere.

Example. Expand $f(x) = e^{-3 x}$ in a power series at and find the interval of convergence.

$e^{-3 x} = e^{-3(x-4)-12} = e^{-12} e^{-3(x - 4)}.$

Set in

$e^u = 1 + u + \dfrac{u^2}{2!} + \dfrac{u^3}{3!} + \cdots.$

This gives

$e^{-3 x} = e^{-12}\left(1 - 3(x - 4) + \dfrac{3^2(x - 4)^2}{2!} - \dfrac{3^3(x - 4)^3}{3!} + \cdots\right).$

The interval of convergence for the series is $-\infty < u < \infty$ . So for the $e^{-3 x}$ series,

$-\infty < -3(x - 4) < +\infty, \quad -\infty < x < +\infty.\quad\halmos$

Example. Expand $(\cos 5 x)^2$ in a Taylor series at .

Using the double angle formula

$(\cos 5 x)^2 = \dfrac{1}{2}(1 + \cos 10 x) = \dfrac{1}{2} + \dfrac{1}{2}\cos 10 x = \dfrac{1}{2} + \dfrac{1}{2}\left(1 - \dfrac{10^2 x^2}{2!} + \dfrac{10^4 x^4}{4!} - \dfrac{10^6 x^6}{6!} + \cdots\right) =$

$1 - \dfrac{1}{2}\dfrac{10^2 x^2}{2!} + \dfrac{1}{2}\dfrac{10^4 x^4}{4!} - \dfrac{1}{2}\dfrac{10^6 x^6}{6!} + \cdots.\quad\halmos$

Example. (a) Use the first four nonzero terms of the Taylor series for at to approximate $\displaystyle \int_0^1 e^{-x^3}\,dx$ .

(b) Use the Alternating Series Test to estimate the error in part (a).

(a)

$e^{-x^3} = 1 - x^3 + \dfrac{x^6}{2!} - \dfrac{x^9}{3!} + \dfrac{x^{12}}{4!} - \cdots .$

Hence,

$\int_0^1 e^{-x^3}\,dx = \int_0^1 \left(1 - x^3 + \dfrac{x^6}{2!} - \dfrac{x^9}{3!} + \dfrac{x^{12}}{4!} - \cdots\right)\,dx = \left[x - \dfrac{x^4}{4} + \dfrac{x^7}{14} - \dfrac{x^{10}}{60} + \dfrac{x^{13}}{312} - \cdots\right]_0^1 =$

$1 - \dfrac{1}{4} + \dfrac{1}{14} - \dfrac{1}{60} + \dfrac{1}{312} - \cdots \approx 0.80476.$

(I used the first four terms to get the approximation.)

(b) The error is no greater than the next term, which is $\dfrac{1}{312} = 0.00320 \ldots$ .

Example. Use the Taylor series expansion of $\sin x$ at to explain the fact that $\displaystyle \lim_{x \to 0} \dfrac{\sin x}{x} = 1$ .

The series for $\sin x$ at is

$\sin x = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \cdots .$

Divide by x to obtain

$\dfrac{\sin x}{x} = 1 - \dfrac{x^2}{3!} + \dfrac{x^4}{5!} - \cdots.$

Then

$\lim_{x \to 0} \dfrac{\sin x}{x} = \lim_{x \to 0} \left(1 - \dfrac{x^2}{3!} + \dfrac{x^4}{5!} - \cdots\right) = 1.\quad\halmos$

Example. Find the first four nonzero terms of the Taylor expansion for $y = \sin x$ at .

$f'(x) = \cos x, \quad f''(x) = -\sin x, \quad f'''(x) = -\cos x.$

The series is

$\sin x = \sin 3 + (\cos 3)(x - 3) - \dfrac{\sin 3}{2!}(x - 3)^2 - \dfrac{\cos 3}{3!}(x - 3)^3 + \cdots.\quad\halmos$

Example. Find the interval of convergence of $\displaystyle \sum_{n = 1}^\infty \dfrac{(x - 5)^{2 n}}{n\cdot 9^n}$ .

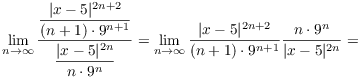
$\lim_{n \to \infty} \dfrac{\dfrac{|x - 5|^{2 n+2}}{(n + 1)\cdot 9^{n+1}}} {\dfrac{|x - 5|^{2 n}}{n\cdot 9^n}} = \lim_{n \to \infty} \dfrac{|x - 5|^{2 n+2}}{(n + 1)\cdot 9^{n+1}} \dfrac{n\cdot 9^n}{|x - 5|^{2 n}} =$

$\lim_{n \to \infty} \dfrac{9^n}{9^{n+1}}\cdot \dfrac{n}{n + 1}\cdot \dfrac{|x - 5|^{2 n+2}}{|x - 5|^{2 n}} = \lim_{n \to \infty} \dfrac{n}{n + 1}\cdot \dfrac{1}{9}|x - 5| = \dfrac{1}{9}|x - 5|^2.$

The series converges for

$\dfrac{1}{9}|x - 5|^2 < 1, \quad\hbox{i.e. for}\quad 2 < x < 8.$

At , the series is

$\sum_{n = 1}^\infty \dfrac{3^{2 n}}{n\cdot 9^n} = \sum_{n = 1}^\infty \dfrac{1}{n}.$

This is harmonic, so it diverges.

At , the series is

$\sum_{n = 1}^\infty \dfrac{(-3)^{2 n}}{n\cdot 9^n} = \sum_{n = 1}^\infty \dfrac{1}{n}.$

This is harmonic, so it diverges.

The power series converges for and diverges elsewhere.

Example. satisfies

$f(2) = 5, \quad f'(2) = 2, \quad f''(2) = -3, \quad f'''(2) = 12.$

Use the third degree Taylor polynomial for f at to approximate .

The third degree Taylor polynomial for f at is

$p_3(x) = 5 + 2(x - 2) - \dfrac{3}{2!}(x - 2)^2 + \dfrac{12}{3!}(x - 2)^3 = 5 + 2(x - 2) - \dfrac{3}{2}(x - 2)^2 + 2(x - 2)^3.$

$f(2.1) \approx p_3(2.1) = 5 + (2)(0.1) - \left(\dfrac{3}{2}\right)(0.1)^2 + 2 \cdot (0.1)^3 = 5.187.\quad\halmos$

Example. Suppose that $f^{(5)}(x) = \dfrac{2}{(1 - x)^7}$ . Use to estimate the error in using the fourth degree Taylor polynomial at to approximate for $0 \le x \le 0.1$ .

For some z between 0 and x,

$R_4(x;0) = \dfrac{f^{(5)}(z)}{5!}x^5 = \dfrac{1}{120}\left(\dfrac{2}{(1 - z)^7}\right) x^5.$

Since $0 \le x \le 0.1$ , $x^5 \le 0.1^5$ .

For the z-term, I have $0 \le z \le x \le 0.1$ . Thus,

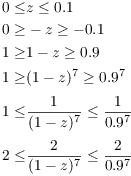
$\eqalign{ 0 \le & z \le 0.1 \cr 0 \ge & -z \ge -0.1 \cr 1 \ge & 1 - z \ge 0.9 \cr 1 \ge & (1 - z)^7 \ge 0.9^7 \cr \noalign{\vskip2pt} 1 \le & \dfrac{1}{(1 - z)^7} \le \dfrac{1}{0.9^7} \cr \noalign{\vskip2pt} 2 \le & \dfrac{2}{(1 - z)^7} \le \dfrac{2}{0.9^7} \cr}$

So $\dfrac{2}{(1 - z)^7} \le \dfrac{2}{0.9^7}$ . Therefore,

$R_4(x;0) \le \left(\dfrac{1}{120}\right)\left(\dfrac{2}{0.9^7}\right)(0.1^5) \approx 3.4845 \cdot 10^{-7}.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page