The Remainder Term

If the Taylor series for a function $f(x)$ is truncated at the $n^{\rm th}$ term, what is the difference between $f(x)$ and the value given by the $n^{\rm th}$ Taylor polynomial? That is, what is the error involved in using the Taylor polynomial to approximate the function?

Theorem. Suppose you expand f around c, and that f is $(n + 1)$ -times continuously differentiable on an open interval containing c. If x is another point in this interval, then for some z in the open interval between x and c,

$$f(x) = \sum_{k = 0}^n \dfrac{f^{(k)}(c)}{k!} (x - c)^k + \dfrac{f^{(n+1)}(z)}{(n + 1)!} (x - c)^{n+1}.$$

$\displaystyle p_n(x; c) = \sum_{k=0}^n \dfrac{f^{(k)}(c)}{k!} (x - c)^k$ is the $n^{\rm th}$ degree Taylor polynomial at c. The other term on the right is called the Lagrange remainder term:

$$R_n(x; c) = \dfrac{f^{(n+1)}(z)}{(n + 1)!} (x - c)^{n+1}.$$

The appearance of z, a point between x and c, and the fact that it's being plugged into a derivative suggest that there is a connection between this result and the Mean Value Theorem. In fact, for $n = 0$ the result says that there is a number z between c and x such that

$$f(x) = f(c) + f'(z)\cdot (x - c).$$

This is the Mean Value Theorem.

On the one hand, this reflects the fact that Taylor's theorem is proved using a generalization of the Mean Value Theorem. On the other hand, this shows that you can regard a Taylor expansion as an extension of the Mean Value Theorem.

Example. Compute the Remainder Term $R_3(x;1)$ for $f(x) = \sin 2 x$ .

For the third remainder term, I need the fourth derivative:

$$f'(x) = 2 \cos 2 x, \quad f''(x) = -4 \sin 2 x, \quad f'''(x) = -8 \cos 2 x, \quad f^{(4)}(x) = 16 \sin 2 x.$$

The Remainder Term is

$$R_3(x; 1) = \dfrac{16 \sin 2 z}{4!}(x - 1)^4.$$

z is a number between x and 1.

Example. Compute the Remainder Term $R_n(x; 3)$ for $f(x) = e^{4 x}$ .

Since I want the $n^{\rm th}$ Remainder Term, I need to find an expression for the $(n + 1)^{\rm st}$ derivative. I'll compute derivative until I see a pattern:

$$f'(x) = 4 e^{4 x}, \quad f''(x) = 4^2 e^{4 x}, \quad f'''(x) = 4^3 e^{4 x}.$$

Notice that it's easier to see the pattern if you don't multiply out the power of 4.

Thus,

$$f^{(n)}(x) = 4^n e^{4 x}, \quad\hbox{so}\quad f^{(n+1)}(x) = 4^{n+1} e^{4 x}.$$

The Remainder Term is

$$R_n(x;3) = \dfrac{4^{n+1} e^{4 z}}{(n + 1)!} (x - 3)^{n+1}.$$

z is a number between x and 3.

There are several things you might do with the Remainder Term:

1. Estimate the error in using $p_n(x; c)$ to estimate $f(x)$ on a given interval $(c - r, c + r)$ . (The interval and the degree n are fixed; you want to find the error.)

2. Find the smallest value of n for which $p_n(x; c)$ approximates $f(x)$ to within a given error ("tolerance") on a given interval $(c - r, c + r)$ . (The interval and the error are fixed; you want to find the degree.)

3. Find the largest interval $(c - r, c + r)$ on which $p_n(x; c)$ approximates $f(x)$ to within a given error ("tolerance"). (The degree and the error are fixed; you want to find the interval.)

Example. The Maclaurin series for $\ln (1 + x)$ is

$$\ln (1 + x) = x - \dfrac{x^2}{2} + \dfrac{x^3}{3} - \dfrac{x^4}{4} + \cdots.$$

What is the largest error which might result from using the first three terms of the series to approximate $\ln (1 + x)$ , if $0 \le x \le 1$ ?

The remainder term is

$$R_n(x;0) = \dfrac{f^{(n+1)}(z)}{(n + 1)!} x^{n+1},$$

I have $0 < z < x$ . I want to estimate the maximum size of $|R_3(x;0)|$ . I take absolute values, because I don't care whether the error is positive or negative, only how large it is.

$f(x) = \ln (1 + x)$ , and you can check by taking derivatives that $f^{(4)}(x) = \dfrac{-6}{(1 + x)^4}$ . Thus, $f^{(4)}(z) = \dfrac{-6}{(1 + z)^4}$ . So

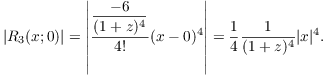
$$|R_3(x;0)| = \left|\dfrac{\dfrac{-6}{(1 + z)^4}}{4!} (x - 0)^4\right| = \dfrac{1}{4} \dfrac{1}{(1 + z)^4} |x|^4.$$

Since I want the largest possible error, I want to see how large the terms $\dfrac{1}{(1 + z)^4}$ and $|x|^4$ could be.

Remember that z is between 0 and x, and $0 \le x \le 1$ . So

$$0 < z < x \le 1.$$

First, $0 \le x \le 1$ means that

$$|x|^4 \le 1^4 = 1.$$

How large can $\dfrac{1}{(1 + z)^4}$ be, given that $0 < z < 1$ ? As z goes from 0 to 1, $\dfrac{1}{(1 + z)^4}$ decreases, so it is largest if $z = 0$ . This means that

$$\dfrac{1}{(1 + z)^4} \le 1.$$

You can also see this by doing the algebra:

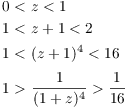
$$\eqalign{ 0 <\ & z < 1 \cr 1 <\ & z + 1 < 2 \cr 1 <\ & (z + 1)^4 < 16 \cr \noalign{\vskip2pt} 1 >\ & \dfrac{1}{(1 + z)^4} > \dfrac{1}{16} \cr}$$

In general, to estimate the z-term you'd have to find the absolute max on the interval for z. If you know that the z-term is either increasing or decreasing, you can check its value at the interval endpoints, and take the largest.

Using the estimates for $\dfrac{1}{(1 + z)^4}$ and $|x|^4$ , I have

$$|R_3(x;0)| \le \dfrac{1}{4} \cdot 1 \cdot 1 = \dfrac{1}{4}.$$

The error is no greater than $\dfrac{1}{4}$ .

I can check this by plotting the difference between the $3^{\rm rd}$ degree Taylor polynomial and $\ln (1 + x)$ .

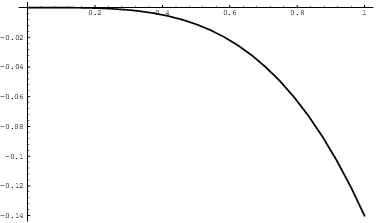
$$\hbox{\epsfysize=2in \epsffile{remainder-term-1.eps}}$$

From the picture, it looks as though the maximum error is around 0.15 (in absolute value). The estimated error was pretty conservative.

Example. (a) Compute $R_3(x;0)$ for $f(x) = \dfrac{1}{2 + x}$ , and express $f(x)$ using $p_3(x)$ and the remainder term.

(b) Use $R_3(x;0)$ to approximate the largest error that occurs in using $p_3(x)$ to approximate $\dfrac{1}{2 + x}$ for $0 \le x \le 1$ .

(a) Since I want $R_3(x;0)$ , I need the fourth derivative:

$$f'(x) = \dfrac{-1}{(2 + x)^2}, \quad f''(x) = \dfrac{2}{(2 + x)^3}, \quad f'''(x) = \dfrac{-6}{(x + x)^4}, \quad f^{(4)}(x) = \dfrac{24}{(2 + x)^5}.$$

Thus,

$$R_3(x;0) = \dfrac{24}{(2 + z)^5} \cdot \dfrac{1}{4!} x^4 = \dfrac{x^4}{(2 + z)^5}.$$

Now

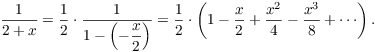
$$\dfrac{1}{2 + x} = \dfrac{1}{2} \cdot \dfrac{1}{1 - \left(-\dfrac{x}{2}\right)} = \dfrac{1}{2} \cdot\left(1 - \dfrac{x}{2} + \dfrac{x^2}{4} - \dfrac{x^3}{8} + \cdots\right).$$

Therefore,

$$\dfrac{1}{2 + x} = \dfrac{1}{2} \cdot\left(1 - \dfrac{x}{2} + \dfrac{x^2}{4} - \dfrac{x^3}{8}\right) + \dfrac{x^4}{(2 + z)^5}.$$

Here z is between 0 and x.

(b) I have

$$|R_3(x;0)| = \dfrac{1}{(2 + z)^5} \cdot |x|^4.$$

I'll estimate the z and x-terms one at a time.

Since $0 \le x \le 1$ , I have

$$|x|^4 \le 1^4 = 1.$$

Since $0 \le x \le 1$ and z is between 0 and x, it follows that $0 \le z \le 1$ . On this interval, $\dfrac{1}{(2 + z)^5}$ decreases, so it attains its largest value at $z = 0$ . Therefore,

$$\dfrac{1}{(2 + z)^5} \le \dfrac{1}{(2 + 0)^5} = \dfrac{1}{32}.$$

Alternatively,

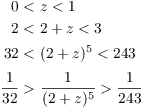
$$\eqalign{ 0 <\ & z < 1 \cr 2 <\ & 2 + z < 3 \cr 32 <\ & (2 + z)^5 < 243 \cr \noalign{\vskip2pt} \dfrac{1}{32} >\ & \dfrac{1}{(2 + z)^5} > \dfrac{1}{243} \cr}$$

Thus,

$$|R_3(x;0)| \le \dfrac{1}{32} \cdot 1 = \dfrac{1}{32}.$$

The error is no greater than $\dfrac{1}{32}$ .

Example. Find the smallest value of n for which the $n^{\rm th}$ degree Taylor series for $f(x) = e^{2 x}$ at $c = 0$ approximates $e^{2 x}$ on the interval $0 \le x \le 0.3$ with an error no greater than $10^{-6}$ .

Notice that

$$f'(x) = 2 e^{2 x}, \quad f''(x) = 2^2 e^{2 x}, \quad f^{(3)}(x) = 2^3 e^{2 x}, \quad \ldots, \quad f^{(n)}(x) = 2^n e^{2 x}.$$

So

$$|R_n(x; 0)| = \left|\dfrac{2^{n+1} e^{2 z}}{(n + 1)!} x^{n+1}\right| = \dfrac{2^{n+1} e^{2 z}}{(n + 1)!} |x|^{n+1} \quad\hbox{for}\quad 0 \le z \le x \le 0.3.$$

First, I'll estimate how large the z and x-terms can be. Since $0 \le x \le 0.3$ and $x^n$ is an increasing function, I have

$$|x|^{n+1} \le 0.3^{n+1}.$$

Since $0 \le z \le 0.3$ and since $e^{2 z}$ is an increasing function, I have

$$e^{2 z} \le e^{0.6}.$$

Thus,

$$|R_n(x; 0)| \le \dfrac{2^{n+1} e^{0.6}}{(n + 1)!} \cdot 0.3^{n + 1} = e^{0.6} \dfrac{0.6^{n + 1}}{(n + 1)!}.$$

Therefore, I want the smallest n for which

$$e^{0.6} \dfrac{0.6^{n + 1}}{(n + 1)!} < 10^{-6}.$$

I can't solve this inequality algebraically, so I'll have to use trial-and-error:

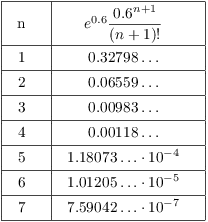
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & n & & $e^{0.6} \dfrac{0.6^{n + 1}}{(n + 1)!}$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 1 & & $0.32798 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 2 & & $0.06559 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 3 & & $0.00983 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 4 & & $0.00118 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 5 & & $1.18073 \ldots \cdot 10^{-4}$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 6 & & $1.01205 \ldots \cdot 10^{-5}$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 7 & & $7.59042 \ldots \cdot 10^{-7}$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

The smallest value of n is $n = 7$ .

You can also use the Remainder Term to estimate the error in using a Taylor polynomial to approximate an integral.

Example. Calvin wants to impress Phoebe Small by using the MacLaurin series for $e^{2 x}$ to approximate $\displaystyle \int_0^{0.5} x e^{2 x}\,dx$ to within 0.0001. How many terms of the series should he use?

The Maclaurin series for $e^{2 x}$ is

$$e^{2 x} = \sum_{n=0}^{\infty} \dfrac{2^n x^n}{n!}.$$

(Substitute $u = 2 x$ in the standard series for $e^u$ .) I want to know how many terms of the series to use to approximate the integral.

Since $f(x) = e^{2 x}$ , I have

$$f'(x) = 2 e^{2 x}, \quad f''(x) = 2^2 e^{2 x}, \ldots f^n(x) = 2^n e^{2 x}.$$

Therefore,

$$R_n(x) = \dfrac{1}{(n + 1)!} f^{(n+1)}(z) (x - c)^{n+1} = \dfrac{1}{(n + 1)!} \cdot 2^n \cdot e^{2 z} \cdot x^{n+1}.$$

In the integral, x goes from 0 to 0.5, and z is a number between 0 (the expansion point) and x. Therefore, I know that z is a number between 0 and 0.5. Taking the worst possible case, the largest $e^{2 c}$ could be is $e^{2 \cdot 0.5} = e$ . Replace $e^{2 z}$ with e to obtain

$$R_n(x) \le \dfrac{1}{(n + 1)!} \cdot 2^n \cdot e \cdot x^{n+1}.$$

Insert this into the integral (remembering to multiply by x):

$$\hbox{error} \le \int_0^{0.5} \dfrac{1}{(n + 1)!} \cdot 2^n \cdot e \cdot x^{n+2}\,dx = \dfrac{1}{(n + 1)!} 2^{n+1} \cdot e \cdot \dfrac{1}{n + 3} \cdot (0.5)^{n+3}.$$

I want the smallest value of n for which this ugly mess is less than 0.0001. The easiest way to do this is by trial: Plug in successive values of n.

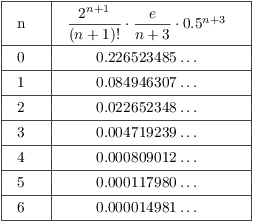
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & n & & $\dfrac{2^{n + 1}}{(n + 1)!} \cdot \dfrac{e}{n + 3} \cdot 0.5^{n + 3}$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 0 & & $0.226523485 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 1 & & $0.084946307 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 2 & & $0.022652348 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 3 & & $0.004719239 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 4 & & $0.000809012 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 5 & & $0.000117980 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 6 & & $0.000014981 \ldots$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

$n = 6$ is the smallest value that works.

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga