Sequences

An sequence is a list of numbers, finite or infinite. Most of what we do will be concerned with infinite sequences.

Here are some sequences:

$$7, 11, 15, 19 \ldots 3 + 4 n, \ldots \quad n \ge 1.$$

$$1, 2, 4, 8, 16, \ldots 2^n, \ldots n \ge 0.$$

The first sequence is an arithmetic sequence: You get the next term by adding a constant (in this case, 4) to the previous term.

The second sequence is a geometric sequence: You get the next term by multiplying the previous term by a constant (in this case, 2). The constant that you multiply by is called the ratio of the geometric sequence.

The expressions $3 + 4 n$ and $2^n$ give the general terms of the sequences, and the ranges for n are given by $n \ge 1$ and $n \ge 0$ . You could write these sequences by just giving their general terms:

$$a_n = 3 + 4 n \quad\hbox{for}\quad n \ge 1.$$

$$b_n = 2^n \quad\hbox{for}\quad n \ge 0.$$

The a and b are just dummy variables. The subscript n is the important thing, since it keeps track of the number of the term and also occurs in the formulas $3 + 4 n$ and $2^n$ .

You can also write $\{3 + 4 n\}_{n = 1}^\infty$ and $\{2^n\}_{n = 0}^\infty$ .

There is no reason why you have to start indexing at 0. Here is the second sequence, indexed from 1:

$$c_n = 2^{n-1}, \quad n = 1, 2, \ldots.$$

The picture below shows a plot of the first few terms of the sequence $b_n = 2^n$ using n on the horizontal axis and the value of the sequence on the vertical axis. That is, I plotted the points

$$(0, 1), (1, 2), (2, 4), (3, 8), (4, 16), \ldots.$$

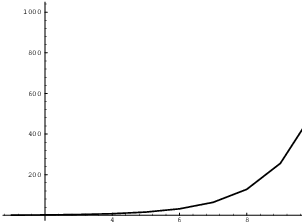
$$\hbox{\epsfysize=2in \epsffile{sequences-1.eps}}$$

To make it look like an ordinary graph, I connected the dots with segments, but you can also plot the points by themselves.

Note that the order of the numbers in a sequence is important. These are different sequences:

$$0, 1, 0, 0, 0, \ldots \quad\hbox{and}\quad 1, 0, 0, 0, 0, \ldots$$

Example. (a) Write the first 5 terms of the arithmetic sequence $b_n = 5 - 2 n$ where $n \ge 0$ .

(b) Write the first 5 terms of the geometric sequence $5 \cdot \left(-\dfrac{1}{3}\right)^n$ where $n \ge 0$ .

(a) The sequence starts with the terms

$$5, 3, 1, -1, -3, \ldots \quad\halmos$$

(b) The sequence starts with the terms

$$5, -\dfrac{5}{3}, \dfrac{5}{9}, -\dfrac{5}{27}, \dfrac{5}{81}, \ldots \quad\halmos$$

We're often concerned with the limit of a sequence --- that is, a number that the terms approach (if there is one). The definition is like the definition of a limit of a function of a real number.

Definition. Let $\{a_n\}$ be a sequence. Then $\displaystyle \lim_{n \to \infty} a_n = L$ means: For every $\epsilon > 0$ , there is a number M such that for $n > M$ ,

$$\epsilon > |a_n - L|.$$

L is called the limit of the sequence. If a sequence has a number as a limit, the sequence converges; otherwise, it diverges.

There are two cases in which we can be more specific about the way that a sequence diverges.

We write $\displaystyle \lim_{n \to \infty} a_n = \infty$ to mean that for every number L, there is a number M such that for $n > M$ ,

$$a_n > L.$$

Likewise, we write $\displaystyle \lim_{n \to \infty} a_n = -\infty$ to mean that for every number L, there is a number M such that for $n > M$ ,

$$a_n < L.$$

Many of the familiar rules for limits of functions hold for limits of sequences.

Theorem. Suppose $\{a_n\}$ , $\{b_n\}$ , and $\{c_n\}$ are sequences. Then:

(a) $\displaystyle \lim_{n \to \infty} k = k$ , where k is a constant.

(b) $\displaystyle \lim_{n \to \infty} (k a_n) = k \cdot \lim_{n \to \infty} a_n$ , where k is a constant.

(c) $\displaystyle \lim_{n \to \infty} (a_n + b_n) = \lim_{n \to \infty} a_n + \lim_{n \to \infty} b_n$ .

(d) $\displaystyle \lim_{n \to \infty} a_n \cdot b_n = \left(\lim_{n \to \infty} a_n\right) \left(\lim_{n \to \infty} b_n\right)$ .

(e) $\displaystyle \lim_{n \to \infty} \dfrac{a_n}{b_n} = \dfrac{\lim_{n \to \infty} a_n}{\lim_{n \to \infty} b_n}$ , provided that $\displaystyle \lim_{n \to \infty} b_n \ne 0$ .

(f) ( Squeezing Theorem) If $a_n \le b_n \le c_n$ for all n, and $\displaystyle \lim_{n \to \infty} a_n = L$ and $\displaystyle \lim_{n \to \infty} c_n = L$ , then $\displaystyle \lim_{n \to \infty} b_n = L$ .

As usual, in parts (b), (c), (d), and (e) the interpretation is that the two sides of an equation are equal when all the limits involved are defined.

Besides the rules above, you may also use L'H\^opital's Rule to compute limits of sequences.

Proof. I'll prove (c) as an example. Suppose

$$\lim_{n \to \infty} a_n = p \quad\hbox{and}\quad \lim_{n \to \infty} b_n = q.$$

I'll prove that

$$\lim_{n \to \infty} (a_n + b_n) = p + q.$$

Let $\epsilon > 0$ . Choose a number L so that if $n > L$ , then

$$\dfrac{\epsilon}{2} > |a_n - p|.$$

Choose a number M so that if $n > M$ , then

$$\dfrac{\epsilon}{2} > |b_n - q|.$$

Then let $N = \max(L, M)$ , so N is the larger of L and M. Then if $n > N$ , I have both

$$\dfrac{\epsilon}{2} > |a_n - p| \quad\hbox{and}\quad \dfrac{\epsilon}{2} > |b_n - q|.$$

I add the inequalities and use the Triangle Inequality:

$$\eqalign{ \epsilon = \dfrac{\epsilon}{2} + \dfrac{\epsilon}{2} & > |a_n - p| + |b_n - q| \cr & \ge |(a_n - p) + (b_n - q)| \cr & = |(a_n + b_n) - (p + q)| \cr}$$

This proves that $\displaystyle \lim_{n \to \infty} (a_n + b_n) = p + q$ .

The limit of a geometric sequence is determined entirely by its ratio r. The following result describes the cases.

Proposition. Let $\{a r^n\}$ be a geometric sequence.

(a) If $r > 1$ , then $a r^n \to +\infty$ if $a > 0$ , $a r^n \to -\infty$ if $a < 0$ , and $a r^n \to 0$ if $a = 0$ .

(b) If $r < -1$ , then $a r^n$ diverges to $\pm \infty$ by oscillation.

(c) If $r = 1$ , then $a r^n = a$ for all n, and $a_n \to 1$ .

(d) If $r = -1$ , then $a r^n$ diverges to $\pm a$ by oscillation.

(e) If $|r| < 1$ , then $a r^n \to 0$ .

Proof. I'll sketch a proof that $r^n \to 0$ if $0 < r < 1$ to illustrate the ideas.

Note that since $r < 1$ ,

$$r^{n + 1} < r^n.$$

That is, the sequence $\{r^n\}$ decreases. The terms are all positive, so they're bounded below by 0. As we'll see below, a decreasing sequence that is bounded below must have a limit. So $\displaystyle \lim_{n \to \infty} r^n$ is defined.

Now

$$\lim_{n \to \infty} r^n = \lim_{n \to \infty} r \cdot r^{n - 1} = r \lim_{n \to \infty} r^{n - 1}.$$

But

$$\lim_{n \to \infty} r^n = \lim_{n \to \infty} r^{n - 1}.$$

Call this common limit L. Then the last equation says

$$L = r \cdot L.$$

Since $r \ne 0$ , this implies that $L = 0$ .

Here are some examples to illustrate the cases:

$$r > 1:\ 2, 4, 8, 16, \ldots \to \infty.$$

$$r < -1:\ -3, 9, -27, 81, -243 \to \pm \infty.$$

$$r = 1:\ 7, 7, 7, 7, 7, \ldots \to 7.$$

$$r = -1:\ 5, -5, 5, -5, 5, \ldots \to \pm 5.$$

$$r = \dfrac{2}{3}:\ \dfrac{2}{3}, \dfrac{4}{9}, \dfrac{8}{27}, \dfrac{16}{81}, \dfrac{32}{243}, \ldots \to 0.$$

Here is a geometric sequence in which each term is $\dfrac{1}{2}$ times the previous term:

$$1, \quad \dfrac{1}{2}, \quad \dfrac{1}{4}, \quad \dfrac{1}{8}, \ldots, \dfrac{1}{2^n}, \ldots.$$

The terms appear to approach 0, so $\displaystyle \lim_{n \to \infty} \dfrac{1}{2^n} = 0$ .

Here is a picture of the terms in this sequence.

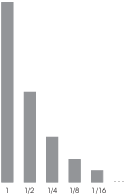
$$\hbox{\epsfysize=1.75 in \epsffile{sequences-2.eps}}$$

Notice that the rectangles' heights approach 0.

Here is a geometric sequence in which each term is $\dfrac{4}{3}$ times the previous term:

$$1, \quad \dfrac{4}{3}, \quad \dfrac{16}{9}, \quad \dfrac{64}{27}, \ldots, \dfrac{4^n}{3^n}, \ldots.$$

The terms appear to increase indefinitely, so I'll write $\displaystyle \lim_{n \to \infty} \dfrac{4^n}{3^n} = \infty$ .

Here is an interesting way to picture of the terms in this sequence. Take a segment and divide it into thirds. Replace the middle third with a "bump" shaped like an equilateral triangle.

$$\hbox{\epsfysize=1.25 in \epsffile{sequences-3.eps}}$$

If the original segment had length 1, the new path with the triangular bump has length $\dfrac{4}{3}$ .

Now repeat the process with each of the four segments:

$$\hbox{\epsfysize=1.25 in \epsffile{sequences-4.eps}}$$

Since each segment's length is multiplied by $\dfrac{4}{3}$ , this path has total length $\left(\dfrac{4}{3}\right)^2 = \dfrac{16}{9}$ .

Here's the result of repeating the process two more times:

$$\hbox{\epsfysize=1.25 in \epsffile{sequences-5.eps}}$$

If you continue this process indefinitely, the limiting path must have infinite length, since $\displaystyle \lim_{n \to \infty} \dfrac{4^n}{3^n} = \infty$ . The limiting path is an example of a self-similar fractal.

Example. Determine whether the sequence $a_n = \dfrac{2 n^2 - 3 n + 1}{5 - 7 n^2}$ for $n \ge 1$ converges or diverges. If it converges, find the limit.

$$\lim_{n \to \infty} \dfrac{2 n^2 - 3 n + 1}{5 - 7 n^2} = \lim_{n \to \infty} \dfrac{4 n - 3}{-14 n} = \lim_{n \to \infty} \dfrac{4}{-14} = -\dfrac{2}{7}.$$

Hence, the series converges.

Example. Determine whether the sequence $a_n = \dfrac{2^n + 7}{5^n - 3}$ for $n \ge 1$ converges or diverges. If it converges, find the limit.

Divide the top and bottom by $5^n$ :

$$\lim_{n \to \infty} \dfrac{2^n + 7}{5^n - 3} = \lim_{n \to \infty} \dfrac{\dfrac{2^n}{5^n} + \dfrac{7}{5^n}}{1 - \dfrac{3}{5^n}}.$$

Now $\dfrac{2^n}{5^n} = \left(\dfrac{2}{5}\right)^n$ , and this goes to 0 because $\dfrac{2}{5} < 1$ . Clearly $\dfrac{7}{5^n}$ and $\dfrac{3}{5^n}$ go to 0. The limit reduces to

$$\lim_{n \to \infty} \dfrac{\dfrac{2^n}{5^n} + \dfrac{7}{5^n}}{1 - \dfrac{3}{5^n}} = \dfrac{0 + 0}{1 - 0} = 0.$$

The sequence converges to 0.

Example. (a) Determine whether the sequence $a_n = (-1)^n\dfrac{n}{n^2 + 1}$ for $n \ge 1$ converges or diverges. If it converges, find the limit.

(b) Determine whether the sequence $a_n = (-1)^n \dfrac{n}{n + 1}$ for $n \ge 1$ converges or diverges. If it converges, find the limit.

(a) Since $(-1)^n = \pm 1$ , I have

$$-\dfrac{n}{n^2 + 1} \le (-1)^n\dfrac{n}{n^2 + 1} \le \dfrac{n}{n^2 + 1}.$$

Now

$$\lim_{n \to \infty} -\dfrac{n}{n^2 + 1} = 0 \quad\hbox{and}\quad \lim_{n \to \infty} \dfrac{n}{n^2 + 1} = 0.$$

By the Squeezing Theorem,

$$\lim_{n \to \infty} (-1)^n\dfrac{n}{n^2 + 1} = 0.\quad\halmos$$

(b) Note that

$$\lim_{n \to \infty} \dfrac{n}{n + 1} = 1.$$

Hence, when n is large and even, $(-1)^n\dfrac{n}{n + 1}$ is close to 1, and when n is large and odd, $(-1)^n\dfrac{n}{n + 1}$ is close to -1. Therefore, the sequence diverges by oscillation.

Example. Determine whether the sequence $a_n = \dfrac{(\sin n)^2}{n}$ converges or diverges. If it converges, find the limit.

Note that

$$-1 \le \sin n \le 1, \quad\hbox{so}\quad 0 \le (\sin n)^2 \le 1.$$

(The "$0 \le$ " comes from the fact that squares can't be negative.) Divide by n:

$$0 \le \dfrac{(\sin n)^2}{n} \le \dfrac{1}{n}.$$

Now $\displaystyle \lim_{n \to \infty} 0 = 0$ and $\displaystyle \lim_{n \to \infty} \dfrac{1}{n} = 0$ , so by the Squeezing Theorem,

$$\lim_{n \to \infty} \dfrac{(\sin n)^2}{n} = 0.$$

The sequence converges to 0.

Example. A sequence defined by recursion:

$$a_0 = 1, \quad a_{n+1} = \sqrt{12 + a_n}, \quad n \ge 1.$$

Here are the first few terms:

$$1, \sqrt{13}, \sqrt{12 + \sqrt{13}}, \sqrt{12 + \sqrt{12 + \sqrt{13}}}.$$

Assume that $\displaystyle \lim_{n \to \infty} a_n$ exists. What is it?

Let $\displaystyle L = \lim_{n \to \infty} a_n$ . Then

$$\lim_{n \to \infty} a_n = L = \lim_{n \to \infty} a_{n+1}.$$

They're equal because both represent the limit of sequences of terms with the "same infinite part".

So

$$\lim_{n \to \infty} a_{n+1} = \lim_{n \to \infty} \sqrt{12 + a_n} = \sqrt{12 + \lim_{n \to \infty} a_n}.$$

Substitute L and solve the resulting equation:

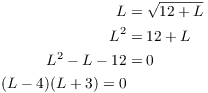
$$\eqalign{ L & = \sqrt{12 + L} \cr L^2 & = 12 + L \cr L^2 - L - 12 & = 0 \cr (L - 4)(L + 3) = 0 \cr}$$

This gives the solutions $L = 4$ and $L = -3$ . Since its clear from the definition of the sequence that the sequence has positive terms, the limit can't be negative. Hence, $L = 4$ .

Example. Start with a positive integer. If it is even, divide it by 2. If it is odd, multiply by 3 and add 1. Continue forever. You obtain a sequence of numbers --- a different sequence for each number you start with.

Show that the sequence of numbers produced by this procedure starting at 23 eventually leads to the terms 4, 2, 1, which repeat after this.

$$23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, \ldots$$

For example, 23 is odd, so the next number is $3 \cdot 23 + 1 = 70$ . Then 70 is even, so the next number is $\dfrac{70}{2} = 35$ .

If you try other starting numbers, you'll find that you always seem to get stuck in the $1-2-4$ loop. The Collatz conjecture says that this always happens. It is known to be true for starting numbers (at least) up to $3 \times 10^{12}$ .

Definition. A sequence $\{a_n\}$ :

(a) Increases if $a_i < a_j$ whenever $i < j$ .

(b) Decreases if $a_i > a_j$ whenever $i < j$ .

You can treat the terms of a sequence as values of a continuous function and use the first derivative to determine whether a sequence increases or decreases.

Example. Determine whether the sequence given by $a_n = \dfrac{n + 1}{n + 3}$ increases, decreases, or does neither.

Set $f(x) = \dfrac{x + 1}{x + 3}$ . Then

$$f'(x) = \dfrac{(x + 3)(1) - (x + 1)(1)}{(x + 3)^2} = \dfrac{2}{(x + 3)^2}.$$

Since $f'(x) > 0$ for all x, the sequence increases.

In some cases, it's not possible to use the derivative to determine whether a sequence increases or decreases. Here's another approach that is often useful:

Proposition. Let $\{a_n\}$ be a sequence with positive terms, and suppose that $\displaystyle \lim_{n \to \infty} \dfrac{a_{n+1}}{a_n} = L$ . Then:

(a) If $L < 1$ , the terms eventually decrease.

(b) If $L > 1$ , the terms eventually increase.

Proof. Here's a sketch of the proof of (a). Suppose $\displaystyle \lim_{n \to \infty} \dfrac{a_{n+1}}{a_n} = L < 1$ . Choose a number r such that $L < r < 1$ . Then there is a number M such that if $n > M$ ,

$$\dfrac{a_{n+1}}{a_n} < r < 1, \quad\hbox{so}\quad a_{n+1} < a_n.$$

The last inequality says that the next term ($a_{n+1}$ ) is less than the current term ($a_n$ ), which means that the terms decrease. Similar reasoning applies if $L > 1$ .

The reason I have to say the terms eventually decrease or increase is that the limit tells what the sequence does for large values of n. For small values of n, the sequence may increase or decrease, and this behavior won't be detected by taking the limit.

Example. Determine whether the sequence given by $a_n = \dfrac{4^n}{n!}$ increases, decreases, or does neither.

I compute $\displaystyle \lim_{n \to \infty} \dfrac{a_{n+1}}{a_n}$ :

$$\lim_{n \to \infty} \dfrac{a_{n+1}}{a_n} = \lim_{n \to \infty} \dfrac{\dfrac{4^{n+1}}{(n + 1)!}} {\dfrac{4^n}{n!}} = \lim_{n \to \infty} \dfrac{4^{n+1}}{(n + 1)!}\cdot \dfrac{n!}{4^n} = \lim_{n \to \infty} \dfrac{4^{n+1}}{4^n}\cdot \dfrac{n!}{(n + 1)!} =$$

$$\lim_{n \to \infty} 4\cdot \dfrac{1\cdot 2\cdot \cdots \cdot n} {1\cdot 2\cdot \cdots \cdot n\cdot (n + 1)} = \lim_{n \to \infty} 4\cdot \dfrac{1}{n + 1} = 0.$$

Since is limit is less than 1, the terms of the sequence eventually decrease.

Definition. A sequence $\{a_n\}$ is bounded if there is a number M such that $|a_n| \le M$ for all n.

Pictorially, this means that all of the terms of the sequence lie between the lines $y = -M$ and $y = M$ :

$$\hbox{\epsfysize=1.75 in \epsffile{sequences-6.eps}}$$

I can also say a sequence is bounded if there are numbers C and D such that $C \le a_n \le D$ for all n. This definition is equivalent to the first definition. For if a sequence satisfies $|a_n| \le M$ for all n, then $-M \le a_n \le M$ for all n (so I can take $C = -M$ and $D = M$ in the second definition). On the other hand, if $C \le a_n \le D$ for all n, then $|a_n| \le \max(|C|, |D|)$ , where $\max(|C|, |D|)$ is the larger of the numbers $|C|$ and $|D|$ (so I can take $M = \max(|C|, |D|)$ in the first definition).

Example. Prove that the sequence $a_n = 5 + 2 \sin n$ is bounded.

Since $-1 \le \sin n \le 1$ ,

$$-2 \le 2 \sin n \le 2, \quad\hbox{so}\quad 3 \le 5 + 2 \sin n \le 7.$$

Thus, the sequence is bounded according to the second definition. Also, $-7 \le 5 + 2 \sin n \le 7$ , and hence $|5 + 2 \sin n| \le 7$ . Therefore, the sequence is bounded according to the first definition.

Here's another way of telling that a sequence is bounded:

Proposition. If the terms of a sequence approach a (finite) limit, then the sequence is bounded.

Proof. Suppose that $\displaystyle \lim_{n \to \infty} a_n = L$ . By definition, this means that I can make $a_n$ as close to L as I want by making n large enough. Suppose, for instance, I know that $a_n$ is within 0.1 of L once n is greater than some number p. (I picked the number 0.1 at random.) Thus, all the terms after $a_p$ are within 0.1 of L:

$$L - 0.1 < a_{p+1}, a_{p+2}, \ldots < L + 0.1.$$

What about the first p terms $a_1$ , $a_2$ , ..., $a_p$ ? Since there are a finite number of these terms, there must be a largest value and a smallest value among them. Suppose that the smallest value is A and the largest value is B. Thus,

$$A \le a_1, a_2, \ldots, a_p \le B.$$

Then if $C = \min(A, L - 0.1)$ is the smaller of A and $L - 0.1$ and $D = \max(B, L + 0.1)$ is the larger of B and $L + 0.1$ , I must have

$$C \le a_1, a_2, \ldots, a_p, a_{p+1}, a_{p+2}, \ldots D.$$

Therefore, the sequence is bounded.

Example. Prove that the sequence $a_n = \dfrac{4 n^2}{8 n^2 + 3}$ is bounded.

$$\lim_{n \to \infty} \dfrac{4 n^2}{8 n^2 + 3} = \dfrac{1}{2}.$$

Therefore, the sequence is bounded.

There is an important theorem which combines the ideas of increasing or decreasing and boundedness. It says that an increasing sequence that is bounded above has a limit, and a decreasing sequence that is bounded below has a limit.

Some of the material which leads up to this result is a bit technical, so you might want to skip the proofs if you find them heavy-going. The important thing is the last theorem in this section, which we'll often use in our discussion of infinite series.

Definition. Let S be a set of real numbers.

(a) An upper bound for S is a number M such that $M \ge x$ for every number x in S. A set which has an upper bound is bounded above.

(b) A lower bound for S is a number L such that $L \le x$ for every number x in S. A set which has a lower bound is bounded below.

A sequence is bounded in the sense we discussed earlier if it's bounded above and bounded below.

For instance, consider the set

$$S = \left\{\dfrac{1}{2}, \dfrac{1}{4}, \dfrac{1}{8}, \ldots \dfrac{1}{2^n}, \ldots\right\}.$$

Then 1 is an upper bound for S. So is 2. So is $\pi$ . There are infinitely many upper bounds for S.

0 is a lower bound for S. So is -17. There are infinitely many lower bounds for S.

Thus, a set can have many upper bounds or lower bounds.

Consider the set

$$S = \{1, 2, 3, 4, \ldots n, \ldots \}.$$

S does not have an upper bound: There's no number which is greater than or equal to all the numbers in S. But 0 is a lower bound for S. So is -151.

Thus, a set does not have to have an upper bound or a lower bound.

Definition. Let S be a set.

(a) A number M is the least upper bound for S if M is an upper bound for S, and $M \le M'$ for every upper bound $M'$ of S.

(b) A number L is the greatest lower bound for S if L is an lower bound for S, and $L' \le L$ for every lower bound $L'$ of S.

We've seen that a set can have many upper bounds. The least upper bound is the smallest upper bound.

$$\hbox{\epsfysize=1.5in \epsffile{sequences-7.eps}}$$

Let's consider again the set

$$S = \left\{\dfrac{1}{2}, \dfrac{1}{4}, \dfrac{1}{8}, \ldots \dfrac{1}{2^n}, \ldots\right\}.$$

We saw that 1, 2, and $\pi$ are upper bounds for S. The least upper bound is $\dfrac{1}{2}$ . In this case, the least upper bound is an element of the set.

Consider the set

$$T = \left\{\dfrac{1}{2}, \dfrac{2}{3}, \dfrac{3}{4}, \ldots \dfrac{n}{n + 1}, \ldots\right\}.$$

Notice that $\displaystyle \lim_{n \to \infty} \dfrac{n}{n + 1} = 1$ . The least upper bound of the set T is 1. It is not an element of T.

We've already seen an example of a set with no upper bound:

$$S = \{1, 2, 3, 4, \ldots n, \ldots \}.$$

Since this set has no upper bound, it can't have a least upper bound. There is an important circumstance when a set is guaranteed to have a least upper bound.

Axiom. ( Least Upper Bound Axiom) Let S be a nonempty set of real numbers that is bounded above. Then S has a least upper bound.

This is an axiom for the real numbers: that is, one of the assumptions which characterize the real numbers. Being an assumption, there's no question of proving it. You'd see the axioms for the real numbers in a course in analysis.

For a course in calculus, the following result is one of the most important consequences of this axiom. It will be used in our discussion of infinite series.

Theorem. (a) A sequence of numbers that increases and is bounded above has a limit.

(b) A sequence of numbers that decreases and is bounded below has a limit.

The following picture makes the theorem plausible:

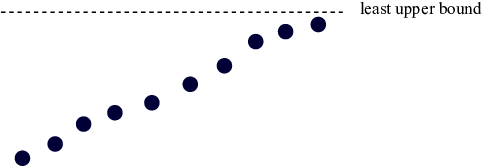
$$\hbox{\epsfysize=1.5in \epsffile{sequences-8.eps}}$$

Since the sequence is bounded above, it has a least upper bound. It appear that, since the terms increase, they should "pile up" at the least upper bound, and therefore have a limit.

Proof. I'll sketch the proof of (a) by way of example.

Suppose $\{a_n\}_{n = 1}^\infty$ is an increasing sequence, and suppose that it's bounded above. Since it's bounded above, the Least Upper Bound Axiom implies that it has an upper bound M. I will show that

$$\lim_{n \to \infty} a_n = M.$$

Let $\epsilon > 0$ , and consider the number $M - \epsilon$ . Suppose

$$a_n \le M - \epsilon \quad\hbox{for all}\quad n.$$

Tthen $M - \epsilon$ is an upper bound for $\{a_n\}$ . But $M - \epsilon < M$ , and M is supposed to be the smallest upper bound for $\{a_n\}$ . This is impossible. Hence, I can't have $a_n \le M - \epsilon$ for all n.

This means that for some index k I have $a_k > M - \epsilon$ . The the sequence increases, so

$$\cdots a_{k + 3} > a_{k + 2} > a_{k + 1} > a_k > M - \epsilon.$$

In other words, $a_n > M - \epsilon$ for all $n \ge k$ .

By the definition of the limit of a sequence, I have $\displaystyle \lim_{n \to \infty} a_n = M$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga