Infinite Series

An infinite series is a sum

$$a_0 + a_1 + a_2 + \cdots + a_n + \cdots .$$

I can use summation notation if I don't want to write the terms out:

$$\sum_{k = 0}^\infty a_k = a_0 + a_1 + a_2 + \cdots + a_n + \cdots .$$

For example,

$$\sum_{k = 0}^\infty (-1)^k = 1 - 1 + 1 - 1 + 1 - \cdots + (-1)^n + \cdots,$$

$$\sum_{k = 0}^\infty \dfrac{1}{2^k} = 1 + \dfrac{1}{2} + \dfrac{1}{4} + \cdots + \dfrac{1}{2^n} + \cdots,$$

$$\sum_{k=1}^\infty \dfrac{1}{k} = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{n} + \cdots.$$

Addition is not defined for an infinite collection of numbers. I have to define what I mean by the sum of an infinite series like those above. To do this, I'll look at the sequence of partial sums. For $a_0 + a_1 + a_2 + \cdots + a_n + \cdots$ , the partial sums are

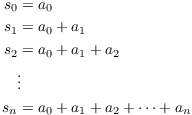
$$\eqalign{ s_0 & = a_0 \cr s_1 & = a_0 + a_1 \cr s_2 & = a_0 + a_1 + a_2 \cr & \vdots \cr s_n & = a_0 + a_1 + a_2 + \cdots + a_n \cr}$$

To say that the sum of the series is S means that the sequence of partial sums converges to S:

$$\lim_{n \to \infty} s_n = S.$$

The notation for this is

$$\sum_{k = 0}^\infty a_k = S.$$

It is often difficult to compute the sum of an infinite series exactly. However, you can often tell that a series converges without knowing what it converges to. If necessary, a computer can be used to approximate the sum of a convergent series.

Some infinite series are already familiar to you. For example, the decimal representation of a real number is a convergent infinite series. Here is the number $\pi$ :

$$3.14159265 \ldots 3 + \dfrac{1}{10} + \dfrac{4}{100} + \dfrac{1}{1000} + \dfrac{5}{10000} + \cdots .$$

It's an infinite non-repeating decimal.

Repeating decimals represent rational numbers. I'll show by example how to convert a repeating decimal to a rational fraction. Consider $0.272727 \ldots$ . Set $x = 0.272727 \ldots$ . Then

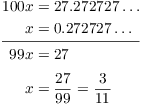
$$\eqalign{ 100 x & = 27.272727 \ldots \cr x & = 0.272727 \ldots \cr \noalign{\vskip2pt \hrule \vskip2pt} 99 x & = 27 \cr \noalign{\vskip2pt} x & = \dfrac{27}{99} = \dfrac{3}{11} \cr}$$

Definition. A geometric series is a series of the form

$$a + a r + a r^2 + a r^3 + \cdots + a r^n + \cdots = \sum_{k = 0}^\infty ar^k.$$

The picture below shows the partial sums of the geometric series

$$1 + \dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8} + \cdots.$$

Notice that the partial sums seem to approach 2.

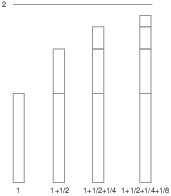
$$\hbox{\epsfysize=1.75 in \epsffile{series-1.eps}}$$

To find a formula for the sum of a geometric series, I'll start by computing the $n^{\rm th}$ partial sum. By long division,

$$\dfrac{1}{1 - r} = 1 + r + r^2 + \cdots + r^n + \dfrac{r^{n+1}}{1 - r}.$$

(This will make sense provided that $r \ne 1$ .)

Multiply by a, then move the last term on the right to the left:

$$\sum_{k = 0}^n a r^k = a + a r + a r^2 + a r^3 + \cdots + a r^n = \dfrac{a}{1 - r} - \dfrac{a r^{n+1}}{1 - r} = \dfrac{a - a r^{n + 1}}{1 - r}.$$

This gives a formula for the sum of a finite geometric series.

For instance,

$$3 + 3\cdot 5 + 3\cdot 5^2 + \cdots + 3\cdot 5^{100} = \dfrac{3}{1 - 5} - \dfrac{3\cdot 5^{101}}{1 - 5} = \dfrac{3}{4} \left(5^{101} - 1\right).$$

What about the infinite series

$$\sum_{k = 0}^\infty a r^k = a + a r + a r^2 + a r^3 + \cdots + a r^n + \cdots?$$

The series converges if the limit of $n^{\rm th}$ partial sum exists. I need to compute

$$\lim_{n \to \infty} \left(\dfrac{a}{1 - r} - \dfrac{ar^{n+1}}{1 - r}\right) = \dfrac{a}{1 - r} - \dfrac{a}{1 - r} \lim_{n \to \infty} r^{n+1}.$$

By a result on geometric sequences,

$$\lim_{n \to \infty} r^{n+1} = \cases{ 0 & if $|r| < 1$ \cr \hbox{diverges} & if $|r| \ge 1$ \cr}.$$

Hence,

$$\sum_{k = 0}^\infty a r^k = \cases{ \dfrac{a}{1 - r} & if $|r| < 1$ \cr \hbox{diverges} & if $|r| \ge 1$ \cr}.$$

For instance,

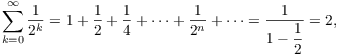
$$\sum_{k = 0}^\infty \dfrac{1}{2^k} = 1 + \dfrac{1}{2} + \dfrac{1}{4} + \cdots + \dfrac{1}{2^n} + \cdots = \dfrac{1}{1 - \dfrac{1}{2}} = 2,$$

$$\sum_{k = 0}^\infty 3 \cdot 5^k = 3 + 3 \cdot 5 + 3 \cdot 5^2 + \cdots + 3 \cdot 5^n + \cdots\ \hbox{diverges}.$$

What about something like

$$\sum_{k = 5}^\infty 4 \cdot \left(-\dfrac{1}{3}\right)^k = 4 \cdot \left(-\dfrac{1}{3}\right)^5 + 4 \cdot \left(-\dfrac{1}{3}\right)^6 + 4 \cdot \left(-\dfrac{1}{3}\right)^7 + \cdots ?$$

Well, this is

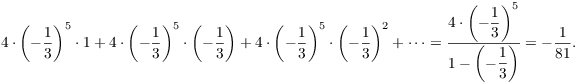
$$4 \cdot \left(-\dfrac{1}{3}\right)^5 \cdot 1 + 4 \cdot \left(-\dfrac{1}{3}\right)^5 \cdot \left(-\dfrac{1}{3}\right) + 4 \cdot \left(-\dfrac{1}{3}\right)^5 \cdot \left(-\dfrac{1}{3}\right)^2 + \cdots = \dfrac{4\cdot \left(-\dfrac{1}{3}\right)^5}{1 - \left(-\dfrac{1}{3}\right)} = -\dfrac{1}{81}.$$

Example. (Retirement) $200 is deposited each month and collects $4.8%$ annual interest, compounded monthly. How much is in the account after 30 years?

Note that 30 years is 360 months.

$4.8%$ annual interest, compounded monthly, means that each month the amount in the account earns $\dfrac{4.8%}{12} = 0.4%$ interest. This means that the amount in the account is multiplied by 1.004 each month.

The table below tracks each monthly deposit. The first row represents the first $200 deposited, the second row the second $200 deposited, and so on.

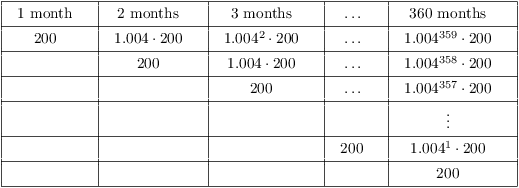
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 month & & 2 months & & 3 months & & \dots & & 360 months & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 200 & & $1.004\cdot 200$ & & $1.004^2\cdot 200$ & & \dots & & $1.004^{359}\cdot 200$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & 200 & & $1.004\cdot 200$ & & \dots & & $1.004^{358}\cdot 200$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & & & 200 & & \dots & & $1.004^{357}\cdot 200$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & & & & & & & $\vdots$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & & & & & 200 & & $1.004^1\cdot 200$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & & & & & & & 200 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The total amount in the account is the sum of the numbers in the last column, which is

$$200 \cdot \sum_{n=0}^{359} 1.004^n = 200 \cdot \dfrac{1 - 1.004^{360}}{1 - 1.004} \approx 160429.$$

By comparison, with no interest --- e.g. if you put $200 a month under your mattress --- you'd only have $72000 after 30 years.

At the same time, this is a rather sobering conclusion. Many people would find it a challenge to put away $200 a month toward retirement. This problem shows that doing so and assuming a moderate interest rate produces a significant total --- but definitely not enough to retire on!

The harmonic series is the series

$$\sum_{k = 1}^\infty \dfrac{1}{k} = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{n} + \cdots .$$

It is an important example of a divergent series.

Here's an easy way to convince yourself that it diverges. Write down the terms of the series, and underneath the terms of a new series. The terms of the new series are all less than or equal to the terms of the harmonic series:

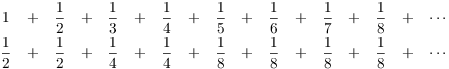
$$\matrix{ 1 & + & \dfrac{1}{2} & + & \dfrac{1}{3} & + & \dfrac{1}{4} & + & \dfrac{1}{5} & + & \dfrac{1}{6} & + & \dfrac{1}{7} & + & \dfrac{1}{8} & + & \cdots \cr \noalign{\vskip2pt} \dfrac{1}{2} & + & \dfrac{1}{2} & + & \dfrac{1}{4} & + & \dfrac{1}{4} & + & \dfrac{1}{8} & + & \dfrac{1}{8} & + & \dfrac{1}{8} & + & \dfrac{1}{8} & + & \cdots \cr}$$

Do you see the pattern? Next, you'll take the 8 terms of the harmonic series from $\dfrac{1}{9}$ to $\dfrac{1}{16}$ and write $\dfrac{1}{16}$ under each of them, then the next 16 terms of the harmonic series, and so on.

Consider the series on the bottom. The first two terms are both $\dfrac{1}{2}$ . After that, the sum of the next two terms is is $\dfrac{1}{4} + \dfrac{1}{4} = \dfrac{1}{2}$ . After that, the sum of the next four terms is

$$\dfrac{1}{8} + \dfrac{1}{8} + \dfrac{1}{8} + \dfrac{1}{8} = \dfrac{1}{2}.$$

And so on. So the series on the bottom is an infinite sum of $\dfrac{1}{2}$ 's, which goes to infinity. Since term-by-term the harmonic series is at least as big, it must diverge to infinity as well.

The harmonic series is a member of a family of series called p-series. Here the the facts about convergence and divergence of p-series.

Proposition. Let $\displaystyle \sum_{n = 1}^\infty \dfrac{1}{n^p}$ be a p-series, where $p > 0$ .

(a) If $p > 1$ , the series converges.

(b) If $0 < p < 1$ , the series diverges.

The harmonic series is the case $p = 1$ . For example,

$$\sum_{k = 1}^\infty \dfrac{1}{k^3} \quad\hbox{converges},$$

$$\sum_{k = 1}^\infty \dfrac{1}{\sqrt{k}} \quad\hbox{diverges},$$

$$\sum_{k = 1}^\infty k^{-3/4} \quad\hbox{diverges}.$$

I'll prove the result above using the Integral Test, which I'll discuss later.

If $p > 1$ , the sum of the p-series is denoted $\zeta(p)$ . Thus,

$$\zeta(3) = \sum_{k = 1}^\infty \dfrac{1}{k^3}.$$

It isn't too difficult to find closed form expressions for $\zeta(2 n)$ , where n is an integer. For instance,

$$\zeta(2) = \sum_{k = 1}^\infty \dfrac{1}{k^2} = \dfrac{\pi^2}{6}.$$

However, the odd sums $\zeta(2 n + 1)$ are somewhat mysterious. It was only in 1978 that R. Ap\'ery showed that $\zeta(3)$ is irrational. No one knows what its exact value is, and no one knows if (for instance) $\zeta(5)$ is irrational.

Here are some properties of convergent and divergent series.

Proposition. (a) If $\displaystyle \sum_{k = 1}^\infty a_k$ and $\displaystyle \sum_{k = 1}^\infty b_k$ converge, then $\displaystyle \sum_{k = 1}^\infty (a_k + b_k)$ converges, and

$$\sum_{k = 1}^\infty (a_k + b_k) = \sum_{k = 1}^\infty a_k + \sum_{k = 1}^\infty b_k.$$

(b) If $\displaystyle \sum_{k = 1}^\infty a_k$ converges and c is a constant, then $\displaystyle \sum_{k = 1}^\infty c \cdot a_k$ converges, and

$$\sum_{k = 1}^\infty c\cdot a_k = c\cdot \sum_{k = 1}^\infty a_k.$$

(c) If $\displaystyle \sum_{k=m}^\infty a_k$ converges and $n \ge m$ , then $\displaystyle \sum_{k=n}^\infty a_k$ converges. Likewise, if $\displaystyle \sum_{k=m}^\infty a_k$ diverges and $n \ge m$ , then $\displaystyle \sum_{k=n}^\infty a_k$ diverges.

(d) If $\displaystyle \sum_{k = 1}^\infty a_k$ converges and $\displaystyle \sum_{k = 1}^\infty b_k$ diverges, then $\displaystyle \sum_{k = 1}^\infty (a_k + b_k)$ diverges.

Proof. I'll sketch a proof of (a). I know $\displaystyle \sum_{k = 1}^\infty a_k$ and $\displaystyle \sum_{k = 1}^\infty b_k$ converge. Let $s_n$ denote the $n^{\rm th}$ partial sum of $\displaystyle \sum_{k = 1}^\infty a_k$ and let $t_n$ denote the $n^{\rm th}$ partial sum of $\displaystyle \sum_{k = 1}^\infty b_k$ . Then if $\displaystyle \sum_{k = 1}^\infty a_k = A$ and $\displaystyle \sum_{k = 1}^\infty b_k = B$ , then

$$\lim_{n \to \infty} s_n = A \quad\hbox{and}\quad \lim_{t \to \infty} b_n = B.$$

Now

$$s_n + t_n = (a_1 + a_2 + \cdots + a_n) + (b_1 + b_2 + \cdots b_n) = (a_1 + b_1) + (a_2 + b_2) + \cdots (a_n + b_n).$$

Consider

$$u_n = (a_1 + b_1) + (a_2 + b_2) + \cdots (a_n + b_n).$$

This is the $n^{\rm th}$ partial sum of $\displaystyle \sum_{k = 1}^\infty (a_k + b_k)$ . But my results on limits of sequences show that

$$\lim_{n \to \infty} s_n + \lim_{n \to \infty} t_n = \lim_{n \to \infty} (s_n + t_n) = \lim_{n \to \infty} u_n.$$

In other words,

$$\sum_{k = 1}^\infty (a_k + b_k) = \lim_{n \to \infty} u_n = A + B = \sum_{k = 1}^\infty a_k + \sum_{k = 1}^\infty b_k.\quad\halmos$$

Remark. If $\displaystyle \sum_{k = 1}^\infty a_k$ and $\displaystyle \sum_{k = 1}^\infty b_k$ both diverge, it can happen that $\displaystyle \sum_{k = 1}^\infty (a_k + b_k)$ converges. For example,

$$\sum_{n = 1}^\infty \dfrac{1}{n} \quad\hbox{and}\quad \sum_{n = 1}^\infty \left(-\dfrac{1}{n}\right) \quad\hbox{diverge}.$$

But the sum series is

$$\sum_{n = 1}^\infty \left(\dfrac{1}{n} - \dfrac{1}{n}\right) = \sum_{n = 1}^\infty 0 = 0.\quad\halmos$$

Example. Compute $\displaystyle \sum_{k = 0}^\infty \dfrac{2^n + 3^n}{4^n}$ .

By the results on geometric series, I have

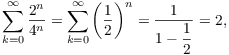
$$\sum_{k = 0}^\infty \dfrac{2^n}{4^n} = \sum_{k = 0}^\infty \left(\dfrac{1}{2}\right)^n = \dfrac{1}{1 - \dfrac{1}{2}} = 2,$$

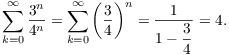
$$\sum_{k = 0}^\infty \dfrac{3^n}{4^n} = \sum_{k = 0}^\infty \left(\dfrac{3}{4}\right)^n = \dfrac{1}{1 - \dfrac{3}{4}} = 4.$$

Therefore,

$$\sum_{k = 0}^\infty \dfrac{2^n + 3^n}{4^n} = \sum_{k = 0}^\infty \dfrac{2^n}{4^n} + \sum_{k = 0}^\infty \dfrac{3^n}{4^n} = 2 + 4 = 6.\quad\halmos$$

Example. Compute

$$\dfrac{7}{3} + \dfrac{7}{3^2} + \dfrac{7}{3^3} + \cdots + \dfrac{7}{3^n} + \cdots.$$

In summation form, this is $\displaystyle \sum_{k = 1}^\infty \dfrac{7}{3^k}$ . I have

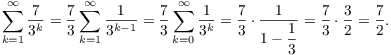
$$\sum_{k = 1}^\infty \dfrac{7}{3^k} = \dfrac{7}{3} \sum_{k = 1}^\infty \dfrac{1}{3^{k-1}} = \dfrac{7}{3} \sum_{k = 0}^\infty \dfrac{1}{3^k} = \dfrac{7}{3}\cdot \dfrac{1}{1 - \dfrac{1}{3}} = \dfrac{7}{3}\cdot \dfrac{3}{2} = \dfrac{7}{2}.$$

In the second equality, I just renumbered the terms. I can do this because both $\displaystyle \sum_{k = 1}^\infty \dfrac{1}{3^{k-1}}$ and $\displaystyle \sum_{k = 0}^\infty \dfrac{1}{3^k}$ represent the same series, namely

$$1 + \dfrac{1}{3} + \dfrac{1}{3^2} + \dfrac{1}{3^3} + \cdots.\quad\halmos$$

Sometimes it's possible to use algebraic tricks to find the sum of a convergent series. The trick in the next example uses partial fractions; it's called telescoping because of the way the terms end up cancelling in pairs.

Example. (Telescoping series) Find $\displaystyle \sum_{k = 0}^\infty \dfrac{2}{k^2 + 6 k + 8}$ .

By partial fractions,

$$\dfrac{2}{k^2 + 6 k + 8} = \dfrac{1}{k + 2} - \dfrac{1}{k + 4}.$$

Then

$$\sum_{k = 0}^\infty \left(\dfrac{1}{k + 2} - \dfrac{1}{k + 4}\right) = \left(\dfrac{1}{2} - \dfrac{1}{4}\right) + \left(\dfrac{1}{3} - \dfrac{1}{5}\right) + \left(\dfrac{1}{4} - \dfrac{1}{6}\right) + \left(\dfrac{1}{5} - \dfrac{1}{7}\right) + \left(\dfrac{1}{6} - \dfrac{1}{8}\right) + \cdots .$$

All of the fractions except for $\dfrac{1}{2}$ and $\dfrac{1}{3}$ cancel. Hence,

$$\sum_{k = 0}^\infty \dfrac{2}{k^2 + 6 k + 8} = \dfrac{1}{2} + \dfrac{1}{3} = \dfrac{5}{6}.\quad\halmos$$

In many cases, it can be very difficult to find the sum of a series. Still, it's useful to be able to tell whether a series converges or diverges. If the series converges, you can use a computer (say) to approximate the sum as closely as you want.

For this reason, this discussion of infinite series will continue by looking at tests for convergence or divergence. The first test, the Zero Limit Test, can be used to tell whether a series diverges.

Theorem. ( Zero Limit Test) If the series $\displaystyle \sum_{k = 1}^\infty a_k$ converges, the terms of the series must go to 0.

Proof. Suppose that $\displaystyle \sum_{k = 1}^\infty a_k$ converges to a sum S. I want to show that

$$\lim_{k \to \infty} a_k = 0.$$

The definition of the limit says that I have to show that I can make the $a_k$ 's lie within any tolerance $\epsilon$ of 0 by making the k's big enough. (Remember that $\epsilon$ is the Greek letter epsilon; by mathematical tradition, it's used in situations like this. But you could use another symbol if you wanted.) That is, if someone challenges me with $\epsilon$ , I have to show that I can find a large enough k so that

$$\epsilon > |a_k - 0| = |a_k|.$$

Since $\displaystyle \sum_{k = 1}^\infty a_k$ converges to a sum S, the partial sums $s_n$ must converge to S. Hence, I can choose k to be big enough so that $s_k$ and $s_{k-1}$ are within $\dfrac{1}{2} \cdot \epsilon$ of S. Then

$$|s_k - S| + |S - s_{k-1}| < \dfrac{1}{2} \cdot \epsilon + \dfrac{1}{2} \cdot \epsilon = \epsilon.$$

But by the Triangle Inequality,

$$|s_k - S| + |S - s_{k-1}| \ge |s_k - S + S - s_{k-1}| = |s_k - s_{k-1}| = |a_k|.$$

Therefore,

$$\epsilon > |s_k - S| + |S - s_{k-1}| \ge |a_k|.$$

As I noted earlier, this means that $\displaystyle \lim_{k \to \infty} a_k = 0$ .

You will more often use the following statement, which is logically equivalent to the statement I proved. I'll also call it the Zero Limit Test.

Corollary. ( Zero Limit Test) If $\displaystyle \lim_{k \to \infty} a_k \ne 0$ , then $\displaystyle \sum_{k = 1}^\infty a_k$ diverges.

Example. Apply the Zero Limit Test to $\displaystyle \sum_{k = 1}^\infty \dfrac{5 k}{7 k + 3}$ .

$$\lim_{k \to \infty} \dfrac{5 k}{7 k + 3} = \dfrac{5}{7} \ne 0.$$

Hence, the series diverges, by the Zero Limit Test.

Example. Apply the Zero Limit Test to $\displaystyle \sum_{k = 1}^\infty \cos k$ .

$$\lim_{k \to \infty} \cos k \quad\hbox{does not exist}.$$

Hence, the series diverges, by the Zero Limit Test.

Remark. A standard mistake is to use the Zero Limit Test backward. It is not true that if $\displaystyle \lim_{n \to \infty} a_n = 0$ , then the series $\displaystyle \sum_{n = 1}^\infty a_n$ converges. Counterexample: The harmonic series $\displaystyle \sum_{n = 1}^\infty \dfrac{1}{n}$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga