Taylor Series

The Taylor series for $f(x)$ at $x = c$ is

$$f(c) + f'(c)(x - c) + \dfrac{f''(c)}{2!}(x - c)^2 + \dfrac{f'''(c)}{3!}(x - c)^3 + \cdots = \sum_{n = 0}^\infty \dfrac{f^{(n)}(c)}{n!}(x - c)^n.$$

(By convention, $f^{(0)} = f$ .) When $c = 0$ , the series is called a Maclaurin series.

You can construct the series on the right provided that f is infinitely differentiable on an interval containing c. You already know how to determine the interval of convergence of the series. However, the fact that the series converges at x does not imply that the series converges to $f(x)$ .

As an example, consider the function

$$f(x) = \cases{ e^{-1/x^2} & if $x \ne 0$ \cr 0 & if $x = 0$ \cr}.$$

It is infinitely differentiable everywhere. In particular, all the derivatives of f at 0 vanish, and the Maclaurin series for f is identically 0.

Hence, the Maclaurin series for f converges for all x, but only converges to $f(x)$ at $x = 0$ .

The following result ([1], page 418) gives a sufficient condition for the Taylor series of a function to converge to the function:

Theorem. Let $f(x)$ be infinitely differentiable on $a \le x \le b$ , and let $a \le c \le b$ . Suppose there is a constant M such that $|f^{(n)}(x)| \le M$ for all $n \ge 1$ , and for all x in $N \cap [a,b]$ , where N is a neighborhood of c. Then for all $x \in N \cap [a,b]$ ,

$$f(x) = \sum_{n = 0}^\infty \dfrac{f^{(n)}(c)}{n!}(x - c)^n.$$

In other words, under reasonable conditions:

1. You can construct a Taylor series by computing the derivatives of f.

2. The series will converge to f on an interval around the expansion point. (You can find the interval of convergence as usual.)

It's tedious to have to compute lots of derivatives, and in many cases you can derive a series from another known series. Here are the series expansions for several important functions:

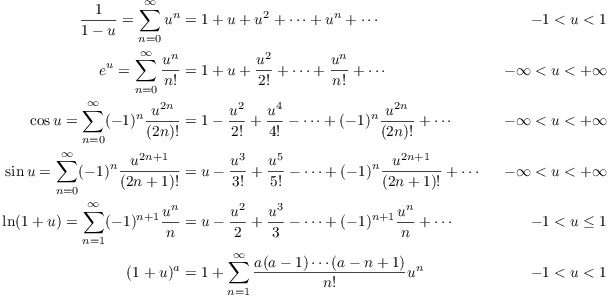
$$\eqalignno{ \dfrac{1}{1 - u} = \sum_{n = 0}^\infty u^n &= 1 + u + u^2 + \cdots + u^n + \cdots \hbox{\quad} & -1 < u < 1 \cr e^u = \sum_{n = 0}^\infty \dfrac{u^n}{n!} &= 1 + u + \dfrac{u^2}{2!} + \cdots + \dfrac{u^n}{n!} + \cdots \hbox{\quad} & -\infty < u < +\infty \cr \cos u = \sum_{n = 0}^\infty (-1)^n \dfrac{u^{2n}}{(2n)!} &= 1 - \dfrac{u^2}{2!} + \dfrac{u^4}{4!} - \cdots + (-1)^n \dfrac{u^{2n}}{(2n)!} + \cdots \hbox{\quad} & -\infty < u < +\infty \cr \sin u = \sum_{n = 0}^\infty (-1)^n \dfrac{u^{2n+1}}{(2n + 1)!} &= u - \dfrac{u^3}{3!} + \dfrac{u^5}{5!} - \cdots + (-1)^n \dfrac{u^{2n+1}}{(2n + 1)!} + \cdots \hbox{\quad} & -\infty < u < +\infty \cr \ln (1 + u) = \sum_{n=1}^\infty (-1)^{n+1} \dfrac{u^n}{n} &= u - \dfrac{u^2}{2} + \dfrac{u^3}{3} - \cdots + (-1)^{n+1} \dfrac{u^n}{n} + \cdots \hbox{\quad} & -1 < u \le 1 \cr (1 + u)^a &= 1 + \sum_{n=1}^\infty \dfrac{a(a - 1) \cdots (a - n + 1)}{n!}u^n \hbox{\quad} & -1 < u < 1 \cr } $$

Example. Find the Taylor series for $\dfrac{1}{x + 3}$ at $a = 2$ . What is its interval of convergence?

I want things to come out in powers of $x - 2$ , so I'll write the function in terms of $x - 2$ :

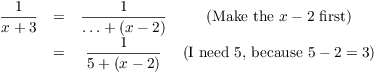
$$\matrix{ \dfrac{1}{x + 3} & = & \dfrac{1}{\ldots + (x - 2)} & (\hbox{Make the $x - 2$ first}) \cr & = & \dfrac{1}{5 + (x - 2)} & (\hbox{I need 5, because $5 - 2 = 3$}) \cr}$$

I'll use the series for $\dfrac{1}{1 - u}$ . To do this, I need $1 - u$ on the bottom. I make a "1" by factoring 5 out of the terms on the bottom, then I make a "-" by writing the "+" as "$-(-)$ ":

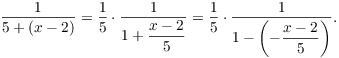
$$\dfrac{1}{5 + (x - 2)} = \dfrac{1}{5} \cdot \dfrac{1}{1 + \dfrac{x - 2}{5}} = \dfrac{1}{5} \cdot \dfrac{1}{1 - \left(-\dfrac{x - 2}{5}\right)}.$$

Let $u = -\dfrac{x - 2}{5}$ in the series for $\dfrac{1}{1 - u}$ . Then

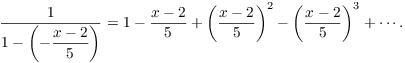
$$\dfrac{1}{1 - \left(-\dfrac{x - 2}{5}\right)} = 1 - \dfrac{x - 2}{5} + \left(\dfrac{x - 2}{5}\right)^2 - \left(\dfrac{x - 2}{5}\right)^3 + \cdots .$$

Hence,

$$\dfrac{1}{x + 3} = \dfrac{1}{5} \cdot \left[1 - \dfrac{x - 2}{5} + \left(\dfrac{x - 2}{5}\right)^2 - \left(\dfrac{x - 2}{5}\right)^3 + \cdots\right].$$

The u-series converges for $-1 < u < 1$ , so the x-series converges for $-1 < -\dfrac{x - 2}{5} < 1$ , or $-3 < x < 7$ .

Example. Find the Taylor series for $\dfrac{1}{7 - x}$ at $a = -3$ . What is its interval of convergence?

Since I'm expanding at $a = -3$ , I need powers of $x + 3$ :

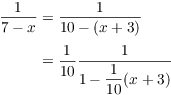
$$\eqalign{ \dfrac{1}{7 - x} & = \dfrac{1}{10 - (x + 3)} \cr \noalign{\vskip2pt} & = \dfrac{1}{10} \dfrac{1}{1 - \dfrac{1}{10} (x + 3)} \cr}$$

I let $u = \dfrac{1}{10} (x + 3)$ in the series for $\dfrac{1}{1 - u}$ :

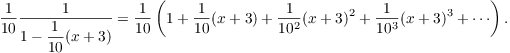
$$\dfrac{1}{10} \dfrac{1}{1 - \dfrac{1}{10} (x + 3)} = \dfrac{1}{10} \left(1 + \dfrac{1}{10} (x + 3) + \dfrac{1}{10^2} (x + 3)^2 + \dfrac{1}{10^3} (x + 3)^3 + \cdots\right).$$

In summation form, this is $\displaystyle \dfrac{1}{10} \sum_{n = 0}^\infty \dfrac{1}{10^n} (x + 3)^n$ .

Find the interval of convergence:

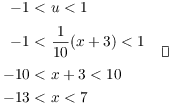
$$\eqalign{ -1 <\ & u < 1 \cr \noalign{\vskip2pt} -1 <\ & \dfrac{1}{10} (x + 3) < 1 \cr \noalign{\vskip2pt} -10 <\ & x + 3 < 10 \cr -13 <\ & x < 7 \cr} \quad\halmos$$

Example. Find the Taylor series at $c = 1$ for $e^{5 x}$ .

I need powers of $x - 1$ .

$$e^{5 x} = e^{5(x - 1) + 5} = e^{5(x - 1)} \cdot e^5 = e^5 \left(1 + 5(x - 1) + \dfrac{5^2 (x - 1)^2}{2!} + \dfrac{5^3 (x - 1)^3}{3!} + \cdots\right).$$

To get this, I let $u = 5(x - 1)$ in the series for $e^u$ .

For the interval of convergence:

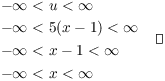
$$\eqalign{ -\infty <\ & u < \infty \cr -\infty <\ & 5(x - 1) < \infty \cr -\infty <\ & x - 1 < \infty \cr -\infty <\ & x < \infty \cr} \quad\halmos$$

Example. Find the Taylor series for $\sin x$ at $c = \dfrac{\pi}{2}$ .

I need powers of $x - \dfrac{\pi}{2}$ , so

$$\sin x = \sin \left[\left(x - \dfrac{\pi}{2}\right) + \dfrac{\pi}{2}\right].$$

Next, I'll use the angle addition formula for sine:

$$\sin (a + b) = \sin a \cos b + \sin b \cos a.$$

I set $a = x - \dfrac{\pi}{2}$ and $b = \dfrac{\pi}{2}$ . Since $\cos \dfrac{\pi}{2} = 0$ and $\sin \dfrac{\pi}{2} = 1$ , I get

$$\sin \left[\left(x - \dfrac{\pi}{2}\right) + \dfrac{\pi}{2}\right] = \cos \left(x - \dfrac{\pi}{2}\right) = 1 - \dfrac{1}{2!} \left(x - \dfrac{\pi}{2}\right)^2 + \dfrac{1}{4!} \left(x - \dfrac{\pi}{2}\right)^4 - \dfrac{1}{6!} \left(x - \dfrac{\pi}{2}\right)^6 + \cdots.\quad\halmos$$

Example. Find the Taylor series for $\ln x$ at $a = 1$ . What is its interval of convergence?

Use

$$\ln (1 + u) = \sum_{n=1}^\infty (-1)^{n+1} \dfrac{u^n}{n} = u - \dfrac{u^2}{2} + \dfrac{u^3}{3} - \cdots + (-1)^{n+1} \dfrac{u^n}{n} + \cdots.$$

I'm expanding at $a = 1$ , so I want the result to come out in powers of $x - 1$ . This is easy --- just set $u = x - 1$ :

$$\ln x = (x - 1) - \dfrac{1}{2}(x - 1)^2 + \dfrac{1}{3} (x - 1)^3 + \cdots + (-1)^{n+1} \dfrac{1}{n} (x - 1)^n + \cdots.$$

The u-series converges for $-1 < u \le 1$ , so the x-series converges for $-1 < x - 1 \le 1$ , or $0 < x \le 2$ .

Example. The quantity $\left(1 -\dfrac{v^2}{c^2}\right)^{-1/2}$ occurs in special relativity. (v is the velocity of an object, and c is the speed of light.) Approximate $\left(1 - \dfrac{v^2}{c^2}\right)^{-1/2}$ using the first two nonzero terms of the binomial series.

$$(1 + u)^a = 1 + au + \dfrac{a(a - 1)}{2!}u^2 + \cdots,$$

So for $a = -\dfrac{1}{2}$ ,

$$(1 + u)^{-1/2} = 1 - \dfrac{1}{2} u + \dfrac{3}{8} u^2 - \cdots.$$

Take $u = -\dfrac{v^2}{c^2}$ :

$$\left(1 - \dfrac{v^2}{c^2}\right)^{-1/2} = 1 + \dfrac{1}{2} \dfrac{v^2}{c^2} + \dfrac{3}{8} \dfrac{v^4}{c^4} + \cdots \approx 1 + \dfrac{1}{2}\dfrac{v^2}{c^2}.$$

The approximation is good as long as v is small compared to c.

Example. Find the Taylor series for $\dfrac{x}{2 + x}$ at $a = -1$ .

Since I'm expanding at $a = -1$ , the answer must come out in terms of powers of $x + 1$ .

Start with the function you're trying to expand. To get $x + 1$ 's in the answer, write the given function in terms of $x + 1$ :

$$\dfrac{x}{2 + x} = \dfrac{(x + 1) - 1}{1 + (x + 1)}.$$

(Notice that the work has to be legal algebra.)

I'll break up the fraction and do the pieces separately.

$$\dfrac{(x + 1) - 1}{1 + (x + 1)} = \dfrac{x + 1}{1 + (x + 1)} - \dfrac{1}{1 + (x + 1)}.$$

I want to "match" each piece against the standard series $\dfrac{1}{1 - u}$ . Here's the first piece:

$$\dfrac{x + 1}{1 + (x + 1)} = (x + 1) \dfrac{1}{1 - [-(x + 1)]}.$$

Expand $\dfrac{1}{1 - [-(x + 1)]}$ by setting $u = -(x + 1)$ in $\dfrac{1}{1 - u}$ :

$$(x + 1) \dfrac{1}{1 - [-(x + 1)]} = (x + 1)\cdot \left(1 - (x + 1) + (x + 1)^2 - (x + 1)^3 + \cdots \right) = (x + 1) - (x + 1)^2 + (x + 1)^3 - \cdots.$$

Here's the second piece:

$$\dfrac{1}{1 + (x + 1)} = \dfrac{1}{1 - [-(x + 1)]} = 1 - (x + 1) + (x + 1)^2 - (x + 1)^3 + \cdots.$$ Put the two pieces together:

$$\left[(x + 1) - (x + 1)^2 + (x + 1)^3 - \cdots\right] - \left[1 - (x + 1) + (x + 1)^2 - (x + 1)^3 + \cdots\right] =$$

$$\matrix{ & & (x + 1) & - & (x + 1)^2 & + & (x + 1)^3 & - & \cdots \cr - 1 & + & (x + 1) & - & (x + 1)^2 & + & (x + 1)^3 & - & \cdots \cr} =$$

$$-1 + 2(x + 1) - 2(x + 1)^2 + 2(x + 1)^3 - \cdots.$$

That is,

$$\dfrac{x}{2 + x} = -1 + 2(x + 1) - 2(x + 1)^2 + 2(x + 1)^3 - \cdots.\quad\halmos$$

Example. What is the Maclaurin series for $f(x) = 7x^2 - 3x + 13$ ? What is the Taylor series for $f(x) = 7x^2 - 3x + 13$ at $a = -1$ ?

The Maclaurin series for a polynomial is the polynomial: $f(x) = 7 x^2 - 3 x + 13$ .

To obtain the Taylor expansion at $a = -1$ , write the function in terms of $x + 1$ :

$$7x^2 - 3x + 13 = 7(x + 1)^2 - 17x + 6 = 7(x + 1)^2 - 17(x + 1) + 23.\quad\halmos$$

Example. Find $f^{(100)}(0)$ for $f(x) = \dfrac{1}{3 - x}$ .

The series for $\dfrac{1}{3 - x}$ at $c = 0$ is

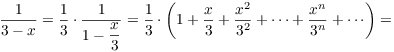
$$\dfrac{1}{3 - x} = \dfrac{1}{3}\cdot \dfrac{1}{1 - \dfrac{x}{3}} = \dfrac{1}{3} \cdot \left(1 + \dfrac{x}{3} + \dfrac{x^2}{3^2} + \cdots + \dfrac{x^n}{3^n} + \cdots\right) =$$

$$\dfrac{1}{3} + \dfrac{x}{3^2} + \dfrac{x^2}{3^3} + \cdots + \dfrac{x^n}{3^{n+1}} + \cdots.$$

The $100^{\rm th}$ degree term is $\dfrac{x^{100}}{3^{101}}$ . On the other hand, Taylor's formula says that the $100^{\rm th}$ degree term is $\dfrac{f^{(100)}(0)}{100!}x^{100}$ . Equating the coefficients, I get

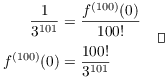
$$\eqalign{ \dfrac{1}{3^{101}} & = \dfrac{f^{(100)}(0)}{100!} \cr \noalign{\vskip2pt} f^{(100)}(0) & = \dfrac{100!}{3^{101}} \cr} \quad\halmos$$

While you can often use known series to find Taylor series, it's sometimes necessary to find a series using Taylor's formula. (In fact, that's where the "known series" come from.)

Example. Find the first four nonzero terms and the general term of the Taylor series for $f(x) = e^x$ at $a = 0$ and at $a = 1$ by computing the derivatives of f.

$$f(x) = e^x, \quad f'(x) = e^x, \quad\hbox{and in general}\quad f^{(n)}(x) = e^x.$$

For $a = 0$ , $f^{(n)}(0) = e^0 = 1$ for all n. The Taylor series at $a = 0$ is

$$f(x) = 1 + x + \dfrac{1}{2!}x^2 + \dfrac{1}{3!}x^3 + \cdots + \dfrac{1}{n!}x^n + \cdots .$$

For $a = 1$ , $f^{(n)}(1) = e^1 = e$ for all n. The Taylor series at $a = 1$ is

$$f(x) = e + e(x - 1) + \dfrac{e}{2!}(x - 1)^2 + \dfrac{3}{3!}(x - 1)^3 + \cdots + \dfrac{1}{n!}(x - 1)^n + \cdots .\quad\halmos$$

If you truncate the series expanded at c after the $n^{\rm th}$ -degree term, what's left is the $n^{\rm th}$ - degree Taylor polynomial $p_n(x; c)$ . For example, the third degree polynomial of $e^x$ at $a = 0$ is

$$p_3(x; 0) = 1 + x + \dfrac{1}{2!}x^2 + \dfrac{1}{3!}x^3.$$

Note that the "n" here refers to the largest power of x, not the number of terms. For example, the Taylor series for $\dfrac{1}{1 - x^2}$ at $a = 0$ is

$$\dfrac{1}{1 - x^2} = 1 + x^2 + x^4 + \cdots + x^{2 n} + \cdots.$$

The $2^{\rm nd}$ degree Taylor polynomial and the $3^{\rm rd}$ degree Taylor polynomial are equal:

$$p_2(x; 0) = p_3(x; 0) = 1 + x^2.\quad\halmos$$

Example. Find the $3^{\rm rd}$ degree Taylor polynomial for $f(x) = \tan x$ at $x = \dfrac{\pi}{4}$ .

$$f(x) = \tan x, \quad f'(x) = (\sec x)^2, \quad f''(x) = 2(\sec x)^2\tan x, \quad f'''(x) = 2(\sec x)^4 + 4(\sec x)^2(\tan x)^2.$$

Thus,

$$f\left(\dfrac{\pi}{4}\right) = 1, \quad f'\left(\dfrac{\pi}{4}\right) = 2, \quad f''\left(\dfrac{\pi}{4}\right) = 4, \quad f'''\left(\dfrac{\pi}{4}\right) = 16.$$

The $3^{\rm rd}$ degree Taylor polynomial is

$$p_3\left(x; \dfrac{\pi}{4}\right) = 1 + 2 \left(x - \dfrac{\pi}{4}\right) + 2 \left(x - \dfrac{\pi}{4}\right)^2 + \dfrac{8}{3} \left(x - \dfrac{\pi}{4}\right)^3.\quad\halmos$$

Example. Suppose

$$f(4) = 7, \quad f'(4) = -3, \quad f''(4) = 4, \quad f'''(4) = 12.$$

Use the $3^{\rm rd}$ degree Taylor polynomial for f at $c = 4$ to approximate $f(4.2)$ .

I have

$$p_3(x; 4) = 7 - 3(x - 4) + \dfrac{4}{2!} (x - 4)^2 + \dfrac{12}{3!} (x - 4)^3 = 7 - 3(x - 4) + 2(x - 4)^2 + 2(x - 4)^3.$$

Plug $x = 4.2$ in:

$$f(4.2) \approx 7 - 3(4.2 - 4) + 2(4.2 - 4)^2 + 2(4.2 - 4)^3 = 6.496.\quad\halmos$$

It's also possible to construct power series by integrating or differentiating other power series. A power series may be integrated or differentiated term-by-term in the interior of its interval of convergence. (You will need to check convergence at the endpoints separately.)

Example. (a) Find the Taylor series at $c = 0$ for $\dfrac{1}{8 + x}$ .

(b) Find the Taylor series at $c = 0$ for $\dfrac{1}{(8 + x)^2}$ .

(a)

$$\dfrac{1}{8 + x} = \dfrac{1}{8} \dfrac{1}{1 + \dfrac{x}{8}} = \dfrac{1}{8} \dfrac{1}{1 - \left(-\dfrac{x}{8}\right)} =$$

$$\dfrac{1}{8} \left(1 - \dfrac{x}{8} + \dfrac{x^2}{64} - \dfrac{x^3}{512} + \dfrac{x^4}{4096} - \cdots \right).\quad\halmos$$

(b) Notice that

$$\der {} x \dfrac{1}{8 + x} = -\dfrac{1}{(8 + x)^2}.$$

Hence,

$$\dfrac{1}{(8 + x)^2} = -\der {} x \dfrac{1}{8 + x} = -\der {} x \dfrac{1}{8} \left(1 - \dfrac{x}{8} + \dfrac{x^2}{64} - \dfrac{x^3}{512} + \dfrac{x^4}{4096} - \cdots \right) =$$

$$-\dfrac{1}{8} \left(-\dfrac{1}{8} + \dfrac{x}{32} - \dfrac{3 x^2}{512} + \dfrac{x^3}{1024} - \cdots\right).\quad\halmos$$

Example. (a) Find the Taylor series at $c = 0$ for $\dfrac{1}{1 + x}$ .

(b) Use the series in (a) to find the series for $\ln (1 + u)$ expanded at $c = 0$ .

(a) Put $u = -x$ in the series for $\dfrac{1}{1 - u}$ to obtain

$$\dfrac{1}{1 + x} = 1 - x + x^2 - x^3 + \cdots .$$

It converges for $-1 < x < 1$ .

(b) Integrate the series in (a) from 0 to u:

$$\ln (1 + u) = \int_0^u \left(1 - x + x^2 - x^3 + \cdots\right)\,dx = u - \dfrac{u^2}{2} + \dfrac{u^3}{3} - \dfrac{u^4}{4} + \cdots .$$

This series will converge for $-1 < u < 1$ . The left side blows up at $u = -1$ . On the other hand, if $u = 1$ ,

$$\ln 2 = 1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \cdots .$$

The right side does converges (by the Alternating Series Test), so the $\ln (1 + u)$ series converges for $-1 < u \le 1$ .

Example. Find the Taylor series for $\ln (5 - x)$ at $a = 2$ .

First, note that

$$\int_2^x \dfrac{1}{5 - t}\,dt = \left[ -\ln (5 - t) \right]_2^x = -\ln (5 - x) + \ln 3, \quad\quad\hbox{so}\quad\quad \ln (5 - x) = \ln 3 - \int_2^x \dfrac{1}{5 - t}\,dt.$$

I integrated from 2 to x because I want the expansion at $a = 2$ .

Now find the series at $a = 2$ for $\dfrac{1}{5 - t}$ :

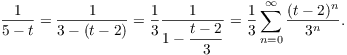
$$\dfrac{1}{5 - t} = \dfrac{1}{3 - (t - 2)} = \dfrac{1}{3} \dfrac{1}{1 - \dfrac{t - 2}{3}} = \dfrac{1}{3} \sum_{n = 0}^{\infty} \dfrac{(t - 2)^n}{3^n}.$$

Plug this series back into the integral and integrate term-by-term:

$$\ln (5 - x) = \ln 3 - \int_2^x \dfrac{1}{5 - t}\,dt = \ln 3 - \dfrac{1}{3} \int_2^x \sum_{n = 0}^{\infty} \dfrac{(t - 2)^n}{3^n}\,dt = \ln 3 - \dfrac{1}{3} \sum_{n = 0}^{\infty} \left[\dfrac{(t - 2)^{n+1}}{3^n(n + 1)}\right]_2^x =$$

$$\ln 3 - \dfrac{1}{3} \sum_{n = 0}^{\infty} \dfrac{(x - 2)^{n+1}}{3^n(n + 1)} = \ln 3 - \sum_{n = 0}^{\infty} \dfrac{(x - 2)^{n+1}}{3^{n+1}(n + 1)}.\quad\halmos$$

Example. (a) Construct the Taylor series at $c = 0$ for $\dfrac{1}{1 + t^2}$ .

(b) Use the series in (a) to construct the Taylor series at $c = 0$ for $\tan^{-1} x$ .

(c) Use the series in (b) to obtain a series for $\pi$ .

(a) I need powers of t, so

$$\dfrac{1}{1 + t^2} = \dfrac{1}{1 - (-t^2)} = 1 - t^2 + t^4 - t^6 + \cdots + (-1)^n t^{2 n} + \cdots.\quad\halmos$$

(b) Note that

$$\int_0^x \dfrac{1}{1 + t^2}\,dt = \left[\tan^{-1} t\right]_0^x = \tan^{-1} x.$$

Therefore,

$$\tan^{-1} x = \int_0^x \dfrac{1}{1 + t^2}\,dt = \int_0^x \left(1 - t^2 + t^4 - t^6 + \cdots \right)\,dt =$$

$$\left[t - \dfrac{1}{3} t^3 + \dfrac{1}{5} t^5 - \dfrac{1}{7} t^7 + \cdots \right]_0^x = x - \dfrac{1}{3} x^3 + \dfrac{1}{5} x^5 - \dfrac{1}{7} x^7 + \cdots.\quad\halmos$$

(c) Plug $x = 1$ into the series in (b), using the fact that $\tan^{-1} 1 = \dfrac{\pi}{4}$ :

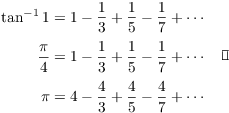
$$\eqalign{ \tan^{-1} 1 & = 1 - \dfrac{1}{3} + \dfrac{1}{5} - \dfrac{1}{7} + \cdots \cr \noalign{\vskip2pt} \dfrac{\pi}{4} & = 1 - \dfrac{1}{3} + \dfrac{1}{5} - \dfrac{1}{7} + \cdots \cr \noalign{\vskip2pt} \pi & = 4 - \dfrac{4}{3} + \dfrac{4}{5} - \dfrac{4}{7} + \cdots \cr} \quad\halmos$$

Think of a Taylor series as a "replacement" for its function. For example, you can often use a Taylor series to compute a limit or an integral by replacing a function with its series.

Example. (a) Find the first 4 nonzero terms of the Taylor series at $c = 0$ for $\ln (1 + x^3)$ .

(b) Use the series in (a) to guess the value of $\displaystyle \lim_{x \to 0} \dfrac{\ln (1 + x^3)}{x^3}$ .

(a) Let $u = x^3$ in the series for $\ln (1 + u)$ :

$$\ln(1 + x^3) = x^3 - \dfrac{1}{2} x^6 + \dfrac{1}{3} x^9 + \dfrac{1}{4} x^{12} - \cdots.\quad\halmos$$

(b) Plug the series from (a) into the limit:

$$\lim_{x \to 0} \dfrac{\ln (1 + x^3)}{x^3} = \lim_{x \to 0} \dfrac{1}{x^3} \left(x^3 - \dfrac{1}{2} x^6 + \dfrac{1}{3} x^9 + \dfrac{1}{4} x^{12} - \cdots\right) = \lim_{x \to 0} \left(1 - \dfrac{1}{2} x^3 + \dfrac{1}{3} x^6 + \dfrac{1}{4} x^9 - \cdots\right) = 1.\quad\halmos$$

Example. (a) Construct the Taylor series at $c = 0$ for $x^2 e^{-x^2}$ . (Write out at least the first 4 nonzero terms.)

(b) Use the first 3 terms of the series in (a) to approximate $\displaystyle \int_0^1 x^2 e^{-x^2}\,dx$ .

(c) Use the Alternating Series error estimate to estimate the error in (b).

(a) I set $u = -x^2$ in the series for $e^u$ :

$$e^{-x^2} = 1 - x^2 + \dfrac{x^4}{2!} - \dfrac{x^6}{3!} + \dfrac{x^8}{4!} - \cdots.$$

Multiply by $x^2$ :

$$x^2 e^{-x^2} = x^2 - x^4 + \dfrac{1}{2} x^6 - \dfrac{1}{6} x^8 + \dfrac{1}{24} x^{10} - \cdots. \quad\halmos$$

(b)

$$\int_0^1 x^2 e^{-x^2}\,dx \approx \int_0^1 \left(x^2 - x^4 + \dfrac{1}{2} x^6\right)\,dx = \left[\dfrac{1}{3} x^3 - \dfrac{1}{5} x^5 + \dfrac{1}{14} x^7\right]_0^1 = \dfrac{43}{210} = 0.20476 \ldots.\quad\halmos$$

(c) The Alternating Series error estimate says that the error is less than the next term. So I take the next term in the series in (a) and integrate:

$$\int_0^1 \dfrac{1}{6} x^8\,dx = \left[\dfrac{1}{54} x^9\right]_0^1 = \dfrac{1}{54}.$$

The error in the estimate in (b) is no greater than $\dfrac{1}{54} = 0.01851 \ldots$ .

[1] Tom M. Apostol, Mathematical Analysis. Reading, Massachusetts: Addision-Wesley Publishing Company, Inc., 1957.

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga