Trigonometric Integrals

For trig integrals involving powers of sines and cosines, there are two important cases:

1. The integral contains an odd power of sine or cosine.

2. The integral contains only even powers of sines and cosines.

I will look at the odd power case first. It turns out that the same idea can be used to integrate some powers of secants and tangents, so I'll digress to do some examples of those as well.

Example. Compute $\displaystyle \int (\sin 5 x)^3 \left(1 + 4 (\cos 5 x)^2\right)\,dx$ .

$$\int (\sin 5 x)^3 \left(1 + 4 (\cos 5 x)^2\right)\,dx = \int (\sin 5 x)^2 \left(1 + 4 (\cos 5 x)^2\right) \sin 5 x\,dx =$$

$$\int \left(1 - (\cos 5 x)^2\right) \left(1 + 4 (\cos 5 x)^2\right) \sin 5 x\,dx =$$

$$\left[u = \cos 5 x, \quad du = -5 \sin 5 x\,dx, \quad dx = -\dfrac{du}{5 \sin 5 x}\right]$$

$$-\dfrac{1}{5} \int (1 - u^2)(1 + 4 u^2)\,du = -\dfrac{1}{5} \int (1 + 3 u^2 - 4 u^4)\,du = -\dfrac{1}{5} (u + u^3 - \dfrac{4}{5} u^5) + C =$$

$$-\dfrac{1}{5}\left(\cos 5 x + (\cos 5 x)^3 - \dfrac{4}{5} (\cos 5 x)^5\right) + C = -\dfrac{1}{5} \cos 5 x - \dfrac{1}{5} (\cos 5 x)^3 + \dfrac{4}{25} (\cos 5 x)^5 + C.$$

In this example, the key point was in the second line. I obtained an integral with lots of $\cos 5 x$ 's and a single $\sin 5 x$ . This allowed me to make the substitution $u = \cos 5 x$ , because the $\sin 5 x$ was available to make $du$ .

I got the $\sin 5 x$ by "pulling it off" the odd power of $\sin 5 x$ . Then I converted the rest of the stuff to $\cos 5 x$ 's using the identity $(\sin \theta)^2 + (\cos \theta)^2 = 1$ . This is the generic procedure when you have at least one odd power of sine or cosine.

Example. Compute $\displaystyle \int \left(5 (\sin x)^{2/3} + 1\right)(\cos x)^3\,dx$ .

$$\int \left(5 (\sin x)^{2/3} + 1\right)(\cos x)^3\,dx = \int \left(5 (\sin x)^{2/3} + 1\right) \left(1 - (\sin x)^2\right)(\cos x)\,dx =$$

$$\left[u = \sin x, \quad du = \cos x\,dx, \quad dx = \dfrac{du}{\cos x}\right]$$

$$\int \left(5 u^{2/3} + 1\right)\left(1 - u^2\right)\,du = \int \left(5 u^{2/3} + 1 - 5 u^{8/3} - u^2\right)\,du = 3 u^{5/3} + u - \dfrac{15}{11}u^{11/3} - \dfrac{1}{3}u^3 + C =$$

$$3(\sin x)^{5/3} + \sin x - \dfrac{15}{11}(\sin x)^{11/3} - \dfrac{1}{3}(\sin x)^3 + C.\quad\halmos$$

If you have an integral involving sines and cosines in which all the powers are even, the method I just described usually won't work. Instead, it is better to apply the following double angle formulas:

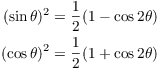
$$\eqalign{ (\sin \theta)^2 & = \dfrac{1}{2} (1 - \cos 2 \theta) \cr (\cos \theta)^2 & = \dfrac{1}{2} (1 + \cos 2 \theta) \cr}$$

Any even power of $\sin x$ or $\cos x$ can be expressed as a power of $(\sin x)^2$ or $(\cos x)^2$ . Use the identities above to substitute for $(\sin x)^2$ or $(\cos x)^2$ , and multiply out the result. The net effect is to reduce the powers that occur in the integral, while at the same time increasing the arguments ($x \to 2 x$ ).

Example. Compute $\displaystyle \int (\cos 5 x)^2 (\sin 5 x)^2\,dx$ .

$$\int (\cos 5 x)^2 (\sin 5 x)^2\,dx = \int \left(\dfrac{1}{2} (1 + \cos 10 x)\right) \left(\dfrac{1}{2} (1 - \cos 10 x)\right)\,dx = \dfrac{1}{4} \int \left(1 - (\cos 10 x)^2\right)\,dx =$$

$$\dfrac{1}{4} \int (\sin 10 x)^2\,dx = \dfrac{1}{4} \int \dfrac{1}{2} (1 - \cos 20 x)\,dx = \dfrac{1}{8} (x - \dfrac{1}{20} \sin 20 x) + C.\quad\halmos$$

Example. Compute $\displaystyle \int (\sin 5 x)^4\,dx$ .

I'll use the double angle formula (twice):

$$\int (\sin 5 x)^4\,dx = \int [(\sin 5 x)^2]^2\,dx = \int \left[\dfrac{1}{2} (1 - \cos 10 x)\right]^2\,dx = \dfrac{1}{4} \int \left[1 - 2 \cos 10 x + (\cos 10 x)^2\right]\,dx =$$

$$\dfrac{1}{4} \int \left[1 - 2 \cos 10 x + \dfrac{1}{2} (1 + \cos 20 x)\right]\,dx = \dfrac{1}{4} \left[x - \dfrac{1}{5} \sin 10 x + \dfrac{1}{2} (x + \dfrac{1}{20} \sin 20 x)\right] + c =$$

$$\dfrac{3}{8} x - \dfrac{1}{20} \sin 10 x + \dfrac{1}{160} \sin 20 x + c.\quad\halmos$$

Example. Why would it be a bad idea to use the double angle formulas to compute $\displaystyle \int (\cos x)^3\,dx$ ?

Suppose I try to apply the double angle formula for cosine:

$$\int (\cos x)^3\,dx = \int (\cos x)^2 \cos x\,dx = \int \dfrac{1}{2} (1 + \cos 2 x) \cos x\,dx.$$

The integral can be done in this form, but you either need to apply one of the angle addition formulas to $\cos 2 x \cos x$ or use integration by parts. The problem is that having trig functions with different arguments in the same integral makes the integral a bit harder to do.

It would have been better to do the integral by using the "odd power" technique:

$$\int (\cos x)^3\,dx = \int (\cos x)^2 \cos x\,dx = \int \left(1 - (\sin x)^2\right) \cos x\,dx =$$

$$\left[u = \sin x, \quad du = \cos x\,dx, \quad dx = \dfrac{du}{\cos x}\right]$$

$$\int (1 - u^2)\,du = u - \dfrac{1}{3} u^3 + C = \sin x - \dfrac{1}{3} (\sin x)^3 + C.\quad\halmos$$

In some cases, you can use trig identities to do integrals involving sine and cosine. For example, the angle addition and subtraction formulas for cosine are

$$\eqalign{ \cos (a + b) & = \cos a \cos b - \sin a \sin b \cr \cos (a - b) & = \cos a \cos b + \sin a \sin b \cr}$$

Add the two equations --- the $\sin a \sin b$ terms cancel --- and divide by 2:

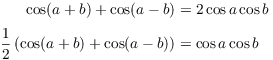
$$\eqalign{ \cos (a + b) + \cos (a - b) & = 2 \cos a \cos b \cr \noalign{\vskip2pt} \dfrac{1}{2} \left(\cos (a + b) + \cos (a - b)\right) & = \cos a \cos b \cr}$$

The formula is

$$\cos a \cos b = \dfrac{1}{2} \left(\cos (a + b) + \cos (a - b)\right).$$

If instead you subtract the $\cos (a + b)$ equation from the $\cos (a - b)$ equation and divide by 2, you obtain

$$\sin a \sin b = \dfrac{1}{2} \left(\cos (a - b) - \cos (a + b)\right).$$

Likewise, the angle addition and subtraction formulas for sine are

$$\eqalign{ \sin (a + b) & = \sin a \cos b + \sin b \cos a \cr \sin (a - b) & = \sin a \cos b - \sin b \cos a \cr}$$

Adding the equations and dividing by 2 gives

$$\sin a \cos b = \dfrac{1}{2} \left(\sin (a + b) + \sin (a - b)\right).$$

To summarize:

(a) $\cos a \cos b = \dfrac{1}{2} \left(\cos (a + b) + \cos (a - b)\right)$ .

(b) $\sin a \sin b = \dfrac{1}{2} \left(\cos (a - b) - \cos (a + b)\right)$ .

(c) $\sin a \cos b = \dfrac{1}{2} \left(\sin (a + b) + \sin (a - b)\right)$ .

You can use these identities to integrate products of sines and cosines with different arguments. (Note that you can also do these integrals using integration by parts.)

Example. Compute $\displaystyle \int \sin 8 x \cos 3 x\,dx$ .

Using the formula for $\sin a \cos b$ with $a = 8 x$ and $b = 3 x$ , I get

$$\int \sin 8 x \cos 3 x\,dx = \dfrac{1}{2} \int \left(\sin 11 x + \sin 5 x\right)\,dx = \dfrac{1}{2} \left(-\dfrac{1}{11} \cos 11 x - \dfrac{1}{5} \cos 5 x\right) + c.\quad\halmos$$

Note: If you wind up with a "negative angle" in applying the identities, you can get rid of it using the identities

$$\sin (-\theta) = -\sin \theta \quad\hbox{and}\quad \cos(-\theta) = \cos \theta).$$

To integrate some powers of secants and tangents, here are two useful approaches:

1. Use $(\sec \theta)^2 = 1 + (\tan \theta)^2$ to convert the integrand to something with lots of $\tan \theta$ 's and a single $(\sec \theta)^2$ . Then substitute $u = \tan \theta$ .

2. Use $(\tan \theta)^2 = (\sec \theta)^2 - 1$ to convert the integrand to something with lots of $\sec \theta$ 's and a single $\sec \theta \tan \theta$ . Then substitute $u = \sec \theta$ .

Example. Compute $\displaystyle \int (\sec 3 x)^4\,dx = \int (\sec 3 x)^2 (\sec 3 x)^2\,dx$ .

$$\int (\sec 3 x)^4\,dx = \int (\sec 3 x)^2 (\sec 3 x)^2\,dx = \int \left(1 + (\tan 3 x)^2\right) (\sec 3 x)^2\,dx =$$

$$\left[u = \tan 3 x, \quad du = 3 (\sec 3 x)^2\,dx, \quad dx = \dfrac{du}{3 (\sec 3 x)^2}\right]$$

$$\dfrac{1}{3} \int (1 + u^2)\,du = \dfrac{1}{3} (u + \dfrac{1}{3} u^3) + C = \dfrac{1}{3} \tan 3 x + \dfrac{1}{9} (\tan 3 x)^3 + C.$$

In this example, I pulled off a $(\sec 3 x)^2$ , then converted the rest of the stuff to $\tan 3 x$ 's using $(\sec \theta)^2 = 1 + (\tan \theta)^2$ . The $(\sec 3 x)^2$ was exactly what I needed to make $du$ for the substitution $u = \tan 3 x$ .

Notice that the argument $3 x$ did not play an important role in the problem.

Example. Compute $\displaystyle \int (\sec 6 x)(\tan 6 x)^3\,dx$ .

$$\int (\sec 6 x)(\tan 6 x)^3\,dx = \int (\tan 6 x)^2 (\sec 6 x \tan 6 x\,dx) = \int \left((\sec 6 x)^2 - 1\right)(\sec 6 x \tan 6 x\,dx) =$$

$$\left[u = \sec 6 x, \quad du = 6\sec 6 x \tan 6 x\,dx, \quad dx = \dfrac{du}{6\sec 6 x \tan 6 x}\right]$$

$$\int (u^2 - 1)(\sec 6 x \tan 6 x)\cdot \dfrac{du}{6\sec 6 x \tan 6 x} = 6 \int (u^2 - 1)\,du = 6\left(\dfrac{1}{3}u^3 - u\right) + C = 2(\sec 6 x)^3 - 6 \sec 6 x + C.$$

In this example, I pulled off a $\sec 6 x\tan 6 x$ , then converted the rest of the stuff to $\sec 6 x$ 's using $(\tan \theta)^2 = (\sec \theta)^2 - 1$ . The $\sec 6 x \tan 6 x$ was exactly what I nneded to make $du$ for the substitution $u = \sec 6 x$ .

Example. Compute $\displaystyle \int (\tan \theta)^3\,d\theta$ .

$$\int (\tan \theta)^3\,d\theta = \int (\tan \theta)^2 \tan \theta\,d\theta = \int \left((\sec \theta)^2 - 1\right) \tan \theta\,d\theta =$$

$$\int (\sec \theta)^2 \tan \theta\,d\theta - \int \tan \theta\,d\theta = \int \sec \theta (\sec \theta \tan \theta\,d\theta) - \int \dfrac{\sin \theta}{\cos \theta}\,d\theta.$$

I can do the first integral using $u = \sec \theta$ , so $du = \sec \theta \tan \theta\,d\theta$ and $d\theta = \dfrac{du}{\sec \theta \tan \theta}$ :

$$\int \sec \theta (\sec \theta \tan \theta\,d\theta) = \int u\,du = \dfrac{1}{2} u^2 + C = \dfrac{1}{2} (\sec \theta)^2 + C.$$

I can do the second integral using $w = \cos \theta$ , so $dw = -\sin \theta\,d\theta$ and $d\theta = \dfrac{dw}{-\sin \theta}$ :

$$\int \dfrac{\sin \theta}{\cos \theta}\,d\theta = \int \dfrac{1}{w}\,dw = \ln |w| + C = \ln |\cos \theta| + C.$$

Therefore,

$$\int (\tan \theta)^3\,d\theta = \dfrac{1}{2} (\sec \theta)^2 + \ln |\cos \theta| + C.\quad\halmos$$

Example. Compute $\displaystyle \int \dfrac{1}{(\sec x)^2 \tan x}\,dx$ .

In this problem, I'll use the identity

$$(\sec x)^2 - (\tan x)^2 = 1.$$

Applying this to the top of the fraction, I get

$$\int \dfrac{1}{(\sec x)^2 \tan x}\,dx = \int \dfrac{(\sec x)^2 - (\tan x)^2}{(\sec x)^2 \tan x}\,dx = \int \left(\dfrac{(\sec x)^2}{(\sec x)^2 \tan x} - \dfrac{(\tan x)^2}{(\sec x)^2 \tan x}\right)\,dx =$$

$$\int \left(\dfrac{1}{\tan x} - \dfrac{\tan x}{(\sec x)^2}\right)\,dx = \int \cot x\,dx - \int \dfrac{\sin x}{\cos x} \cdot (\cos x)^2\,dx = \ln |\sin x| - \int \sin x \cos x\,dx =$$

$$\ln |\sin x| - \dfrac{1}{2} (\sin x)^2 + C.$$

I used the formula

$$\int \cot x\,dx = \ln |\sin x| + C.$$

If you didn't know this, you could derive it by writing $\cot x = \dfrac{\cos x}{\sin x}$ . Then substitute $u = \sin x$ .

I used $u = \sin x$ to do $\displaystyle \int \sin x \cos x\,dx$ .

Example. Compute $\displaystyle \int \sec x\,dx$ .

This integral uses a trick:

$$\int \sec x\,dx = \int \sec x \cdot \dfrac{\sec x + \tan x}{\sec x + \tan x}\,dx = \int \dfrac{(\sec x)^2 + \sec x \tan x}{\sec x + \tan x}\,dx =$$

$$\left[u = \sec x + \tan x, \quad du = \left(\sec x \tan x + (\sec x)^2\right)\,dx, \quad dx = \dfrac{du}{\sec x \tan x + (\sec x)^2}\right]$$

$$\int \dfrac{(\sec x)^2 + \sec x \tan x}{u}\cdot \dfrac{du}{\sec x \tan x + (\sec x)^2} = \int \dfrac{du}{u} = \ln |u| + C = \ln |\sec x + \tan x| + C.\quad\halmos$$

Example. Compute $\displaystyle \int (\sec x)^3\,dx$ .

I can compute $\displaystyle \int (\sec x)^3\,dx$ using parts:

$$\int (\sec x)^3\,dx = \int (\sec x)(\sec x)^2\,dx = \sec x \tan x - \int \sec x(\tan x)^2\,dx =$$

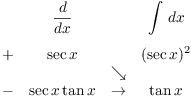
$$\matrix{& \der {} x & & \displaystyle \int\,dx \cr & & & \cr + & \sec x & & (\sec x)^2 \cr & & \searrow & \cr - & \sec x \tan x & \rightarrow & \tan x \cr}$$

$$\sec x \tan x - \int \sec x\left((\sec x)^2 - 1\right)\,dx = \sec x \tan x - \int \left((\sec x)^3 - \sec x\right)\,dx =$$

$$\sec x \tan x + \int \sec x\,dx - \int (\sec x)^3\,dx = \sec x \tan x + \ln |\sec x + \tan x| - \int (\sec x)^3\,dx.$$

Thus,

$$\eqalign{ \int (\sec x)^3\,dx & = \sec x \tan x + \ln |\sec x + \tan x| - \int (\sec x)^3\,dx \cr 2 \int (\sec x)^3\,dx & = \sec x \tan x + \ln |\sec x + \tan x| \cr \int (\sec x)^3\,dx & = \dfrac{1}{2}\sec x \tan x + \dfrac{1}{2}\ln |\sec x + \tan x| + C \cr}$$

This integral also comes up a lot, so you should make a note of it.

Remark. Using the methods of the last two examples, you can show:

$$\int \csc x\,dx = -\ln |\csc x + \cot x| + C.$$

$$\int (\csc x)^3\,dx = -\dfrac{1}{2} \csc x \cot x - \dfrac{1}{2} \ln |\csc x + \cot x| + C.$$

In general, integrals involving powers of cosecant and cotangent use the same ideas as integrals involving powers of secant and tangent.

Example. Compute $\displaystyle \int (\cot 5 x)^2\,dx$ .

Remember the trig identity

$$(\csc x)^2 = 1 + (\cot x)^2.$$

So

$$\int (\cot 5 x)^2\,dx = \int \left((\csc 5 x)^2 - 1\right)\,dx = -\dfrac{1}{5}\cot 5 x - x + C.\quad\halmos$$

The examples show that certain patterns that arise in trig integrals are good, in the sense that they allow you to do a substitution which makes the integral easy. Here is a review of some of the "good patterns":

(a) Lots of $\cos x$ 's and a single $\sin x$ .

(b) Lots of $\sin x$ 's and a single $\cos x$ .

(c) Lots of $\tan x$ 's and a single $(\sec x)^2$ .

(d) Lots of $\sec x$ 's and a single $\sec x \tan x$ .

(e) Lots of $\cot x$ 's and a single $(\csc x)^2$ .

(f) Lots of $\csc x$ 's and a single $\csc x \cot x$ .

You should aim for these patterns whenever possible.

Finally, I'll note that you can sometimes use integration by parts to obtain recursion formulas which reduce the integral of a power of a trig function to the integral of a smaller power.

Example. Derive a recursion formula for $\displaystyle \int (\sin x)^n\,dx$ for $n \ge 2$ .

Integrate $\displaystyle \int (\sin x)^n\,dx$ by parts:

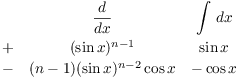
$$\matrix{ & \displaystyle \der {} x & \displaystyle \int\,dx \cr \noalign{\vskip2pt} + & (\sin x)^{n - 1} & \sin x \cr \noalign{\vskip2pt} - & (n - 1) (\sin x)^{n - 2} \cos x & -\cos x \cr}$$

$$\int (\sin x)^n\,dx = -(\sin x)^{n - 1} \cos x + (n - 1) \int (\sin x)^{n - 2} (\cos x)^2\,dx =$$

$$-(\sin x)^{n - 1} \cos x + (n - 1) \int (\sin x)^{n - 2} [1 - (\sin x)^2]\,dx =$$

$$-(\sin x)^{n - 1} \cos x + (n - 1) \int (\sin x)^{n - 2}\,dx - (n - 1) \int (\sin x)^n\,dx.$$

After integrating by parts, I used the identity $(\cos x)^2 = 1 - (\sin x)^2$ . I multiplied out the terms in the integral, then broke the integral up into two integrals.

Next, add $\displaystyle (n - 1) \int (\sin x)^n\,dx$ to both sides of the equation:

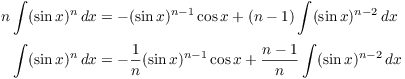
$$\eqalign{ n \int (\sin x)^n\,dx & = -(\sin x)^{n - 1} \cos x + (n - 1) \int (\sin x)^{n - 2}\,dx \cr \noalign{\vskip2pt} \int (\sin x)^n\,dx & = -\dfrac{1}{n} (\sin x)^{n - 1} \cos x + \dfrac{n - 1}{n} \int (\sin x)^{n - 2}\,dx \cr}$$

The last equation is the recursion formula. It reduces the integral of a power of sine to some stuff ($-\dfrac{1}{n} (\sin x)^{n - 1} \cos x$ ) plus the integral of a power of sine that is smaller by 2.

Here's how the formula would apply if $n = 3$ :

$$\int (\sin x)^3\,dx = -\dfrac{1}{3} (\sin x)^2 \cos x + \dfrac{2}{3} \int \sin x\,dx = -\dfrac{1}{3} (\sin x)^2 \cos x - \dfrac{2}{3} \cos x + c.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga