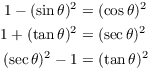
Trigonometric Substitution

Trigonometric substitution ("trig substitution") reduces certain integrals to integrals of trig functions. The idea is to match the given integral against one of the following trig identities:

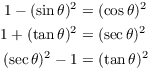
$\eqalign { 1 - (\sin \theta)^2 &= (\cos \theta)^2\cr 1 + (\tan \theta)^2 &= (\sec \theta)^2\cr (\sec \theta)^2 - 1 &= (\tan \theta)^2\cr }$

(a) If the integral contains an expression of the form , try a substitution based on the first identity: $x = a \sin \theta$ .

(b) If the integral contains an expression of the form , try a substitution based on the second identity: $x = a \tan \theta$ .

(c) If the integral contains an expression of the form , try a substitution based on the third identity: $x = a \sec \theta$ .

If you don't obtain one of the identities above after substituting, you've probably used the wrong substitution.

Example. Compute $\displaystyle \int \dfrac{1}{(1 - x^2)^{5/2}}\,dx$ .

The expression " " leads me to try

$x = \sin \theta, \quad\hbox{so}\quad dx = \cos \theta\,d\theta.$

Plug in:

$\int \dfrac{1}{(1 - x^2)^{5/2}}\,dx = \int \dfrac{1}{[1 - (\sin \theta)^2]^{5/2}} \cdot \cos \theta\,d\theta = \int \dfrac{1}{[(\cos \theta)^2]^{5/2}} \cdot \cos \theta\,d\theta = \int \dfrac{1}{(\cos \theta)^5} \cdot \cos \theta\,d\theta =$

$\int \dfrac{1}{(\cos \theta)^4}\,d\theta = \int (\sec \theta)^4\,d\theta = \int (\sec \theta)^2 (\sec \theta)^2\,d\theta = \int [1 + (\tan \theta)^2] (\sec \theta)^2\,d\theta = \int (1 + u^2)\,du =$

$\left[u = \tan \theta, \quad du = (\sec \theta)^2\,d\theta, \quad d\theta = \dfrac{du}{(\sec \theta)^2}\right]$

$u + \dfrac{1}{3} u^3 + c = \tan \theta + \dfrac{1}{3} (\tan \theta)^3 + c.$

To put the x back, I draw a right triangle. The substitution was

$\sin \theta = x = \dfrac{x}{1}.$

Since sine is the opposite side divided by the hypotenuse, I get:

$\hfil\raise0.5in\hbox{$\left[x = \sin \theta, \quad dx = \cos \theta\,d\theta\right]$} \hskip0.5in \hbox{\epsfysize=1in \epsffile{trig-substitution-1.eps}}\hfil$

I found the adjacent side $\sqrt{1 - x^2}$ using Pythagoras. From the triangle, I see that $\tan \theta = \dfrac{x}{\sqrt{1 - x^2}}$ . Plugging this back in, I get

$\tan \theta + \dfrac{1}{3} (\tan \theta)^3 + c = \dfrac{x}{\sqrt{1 - x^2}} + \dfrac{1}{3} \dfrac{x^3}{(1 - x^2)^{3/2}} + c.\quad\halmos$

Example. Compute $\displaystyle \int (4 - x^2)^{3/2}\,dx$ .

To "match" the "4" in " ", I use $x = 2 \sin \theta$ (since ). Differentiation gives $\der x \theta = 2 \cos \theta$ , so $dx = 2 \cos \theta\,d\,\theta$ . I plug in and simplify:

$\int (4 - x^2)^{3/2}\,dx = \int \left(4 - 4 (\sin \theta)^2\right)^{3/2} (2 \cos \theta)\,d\theta =$

$\left[x = 2 \sin \theta,\quad dx = 2 \cos \theta\,d\theta\right]$

$\int \left(4 (\cos \theta)^2\right)^{3/2} (2 \cos \theta)\,d\theta = 16 \int (\cos \theta)^4\,d\theta.$

I have an even power of cosine, so I need to use the double angle formula for $(\cos \theta)^2$ :

$16 \int (\cos \theta)^4\,d\theta = 16 \int \left((\cos \theta)^2\right)^2\,d\theta = 16 \int \left(\dfrac{1}{2} (1 + \cos 2 \theta)\right)^2\,d\theta = 4 \int \left(1 + 2 \cos 2 \theta + (\cos 2 \theta)^2\right)\,d\theta =$

$4 \int \left(1 + 2 \cos 2 \theta + \left(\dfrac{1}{2} (1 + \cos 4 \theta)\right)\right)\,d\theta = 4 \left(\theta + \sin 2 \theta + \dfrac{1}{2} (\theta + \dfrac{1}{4} \sin 4 \theta)\right) + C =$

$6 \theta + 4 \sin 2 \theta + \dfrac{1}{2} \sin 4 \theta + C.$

I need to put the x's back.

For the terms $4 \sin 2 \theta$ and $\dfrac{1}{2} \sin 4 \theta$ , I need to express everything in terms of trig functions of $\theta$ (as opposed to $2 \theta$ or $4 \theta$ ). I use the double angle formulas for sine:

$\eqalign{ \sin 2 \theta & = 2 \sin \theta \cos \theta \cr \sin 4 \theta & = 2 \sin 2 \theta \cos 2 \theta = 2 (2 \sin \theta \cos \theta)\left(2 (\cos \theta)^2 - 1\right) = 4 \sin \theta \cos \theta \left(2 (\cos \theta)^2 - 1\right) \cr}$

Therefore,

$\int (4 - x^2)^{3/2}\,dx = 6 \theta + 8 \sin \theta \cos \theta + 2 \sin \theta \cos \theta \left(2 (\cos \theta)^2 - 1\right) + C = 6 \theta + 6 \sin \theta \cos \theta + 4 (\cos \theta)^3 \sin \theta + C.$

The " $\theta$ " in the first term is not inside a trig function. For that term, $x = 2 \sin \theta$ gives $\sin \theta = \dfrac{x}{2}$ , so $\theta = \sin^{-1} \dfrac{x}{2}$ .

For the second and third terms, draw a right triangle which shows the substitution.

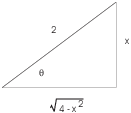
$\hbox{\epsfysize=1in \epsffile{trig-substitution-2.eps}}$

The triangle shows $\sin \theta = \dfrac{x}{2}$ --- the opposite side is x and the hypotenuse is 2 --- and by Pythagoras the third side is $\sqrt{4 - x^2}$ . Therefore,

$\sin \theta = \dfrac{x}{2} \quad\hbox{and}\quad \cos \theta = \dfrac{\sqrt{4 - x^2}}{2}.$

Plugging all of this into the last expression, I have

$\int (1 - x^2)^{3/2}\,dx = 6 \theta + 6 \sin \theta \cos \theta + 4 (\cos \theta)^3 \sin \theta + C = 6 \sin^{-1} \dfrac{x}{2} + \dfrac{3}{2} x \sqrt{4 - x^2} + \dfrac{1}{4} x (4 - x^2)^{3/2} + C.\quad\halmos$

Example. Compute $\displaystyle \int \dfrac{dx}{\sqrt{25 + x^2}}$ .

looks like $1 + (\tan \theta)^2$ , so let $x = 5 \tan \theta$ . Then $dx = 5(\sec \theta)^2\,d\theta$ , so

$\int \dfrac{dx}{\sqrt{25 + x^2}} = \int \dfrac{5(\sec \theta)^2\,d\theta} {\sqrt{25 + 25(\tan \theta)^2}} = \int \dfrac{5(\sec \theta)^2\,d\theta}{\sqrt{25(\sec \theta)^2}} = \int \dfrac{5(\sec \theta)^2\,d\theta}{5\sec \theta} = \int \sec \theta\,d\theta =$

$\hfil\raise0.5in\hbox{$\left[x = 5 \tan \theta, \quad dx = 5 (\sec \theta)^2\,d\theta\right]$} \hskip0.5in \hbox{\epsfysize=1in \epsffile{trig-substitution-3.eps}}\hfil$

$\ln |\sec \theta + \tan \theta| + C = \ln \left|\dfrac{\sqrt{25 + x^2}}{5} + \dfrac{x}{5}\right| + C.\quad\halmos$

Example. Compute $\displaystyle \int \dfrac{x\,dx}{\sqrt{25 + x^2}}$ .

This could be done using $x = 5\tan \theta$ . But it's easier to do a u-substitution:

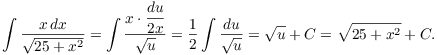
$\int \dfrac{x\,dx}{\sqrt{25 + x^2}} = \int \dfrac{x\cdot \dfrac{du}{2x}}{\sqrt{u}} = \dfrac{1}{2} \int \dfrac{du}{\sqrt{u}} = \sqrt{u} + C = \sqrt{25 + x^2} + C.$

$\left[u = 25 + x^2, \quad du = 2x\,dx, \quad dx = \dfrac{du}{2x}\right]\quad\halmos$

Example. Compute $\displaystyle \int \sqrt{x^2 - 4}\,dx$ .

looks like $(\sec \theta)^2 - 1$ , so let $x = 2\sec \theta$ . Then $dx = 2\sec \theta \tan \theta\,d\theta$ , and

$\int \sqrt{x^2 - 4}\,dx = \int \sqrt{4(\sec \theta)^2 - 4}(2\sec \theta \tan \theta\,d\theta) = \int \sqrt{4(\tan \theta)^2}(2\sec \theta \tan \theta\,d\theta) =$

$\hfil\raise0.5in\hbox{$\left[x = 2 \sec \theta, \quad dx = 2 \sec \theta \tan \theta\,d\theta\right]$} \hskip0.5in \hbox{\epsfysize=1in \epsffile{trig-substitution-4.eps}}\hfil$

$\int (2\tan \theta)(2\sec \theta \tan \theta\,d\theta) = 4 \int \sec \theta (\tan \theta)^2\,d\theta = 4 \int \sec \theta\left((\sec \theta)^2 - 1\right)\,d\theta =$

$4 \int (\sec \theta)^3\,d\theta - 4\int \sec \theta\,d\theta = 2 \sec \theta \tan \theta + 2\ln |\sec \theta + \tan \theta| - 4 \ln |\sec \theta + \tan \theta| + C =$

$2 \sec \theta \tan \theta - 2\ln |\sec \theta + \tan \theta| = \dfrac{1}{2} x \sqrt{x^2 - 4} - 2 \ln \left|\dfrac{x}{2} + \dfrac{\sqrt{x^2 - 4}}{2}\right| + C.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page