Volumes of Revolution

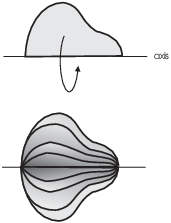
Start with an area --- a planar region --- which you can imagine as a piece of cardboard. The cardboard is attached by one edge to a stick (the axis of revolution). As you spin the stick, the area revolves and sweeps out a region in space.

$\hbox{\epsfysize=2in \epsffile{volumes-by-circular-slices-1.eps}}$

The problem is to find the volume of revolution --- the volume of the region in space which is swept out by the area.

If the region is like the one above, you can find its volume by cutting the region into circular slices perpendicular to the axis.

$\hbox{\epsfysize=2in \epsffile{volumes-by-circular-slices-2.eps}}$

(We'll have to make some adjustments if there is space between the area being revolved and the axis.)

If the radius of a slice is r, then its volume is

$\pi r^2\cdot (\hbox{thickness}).$

In the simplest case, the radius is given by a nonegative function , and the volume is generated by revolving the area under the graph of f from to around the x-axis. As usual, I divide the interval $a \le x \le b$ up into pieces, with the k-th piece having width $\Delta x_k$ . I pick an x-value in the k-th piece, say . Then the volume of the k-th circular slice will be

$\pi f(x_k)^2 \Delta x_k.$

The total volume is approximated by adding up the volumes of the slices, as you can see in the picture above. So if I have n slices, then

$(\hbox{total volume}) \approx \sum_{k=1}^n \pi f(x_k)^2 \Delta x_k.$

To get the exact volume, I shrink the slices, letting the thickness $\Delta x_k$ of a typical slice go to 0:

$(\hbox{total volume}) = \lim_{\Delta x_k \to 0} \sum_{k=1}^n \pi f(x_k)^2 \Delta x_k.$

The expression on the right is a Riemann sum for $\displaystyle \int_a^b \pi f(x)^2\,dx$ . So

$(\hbox{total volume}) = \int_a^b \pi f(x)^2\,dx.$

We get a similar expression if the area is revolved about the y-axis.

As with area problems, I'll use a shortcut rather than writing down the Riemann sum. I'll simply write

$(\hbox{total volume}) = \int_a^b \pi r^2 \cdot (\hbox{thickness}).$

In the examples I do, the axis of revolution will always be parallel to the x-axis or the y-axis. If the axis is parallel to the x-axis, the thickness is ; if the axis is parallel to the y-axis, the thickness is . These correspond to $\Delta x_k$ or $\Delta y_k$ in the Riemann sum.

The radius r is the distance from the axis of revolution to the edge of the slice. It will usually be given by a function specified in the problem which determines the region which is being revolved. You'll see how this works in the examples below.

Example. The region under $y = \sin x$ from to $x = \pi$ is revolved about the x-axis. Find the volume generated.

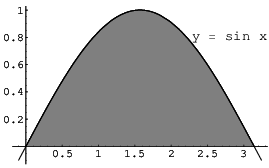
$\hbox{\epsfysize=1.5in \epsffile{volumes-by-circular-slices-3.eps}}$

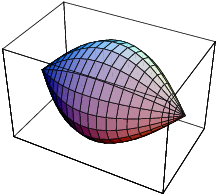
$\hbox{\epsfysize=1.75in \epsffile{volumes-by-circular-slices-4.eps}}$

To find the volume, cut the solid into circular slices perpendicular to the axis:

$\hbox{\epsfysize=1.75in \epsffile{volumes-by-circular-slices-5.eps}}$

The radius of a typical slice is the height of the curve: $r = \sin x$ . The thickness is . Thus, the volume of a typical slice is $\pi (\sin x)^2\,dx$ --- (circle area) times (thickness). So the total volume is

$V = \int_0^\pi \pi(\sin x)^2\,dx = \pi \int_0^\pi \dfrac{1}{2} (1 - \cos 2 x)\,dx = \dfrac{\pi}{2}\left[x - \dfrac{1}{2} \sin 2 x\right]_0^\pi = \dfrac{\pi^2}{2} = 4.93480 \ldots.$

I used the double angle formula for $(\sin x)^2$ to compute the antiderivative.

Example. The area bounded by and the x-axis is revolved about the x-axis. Find the volume of the solid generated.

The region is the area under the parabola from to .

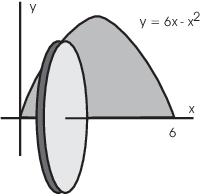
$\hbox{\epsfysize=1.75in \epsffile{volumes-by-circular-slices-6.eps}}$

In the picture above, I've superimposed a typical slice over the picture of the area being revolved. You can see that the radius of a typical slice is the height of the curve: . The thickness of a typical slice is .

Thus, the total volume is

$V = \int_0^6 \pi (6 x - x^2)^2\,dx = \pi \int_0^6 (36 x^2 - 12 x^3 + x^4)\,dx = \pi \left[12 x^3 - 3 x^4 + \dfrac{1}{5} x^5\right]_0^6 = \dfrac{1296 \pi}{5} = 814.30081 \ldots.\quad\halmos$

Example. Show that the volume of a sphere of radius a is $\dfrac{4}{3} \pi a^3$ .

$\hbox{\epsfysize=1.5in \epsffile{volumes-by-circular-slices-7.eps}}$

The equation of the circle of radius a centered at the origin is

The idea is to revolve the area under the top half of the circle around the x-axis to generate the sphere. The equation of the top half is

$y = \sqrt{a^2 - x^2}.$

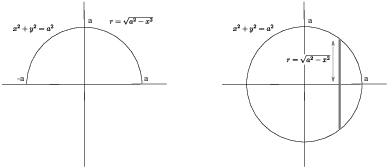
$\hbox{\epsfysize=1.5in \epsffile{volumes-by-circular-slices-8.eps}} \hskip0.5in \hbox{\epsfysize=1.5in \epsffile{volumes-by-circular-slices-9.eps}}$

I'll use circular slices. A typical slice has radius $r = \sqrt{a^2 - x^2}$ . The volume is

$\int_{-a}^a \pi (\sqrt{a^2 - x^2})^2\,dx = \pi \int_{-a}^a (a^2 - x^2)\,dx = \pi \left[a^2 x - \dfrac{1}{3} x^3\right]_{-a}^a = \dfrac{4}{3} \pi a^3.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page