Volumes by Cross Sections

Suppose a solid extends from to . Suppose that when it is cut by planes perpendicular to the x-axis, the cross-section of the solid cut by such a plane has area . As usual, I divide the interval from a to b into subintervals of width $\Delta x$ (say $\Delta x = \dfrac{b - a}{n}$ for some n).

$\hbox{\epsfysize=1.75in \epsffile{volumes-by-cross-sections-1.eps}}$

On a typical subinterval, I have cross-sections of areas and $A(x + \Delta x)$ . It's reasonable to suppose that if the function is "nice enough", there should be a number $\overline{x}$ between x and $x + \Delta x$ such that the volume of the small cross-section (or "slice") of thickness $\Delta x$ from x to $x + \Delta x$ is exactly

$A(\overline{x}) \cdot \Delta x.$

Adding up the volumes of such cross-sections gives the volume of the solid:

$V = \sum A(\overline{x}) \cdot \Delta x.$

Replacing $A(\overline{x})$ with only gives an approximation:

$V \approx \sum A(x) \cdot \Delta x.$

But if I take the limit as $\Delta x \to 0$ , then if is "nice enough" (for example, continuous as a function of x), then in the limit I will get the exact volume. It will be given by

$V = \lim_{\Delta x \to 0} \sum A(x) \cdot \Delta x = \int_a^b A(x)\,dx.$

Example. The cross-sections of a solid in planes perpendicular to the x-axis have area

Find the volume of the solid from to .

Since the cross-sectional area function is given, I just integrate from 0 to 1:

$V = \int_0^1 (6 x^2 + 5)\,dx = \left[2 x^3 + 5 x\right]_0^1 = 7.\quad\halmos$

In the problems that follow, you need to determine the cross-sectional area function. In many cases, it comes from an area formula from geometry. Here are some common ones.

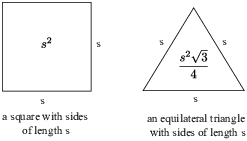
$\hbox{\epsfysize=1.25in \epsffile{volumes-by-cross-sections-2.eps}}$

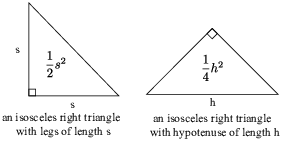
$\hbox{\epsfysize=1.25in \epsffile{volumes-by-cross-sections-3.eps}}$

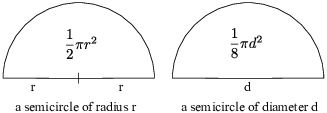
$\hbox{\epsfysize=1in \epsffile{volumes-by-cross-sections-4.eps}}$

Example. The base of a solid is the region in the x-y plane bounded above by and below by the x-axis, from to . The cross-sections in planes perpendicular to the x-axis are squares with one side lying in the x-y plane. Find the volume of the solid.

$$$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cross-sections-5.eps}} \hskip0.5 in \hbox{\epsfysize=1.5in \epsffile{volumes-by-cross-sections-6.eps}}$$ The first picture shows some of the square cross-sections. The second picture shows the base of the solid, with the edge of one of the square cross-sections drawn. The edge of the square is $x^2$, so the area of the cross-section is $(x^2)^2$. The volume is$

$V = \int_0^1 (x^2)^2\,dx = \int_0^1 x^4\,dx = \left[\dfrac{1}{5}x^5\right]_0^1 = \dfrac{1}{5}.\quad\halmos$

Example. The base of a solid is the region in the x-y plane bounded above by and below by the x-axis. The cross-sections in planes perpendicular to the x-axis are equilateral triangles with one side lying in the x-y plane. Find the volume of the solid.

The base is bounded by and the x-axis. The parabola intersects the x-axis at and .

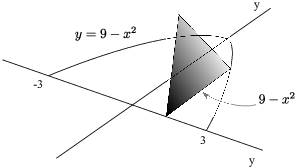
$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cross-sections-7.eps}}$

The picture shows a typical cross-section. It's an equilateral triangle, and its side has length . Hence, the area of the cross-section is $\dfrac{\sqrt{3}}{4}(9 - x^2)^2$ .

The volume is

$V = \int_{-3}^3 \dfrac{\sqrt{3}}{4} (9 - x^2)^2\,dx = \dfrac{\sqrt{3}}{4} \int_{-3}^3 (81 - 18 x^2 + x^4)\,dx = \dfrac{\sqrt{3}}{4} \left[81 x - 6 x^3 + \dfrac{1}{5}x^5\right]_{-3}^3 =$

$\dfrac{324 \sqrt{3}}{5} = 112.23689 \ldots.\quad\halmos$

Example. The base of a solid is the region in the first quadrant cut off by the line . The cross-sections in planes perpendicular to the x-axis are semicircles with their diameters lying in the x-y plane. Find the volume of the solid.

$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cross-sections-8.eps}}$

The diameter of a typical cross-section is , so the radius is $\dfrac{8 - x}{2}$ . The volume is

$V = \int_0^8 \dfrac{\pi}{2}\left(\dfrac{8 - x}{2}\right)^2\,dx = \dfrac{\pi}{8} \int_0^8 (8 - x)^2\,dx = \dfrac{\pi}{8} \left[-\dfrac{1}{3}(8 - x)^3\right]_0^8 = \dfrac{64 \pi}{3} = 67.02064 \ldots.\quad\halmos$

Example. The base of a solid is the region in the first quadrant cut off by the line . The cross-sections in planes perpendicular to the x-axis are isosceles right triangles with the hypotenuses lying in the x-y plane. Find the volume of the solid.

$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cross-sections-9.eps}}$

Since the hypotenuse of a typical triangle is , the side of such a triangle is $\dfrac{1 - x}{\sqrt{2}}$ . The area of a triangular slice is one-half the base times the height, which is

$\dfrac{1}{2} \left(\dfrac{1 - x}{\sqrt{2}}\right) \left(\dfrac{1 - x}{\sqrt{2}}\right) = \dfrac{1}{4} (1 - x)^2.$

The volume is

$V = \dfrac{1}{4} \int_0^1 (1 - x)^2\,dx = \dfrac{1}{4} \left[-\dfrac{1}{3}(1 - x)^3\right]_0^1 = \dfrac{1}{12}.\quad\halmos$

Example. A solid hemisphere of radius 4 has its base in the x-y-plane. It is cut by a plane parallel to the x-y-plane and 1 unit above it. Find the volume of the part of the hemisphere which lies between the cutting plane and the x-y-plane.

In this problem, you have to decide how to slice the solid in order to give cross-sections whose areas you can compute. Slicing the solid by planes parallel to the x-y plane produces circular disks.

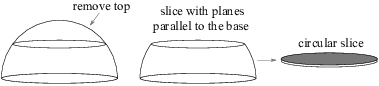
$\hbox{\epsfysize=0.75in \epsffile{volumes-by-cross-sections-10.eps}}$

The next picture shows the solid in cross-section, with a typical slice drawn.

$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cross-sections-11.eps}}$

By Pythagoras' theorem, the radius of a disk lying z units above the x-y-plane is $\sqrt{16 - z^2}$ , so its cross-sectional area is $\pi (16 - z^2)$ .

The volume is

$\int_0^1 \pi (16 - z^2)\,dz = \pi \left[16 z - \dfrac{1}{3} z^3\right]_0^1 = \dfrac{47 \pi}{3} = 49.21828 \ldots.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page