Volumes by Cylindrical Shells

In this section, we'll consider another method for computing the volume of a solid of revolution. The idea is to break up the solid into cylindrical shells. The solid will be built up of an "infinite number" of cylinders, nested inside one another.

$$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cylindrical-shells-1.eps}}$$

Suppose the region being revolved is bounded by a top curve and a bottom curve, over some interval on the x-axis. Consider a small piece of the region between the top and bottom curves and extending horizontally from r to $r + \Delta x$ :

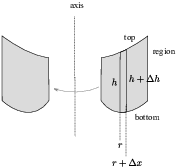
$$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cylindrical-shells-2.eps}}$$

r is the distance from the axis of revolution to the edge of the small piece. It might not be the same as x if the axis of revolution is not the x-axis.

The height of the small piece varies from h to $h + \Delta h$ . Note that $\Delta h$ could be positive, negative, or 0. For any x-coordinate, this height is just the top curve minus the bottom curve.

As the small piece revolves about the axis of revolution, it sweeps out a solid which is approximately the region between two cylinders:

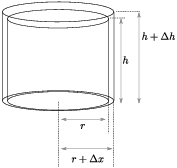
$$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cylindrical-shells-3.eps}}$$

We can approximate the volume of this region as follows. The cross-sectional area perpendicular to the axis of revolution is the area between two circles of radii r and $r + \Delta x$ :

$$\pi [(r + \Delta x)^2 - r^2] = 2 \pi r \Delta x + \pi (\Delta x)^2.$$

For the height, I'll use $\overline{h}$ , the average value of h over the interval.

The volume of the solid swept out by the small piece is

$$(2 \pi r \Delta x + \pi (\Delta x)^2) \cdot \overline{h}.$$

If I sum the volumes of these solids and let the length of the interval $\Delta x$ go to 0, I should get the volume of the solid of revolution.

As $\Delta x \to 0$ , I can neglect the term $\pi (\Delta x)^2$ , since it is small compared to the other term $2 \pi r \Delta x$ . In addition, $\overline{h} \to h$ , where h is just the difference between the top and bottom curves. So I have a sum of the form

$$\sum 2 \pi r h \Delta x.$$

In the limit as $\Delta x \to 0$ , this gives a Riemann sum for the integral

$$\int_a^b 2 \pi r h\,dx.$$

If the axis of revolution is horizontal (parallel to the x-axis), the formula is

$$\int_a^b 2 \pi r h\,dy.$$

Example. The area under $y = x^2 + 1$ from $x = 0$ to $x = 1$ is revolved about the y-axis. Find the volume generated.

To do these problems I'll draw a cross-sectional picture. It shows the original region, and a copy of the region revolved to the other side of the axis. I'll draw a typical shell, showing the two places where the shell "goes through" the x-y-plane as vertical rectangles.

$$\hbox{\epsfysize=1.75in \epsffile{volumes-by-cylindrical-shells-4.eps}} \hskip0.5in \hbox{\epsfysize=1.75in \epsffile{volumes-by-cylindrical-shells-5.eps}}$$

The first picture shows the cross-sectional picture. The second picture shows the cylinder drawn in the cross-section.

In the future, I'll just draw the cross-sectional picture.

The height of a typical cylindrical shell is $h = x^2 + 1$ . The radius of a typical cylindrical shell is $r = x$ . The volume of the solid is

$$V = \int_0^1 2 \pi x(x^2 + 1)\,dx = 2 \pi \int_0^1 (x^3 + x)\,dx = 2 \pi \left[\dfrac{1}{4}x^4 + \dfrac{1}{2}x^2\right]_0^1 = \dfrac{3 \pi}{2} \approx 4.71239.\quad\halmos$$

Example. The region bounded by $y = x^2$ and $y = 1$ is revolved about the x-axis. Find the volume of the solid generated.

In this case, the shells go "sideways", parallel to the x-axis:

$$\hbox{\epsfysize=1.75in \epsffile{volumes-by-cylindrical-shells-6.eps}}$$

The height of a typical cylindrical shell is

$$h = (\hbox{right}) - (\hbox{left}) = \sqrt{y} - (-\sqrt{y}) = 2 \sqrt{y}.$$

The radius of a typical cylindrical shell is $r = y$ , the distance from the axis (the x-axis) to the side of the shell. The volume of the solid is

$$V = \int_0^1 2 \pi y \cdot 2 \sqrt{y}\,dy = 4 \pi \int_0^1 y^{3/2}\,dy = 4 \pi\left[\dfrac{2}{5} y^{5/2}\right]_0^1 = \dfrac{8 \pi}{5} = 5.02654 \ldots.\quad\halmos$$

Example. The area under $y = x$ from $x = 0$ to $x = 1$ is revolved about the y-axis. Find the volume of the solid generated using: (a) Circular washers, and (b) Cylindrical shells.

(a) Using washers, the inner radius of a typical washer is y and the outer radius of a typical washer is 1.

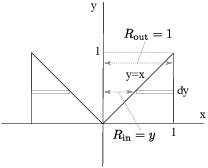
$$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cylindrical-shells-7.eps}}$$

The volume of the solid is

$$V = \int_0^1 \pi (1^2 - y^2)\,dy = \pi \left[y - \dfrac{1}{3} y^3\right]_0^1 = \dfrac{2 \pi}{3} = 2.09439 \ldots.$$

(b) Using cylindrical shells, the height of a typical cylindrical shell is $h = x$ and the radius of a typical cylindrical shell is $r = x$ .

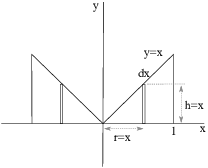
$$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cylindrical-shells-8.eps}}$$

The volume of the solid is

$$V = \int 2 \pi x \cdot x\,dx = 2 \pi\left[\dfrac{1}{3} x^3\right]_0^1 = \dfrac{2 \pi}{3} = 2.09439 \ldots.$$

Note that the thickness of a typical shell is $dx$ , while the thickness of a typical washer is $dy$ .

Example. Let R be the region bounded by $y = x^2$ and $y = 1$ , from $x = 0$ to $x = 1$ .

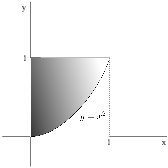
$$\hbox{\epsfysize=1.5in \epsffile{volumes-by-cylindrical-shells-9.eps}}$$

(a) Find the volume generated by revolving R about the line $x = 2$ .

(b) Find the volume generated by revolving R about the line $x = -5$ .

(c) Find the volume generated by revolving R about the line $y = -2$ .

(d) Find the volume generated by revolving R about the line $y = 2$ .

(a) The height of a typical cylindrical shell is $h = 1 - x^2$ . The radius of a typical cylindrical shell is $r = 2 - x$ .

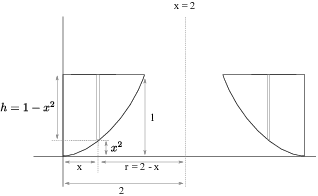
$$\hbox{\epsfysize=1.75in \epsffile{volumes-by-cylindrical-shells-10.eps}}$$

The radius is the distance from the axis to the side of a typical shell. In this case, I found it by subtraction.

Notice that I'm not trying to draw the cross-sectional picture to scale. Also, when I figure out r and h, I do my work on the original copy of the region, not the rotated copy. The rotated copy just gives me a sense of what the volume of revolution looks like.

The volume of the solid is

$$V = \int_0^1 2 \pi (2 - x)(1 - x^2)\,dx = 2 \pi \int_0^1 (2 - x - 2 x^2 + x^3)\,dx = 2 \pi \left[2 x - \dfrac{1}{2}x^2 - \dfrac{2}{3}x^3 + \dfrac{1}{4}x^4\right]_0^1 =$$

$$\dfrac{13 \pi}{6} = 6.80678 \ldots.\quad\halmos$$

(b) The height of a typical cylindrical shell is $h = 1 - x^2$ . The radius of a typical cylindrical shell is $r = 5 + x$ .

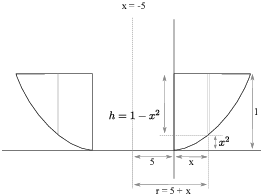
$$\hbox{\epsfysize=1.75in \epsffile{volumes-by-cylindrical-shells-11.eps}}$$

The radius is the distance from the axis to the side of a typical shell. In this case, I found it by addition. (Compare this to what I did in part (a).)

Once again, the picture is not drawn to scale.

The volume of the solid is

$$V = \int_0^1 2 \pi (5 + x)(1 - x^2)\,dx = 2 \pi \int_0^1 (5 + x - 5 x^2 - x^3)\,dx = 2 \pi \left[5 x + \dfrac{1}{2}x^2 - \dfrac{5}{3}x^3 - \dfrac{1}{4}x^4\right]_0^1 =$$

$$\dfrac{43 \pi}{6} = 22.51474 \ldots.\quad\halmos$$

(c) If I solve $y = x^2$ for x, I get $x = \sqrt{y}$ . I use the positive square root, because I'm considering the part of the curve in the first quadrant where x is positive.

The height of a typical cylindrical shell is $h = \sqrt{y}$ . The radius of a typical cylindrical shell is $r = y + 2$ .

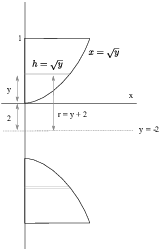
$$\hbox{\epsfysize=2.25in \epsffile{volumes-by-cylindrical-shells-12.eps}}$$

The volume of the solid is

$$V = \int_0^1 2 \pi (y + 2) \sqrt{y}\,dy = 2 \pi \int_0^1 (y^{3/2} + 2 y^{1/2})\,dy = 2 \pi \left[\dfrac{2}{5} y^{5/2} + \dfrac{4}{3} y^{3/2}\right]_0^1 = \dfrac{52 \pi}{15} = 10.89085 \ldots.\quad\halmos$$

You might try to set this problem up using circular washers.

(d) The height of a typical cylindrical shell is $h = \sqrt{y}$ . The radius of a typical cylindrical shell is $r = 2 - y$ .

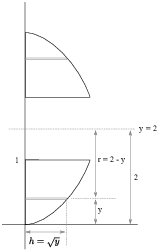
$$\hbox{\epsfysize=2.25in \epsffile{volumes-by-cylindrical-shells-13.eps}}$$

The volume of the solid is

$$V = \int_0^1 2 \pi (2 - y) \sqrt{y}\,dy = 2 \pi \int_0^1 (2 y^{1/2} - y^{3/2})\,dy = 2 \pi \left[\dfrac{4}{3} y^{3/2} - \dfrac{2}{5} y^{5/2}\right]_0^1 = \dfrac{28 \pi}{15} = 5.86430 \ldots.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga