Volumes of Revolution by Washers

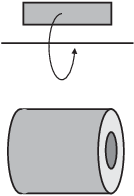
We saw that we could compute a volume of revolution by dividing the volume up into circular slices. However, this method only works if the axis of revolution lies along one edge of the area. If it does not, the volume of revolution may have a "hole" in the middle:

$$\hbox{\epsfysize=1.75in \epsffile{volumes-by-washers-1.eps}}$$

If I cut such a volume into slices, I get circular rings or washers:

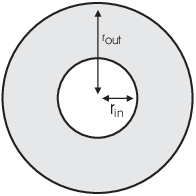
$$\hbox{\epsfysize=1.75in \epsffile{volumes-by-washers-2.eps}}$$

The area of a washer is the area of the outer circle minus the area of the inner circle:

$$\pi r_{\rm out}^2 - \pi r_{\rm in}^2 = \pi(r_{\rm out}^2 - r_{\rm in}^2).$$

Thus, the volume of a typical washer is

$$\pi(r_{\rm out}^2 - r_{\rm in}^2)\cdot (\hbox{thickness}).$$

You can see that this amounts to doing two volumes by circular slices (as above), then subtracting one from the other.

As before, I integrate to find the total volume:

$$V = \int_a^b \pi(r_{\rm out}^2 - r_{\rm in}^2) \cdot (\hbox{thickness}).$$

Example. The region bounded by $y = x^2$ and $y = 1$ is revolved about the x-axis. Find the volume of the solid that is generated.

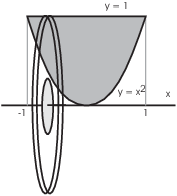
$$\hbox{\epsfysize=1.75in \epsffile{volumes-by-washers-3.eps}}$$

For a typical washer, the inner radius is $r_{\rm in} = x^2$ and the outer radius is $r_{\rm out} = 1$ . You can see this in the picture above, where I've superimposed a typical washer on top of the picture of the region.

The region extends from $x = -1$ to $x = 1$ . The volume is

$$V = \int_{-1}^1 \pi(1^2 - (x^2)^2)\,dx = \pi \int_{-1}^1 (1 - x^4)\,dx = \pi\left[x - \dfrac{1}{5}x^5\right]_{-1}^1 = \dfrac{8 \pi}{5} = 5.02654 \ldots.\quad\halmos$$

Example. The region bounded by $x = y^2$ and $x = 2 - y$ is revolved about the y-axis. Find the volume generated.

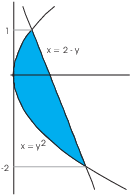
$$\hbox{\epsfysize=1.75in \epsffile{volumes-by-washers-4.eps}}$$

The curves intersect at $y = -2$ and at $y = 1$ . The inner radius is $r_{\rm in} = y^2$ and the outer radius is $r_{\rm out} = 2 - y$ . Notice that the thickness of a typical washer is $dy$ , since it lies in the vertical direction.

The volume of the solid is

$$V = \int_{-2}^1 \pi\left((2 - y)^2 - (y^2)^2\right)\,dy = \pi\left[-\dfrac{1}{3}(2 - y)^3 - \dfrac{1}{5}y^5\right]_{-2}^1 = \dfrac{72 \pi}{5} = 45.23893 \ldots.\quad\halmos$$

Washers are used when the volume of revolution has a "hole" or "gap" in the middle. Another way to handle this is to divide the volume up into cylindrical shells.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga