Work

In this section, we'll see how to compute the work done in various situations: Lifting a weight, pumping water, and compressing or extending a spring. For these examples, you can think of "work" in the everyday sense, since our concern is in showing how to use integration to set up the problems. You can learn about work and related concepts like energy in a physics course.

I will do the examples somewhat informally: I won't write out the Riemann sums, but simply use infinitesimal shorthand and then set up the integrals.

The work required to raise a weight of P pounds a distance of y feet is $P \cdot y$ foot-pounds. (In m-k-s units, one would say that a force of k newtons exerted over a distance of y feet does $k\cdot y$ newton-meters, or joules, of work.)

As an easy example, if a 100 pound weight is lifted a distance of 3 feet, the work done is

$100 \cdot 3 = 300\ \hbox{foot-pounds}.$

Example. A 6-foot cable weighing 0.6 pounds per foot is suspended by one end from a reel. How much work is done in winding the entire cable onto the reel?

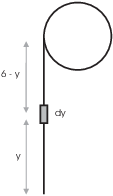
$\hbox{\epsfysize=1.75in \epsffile{work-1.eps}}$

Consider a small piece of the cable of length which is y units above the bottom end (before the cable is wound up). The weight of the piece is $0.6\,dy$ , and it must be raised a distance of feet to get to the reel. The work done in lifting this piece is $(6 - y)(0.6\,dy)$ .

The total work required is

$\int_0^6 (6 - y)(0.6\,dy) = 0.6\left[6y - \dfrac{1}{2}y^2\right]_0^6 = 10.8\ \hbox{foot-pounds}.\quad\halmos$

Example. Find the work done in pumping all the water out of the top of a filled cylindrical tank of radius 3 feet and height 6 feet.

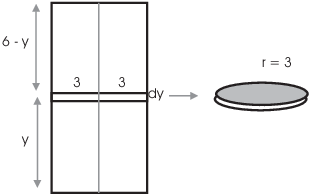
$\hbox{\epsfysize=1.75in \epsffile{work-2.eps}}$

The picture on the left shows a side view of the cylinder. I'll cut the cylinder of water up into circular slices; a typical slice is shown on the right.

I'll make the simplifying assumption that to pump the water in the slice out of the tank, I just need to raise the whole slice vertically to the top of the tank.

Water has a density of 62.4 pounds per cubic foot. A typical circular slice of the water weighs

$62.4 \cdot \pi \cdot 3^2\cdot dy = 9 \pi (62.4)\,dy \quad {\rm pounds}.$

It is raised a distance of feet.

The work done in raising such a slice is $9 \pi (62.4)(6 - y)\,dy$ foot-pounds. Thus, the total work done in emptying the tank is

$W = \int_0^6 9 \pi (62.4) (6 - y)\,dy = 561.6 \pi \left[6 y - \dfrac{1}{2} y^2\right]_0^6 = 581.6 \pi \cdot 18 = 31757.73181 \ldots\ \hbox{foot-pounds}.\quad\halmos$

Example. Find the work done in pumping all the water out of a filled sphere of radius 2 feet. Assume that the water is pumped out of the top of the sphere.

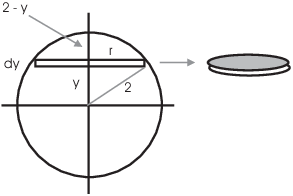
$\hbox{\epsfysize=1.75in \epsffile{work-3.eps}}$

The picture on the left shows a side view of the sphere. I'll cut the cylinder of water up into circular slices; a typical slice is shown on the right.

I'll make the simplifying assumption that to pump the water in the slice out of the tank, I just need to raise the whole slice vertically to the top of the tank.

In the picture, the slice has radius $r = \sqrt{4 - y^2}$ . The weight of the slice is

$62.4 \cdot \pi \cdot (\sqrt{4 - y^2})^2\,dy = 62.4 \pi (4 - y^2)\,dy.$

The slice is raised a distance of feet, so the work done is

$62.4 \pi (4 - y^2)(2 - y)\,dy.$

The total work done is

$W = \int_{-2}^2 62.4 \pi (4 - y^2)(2 - y)\,dy = 62.4 \pi \int_{-2}^2 (8 - 4 y - 2 y^2 + y^3)\,dy = 62.4 \pi \left[8 y - 2 y^2 - \dfrac{2}{3} y^3 + \dfrac{1}{4} y^4\right]_{-2}^2 =$

$62.4 \pi \cdot \dfrac{64}{3} = 4182.08814 \ldots\ \hbox{foot-pounds}.\quad\halmos$

Consider a spring attached at one end to a stationary object, such as a wall. Stretch the spring so that its free end moves a distance x from its unstretched position. The force exerted by the spring is given by Hooke's law:

k is the spring constant; it reflects how difficult it is to stretch the spring. The negative sign reflects the fact that the force is a restoring force: It always points toward the origin.

To stretch the spring, I must exert a force equal to and opposite in direction to the force exerted by the spring: . Suppose I do so, and the end of the spring is moved by a small amount . Then the work done is $F\,dx = k x\,dx$ . Hence, the total work done in stretching the spring from to is

$W = \int_a^b k x\,dx = \left[\dfrac{1}{2} k x^2\right]_a^b = \dfrac{1}{2} k a^2 - \dfrac{1}{2} k b^2.$

Example. A force of 12 pounds is required to stretch a spring 1.5 feet beyond its unstretched length.

(a) What is the spring constant for this spring?

(b) How much work is done in stretching the spring from 2 feet beyond its unstretched length to 4 feet beyond its unstretched length?

(a) Using , I have

$12 = 1.5k, \quad\hbox{so}\quad k = \dfrac{12}{1.5} = 8\ \hbox{pounds per foot}.\quad\halmos$

(b) The work done in stretching the spring by an additional length is $8 x\,dx$ . So the total work is

$W = \int_2^4 8 x\,dx = \left[4 x^2\right]_2^4 = 64 - 16 = 48\ \hbox{foot-pounds}.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page