Inner Product Spaces

Definition. Let V be a vector space over F, where $F = \real$ or $\complex$ . An inner product on V is a function $\innp{\cdot}{\cdot}: V \times V \rightarrow F$ which satisfies:

(a) (Linearity) $\innp{ax + y}{z} = a \innp{x}{z} + \innp{y}{z}$ , for $x, y, z \in V$ , $a \in F$ .

(b) (Symmetry) $\innp{x}{y} = \overline{\innp{y}{x}}$ ,for $x, y \in V$ . ("$\overline x$ " denotes the complex conjugate of x.)

(c) (Positive-definiteness) If $x \ne 0$ , then $\innp{x}{x} \in \real$ and $\innp{x}{x} > 0$ .

A vector space with an inner product is an inner product space. If $F = \real$ , V is a real inner product space; if $F = \complex$ , V is a complex inner product space.

Notation. There are various notations for inner products. You may see "$(x, y)$ " or "$(x \mid y)$ " or "$\left\langle x \mid y \right\rangle$ ", for instance. Some specific inner products come with established notation. For example, the dot product, which I'll discuss below, is denoted "$x \cdot y$ ".

Proposition. Let V be an inner product space over F, where $F = \real$ or $\complex$ . Let $x, y, z \in V$ , and let $a \in F$ .

(a) $\innp{x}{\vec{0}} = 0$ and $\innp{\vec{0}}{x} = 0$ .

(b) $\innp{x}{a y + z} = \overline{a} \innp{x}{y} + \innp{x}{z}$ .

In particular, if $a \in \real$ , then $\innp{x}{a y + z} = a \innp{x}{y} + \innp{x}{z}$ .

(c) If $F = \real$ , then $\innp{x}{y} = \innp{y}{x}$ .

(a)

$$\innp{\vec{0}}{x} = \innp{\vec{0} + \vec{0}}{x} = \innp{\vec{0}}{x} + \innp{\vec{0}}{x}, \quad\hbox{so}\quad 0 = \innp{\vec{0}}{x}.$$

By symmetry, $\innp{x}{\vec{0}} = 0$ as well.

(b)

$$\innp{x}{a y + z} = \overline{\innp{a y + z}{x}} = \overline{a \innp{y}{x} + \innp{z}{x}} = \overline{a} \overline{\innp{y}{x}} + \overline{\innp{z}{x}} = \overline{a} \innp{x}{y} + \innp{x}{z}.$$

If $a \in \real$ , then $\overline{a} = a$ , and so $\innp{x}{a y + z} = a \innp{x}{y} + \innp{x}{z}$ .

(c) As in the proof of (b), I have $\overline{\innp{y}{x}} = \innp{y}{x}$ , so

$$\innp{x}{y} = \overline{\innp{y}{x}} = \innp{y}{x}.\quad\halmos$$

Remarks. Why include complex conjugation in the symmetry axiom? Suppose the symmetry axiom had read

$$\innp{x}{y} = \innp{y}{x}.$$

Then

$$0 < \innp{i x}{i x} = i\innp{x}{i x} = i \innp{i x}{x} = i \cdot i \innp{x}{x} = -\innp{x}{x}.$$

This contradicts $\innp{x}{x} > 0$ . That is, I can't have both pure symmetry and positive definiteness.

Example. Suppose u, v, and w are vectors in a real inner product space V. Suppose

$$\innp{u}{v} = 5, \quad \innp{v}{w} = -2, \quad \innp{u}{w} = 6,$$

$$\innp{v}{v} = 4, \quad \innp{w}{w} = 3.$$

(a) Compute $\innp{u + 3 w}{v - 5 w}$ .

(b) Compute $\innp{v + w}{v - w}$ .

(a) Using the linearity and symmetry properties, I have

$$\innp{u + 3 w}{v - 5 w} = \innp{u}{v - 5 w} + \innp{3 w}{v - 5 w} = \innp{u}{v} - \innp{u}{5 w} + \innp{3 w}{v} - \innp{3 w}{5 w} =$$

$$\innp{u}{v} - 5 \innp{u}{w} + \innp{w}{v} - 15 \innp{w}{w} = 5 - 5 \cdot 6 + (-2) - 15 \cdot 3 = -72.$$

Notice that this "looks like" the polynomial multiplication you learned in basic algebra:

$$(x + 3 z)(y - 5 z) = x y - 5 x z + 3 z y - 15 z^2.$$

(b)

$$\innp{v + w}{v - w} = \innp{v}{v} - \innp{v}{w} + \innp{w}{v} - \innp{w}{w} = \innp{v}{v} - \innp{w}{w} = 4 - 3 = 1.\quad\halmos$$

Example. Let $(a_1, \ldots, a_n), (b_1, \ldots, b_n) \in \real^n$ . The dot product on $\real^n$ is given by

$$(a_1, \ldots, a_n) \cdot (b_1, \ldots, b_n) = a_1 b_1 + \cdots + a_n b_n.$$

It's easy to verify that the axioms for an inner product hold. For example, suppose $(a_1, \ldots, a_n) \ne \vec{0}$ . Then at least one of $a_1$ , ..., $a_n$ is nonzero, so

$$(a_1, \ldots, a_n) \cdot (a_1, \ldots, a_n) = a_1^2 + \cdot + a_n^2 > 0.$$

This proves that the dot product is positive-definite.

I can use an inner product to define lengths and angles. Thus, an inner product introduces (metric) geometry into vector spaces.

Definition. Let V be an inner product space, and let $x, y \in V$ .

(a) The length of x is $\|x\| = \innp{x}{x}^{1/2}$ .

(b) The distance between x and y is $\|x - y\|$ .

(c) The angle between x and y is the smallest positive real number $\theta$ satisfying

$$\cos \theta = \dfrac{\innp{x}{y}}{\|x\| \|y\|}.$$

Remark. The definition of the angle between x and y wouldn't make sense if the expression $\dfrac{\innp{x}{y}}{\|x\| \|y\|}$ was greater than 1 or less than -1, since I'm asserting that it's the cosine of an angle.

In fact, the Cauchy-Schwarz inequality (which I'll prove below) will show that

$$-1 \le \dfrac{\innp{x}{y}}{\|x\| \|y\|} \le 1.\quad\halmos$$

Proposition. Let V be a real inner product space, $a \in \real$ , $x, y \in V$ .

(a) $\|x\|^2 = \innp{x}{x}$ .

(b) $\|a x\| = |a| \|x\|$ . ("$|a|$ " denotes the absolute value of a.)

(c) $x \ne 0$ if and only if $\|x\| > 0$ .

(d) ( Cauchy- Schwarz inequality) $|\innp{x}{y}| \le \|x\|\|y\|$ .

(e) ( Triangle inequality) $\|x + y\| \le \|x\| + \|y\|$ .

Proof. (a) Squaring $\|x\| = \innp{x}{x}^{1/2}$ gives $\|x\|^2 = \innp{x}{x}$ .

(b) Since $\innp{a x}{a x} = a^2 \innp{x}{x}$ ,

$$\|a x\| = \sqrt{a^2} \|x\| = |a|\|x\|.$$

(c) $x \ne 0$ implies $\innp{x}{x} > 0$ , and hence $\|x\| > 0$ . Conversely, if $x = 0$ , then $\innp{0}{0} = 0$ , so $\|x\| = 0$ .

(d) If $x = \vec{0}$ , then

$$|\innp{x}{y}| = |\innp{\vec{0}}{y}| = |0| = 0 \quad\hbox{and}\quad \|\vec{0}\| |\|y\| = 0 \cdot \|y\| = 0.$$

Hence, $|\innp{x}{y}| \le \|x\|\|y\|$ . The same is true if $y = \vec{0}$ .

Thus, I may assume that $x \ne \vec{0}$ and $y \ne \vec{0}$ .

The major part of the proof comes next, and it involves a trick. Don't feel bad if you wouldn't have thought of this yourself: Try to follow along and understand the steps.

If $a, b \in \real$ , then by positive-definiteness and linearity,

$$0 \le \innp{a x - b y}{a x - b y} = a^2 \innp{x}{x} - 2 a b \innp{x}{y} + b^2 \innp{y}{y} = a^2 \|x\|^2 - 2 a b \innp{x}{y} + b^2 \|y\|^2.$$

The trick is to pick "nice" values for a and b. I will set $a = \|y\|$ and $b = \|x\|$ . (A rationale for this is that I want the expression $\|x\| \|y\|$ to appear in the inequality.)

I get

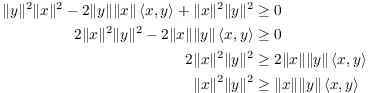
$$\eqalign{ \|y\|^2 \|x\|^2 - 2 \|y\| \|x\| \innp{x}{y} + \|x\|^2 \|y\|^2 & \ge 0 \cr 2 \|x\|^2 \|y\|^2 - 2 \|x\| \|y\| \innp{x}{y} & \ge 0 \cr 2 \|x\|^2 \|y\|^2 & \ge 2 \|x\| \|y\| \innp{x}{y} \cr \|x\|^2 \|y\|^2 & \ge \|x\| \|y\| \innp{x}{y} \cr}$$

Since $x \ne \vec{0}$ and $y \ne \vec{0}$ , I have $\|x\| \ne 0$ and $\|y\| \ne 0$ . So I can divide the inequality by $\|x\| \|y\|$ to obtain

$$\|x\| \|y\| \ge \innp{x}{y}.$$

In the last inequality, x and y are arbitrary vectors. So the inequality is still true if x is replaced by $-x$ . If I replace x with $-x$ , then $\|-x\| = \|x\|$ and $\innp{-x}{y} = - \innp{x}{y}$ , and the inequality becomes

$$\|x\| \|y\| \ge -\innp{x}{y}.$$

Since $\|x\| \|y\|$ is greater than or equal to both $\innp{x}{y}$ and $-\innp{x}{y}$ , I have

$$\|x\|\|y\| \ge |\innp{x}{y}|.$$

(e)

$$\|x + y\|^2 = \innp{x + y}{x + y} = \|x\|^2 + 2 \innp{x}{y} + \|y\|^2 \le \|x\|^2 + 2 \|x\| \|y\| + \|y\|^2 = (\|x\| + \|y\|)^2.$$

Hence, $\|x + y\| \le \|x\| + \|y\|$ .

Example. $\real^3$ is an inner product space using the standard dot product of vectors. The cosine of the angle between $(2, -2, 1)$ and $(6, -8, 24)$ is

$$\cos \theta = \dfrac{(2, -2, 1) \cdot (6, -8, 24)} {\|(2, -2, 1)\| \|(6, -8, 24)\|} = \dfrac{12 + 16 + 24}{(3)(26)} = \dfrac{2}{3}.\quad\halmos$$

Example. Let $C[0, 1]$ denote the real vector space of continuous functions on the interval $[0, 1]$ . Define an inner product on $C[0, 1]$ by

$$\innp{f}{g} = \int_0^1 f(x) g(x)\,dx.$$

Note that $f(x) g(x)$ is integrable, since it's continuous on a closed interval.

The verification that this gives an inner product relies on standard properties of Riemann integrals. For example, if $f \ne 0$ ,

$$\innp{f}{f} = \int_0^1 f(x)^2\,dx > 0.$$

Given that this is a real inner product, I may apply the preceding proposition to produce some useful results. For example, the Cauchy-Schwarz inequality says that

$$\left(\int_0^1 f(x)^2\,dx\right)^{1/2} \left(\int_0^1 g(x)^2\,dx\right)^{1/2} \ge \left|\int_0^1 f(x) g(x)\,dx\right|.\quad\halmos$$

Definition. A set of vectors S in an inner product space V is orthogonal if $\innp{v_i}{v_j} = 0$ for $v_i, v_j \in S$ , $v_i \ne v_j$ .

An orthogonal set S is orthonormal if $\|v_i\| = 1$ for all $v_i \in S$ .

If you've seen dot products in a multivariable calculus course, you know that vectors in $\real^n$ whose dot product is 0 are perpendicular. With this interpretation, the vectors in an orthogonal set are mutually perpendicular. The vectors in an orthonormal set are mutually perpendicular unit vectors.

Notation. If I is an index set, the Kronecker delta $\delta_{ij}$ (or $\delta(i,j)$ ) is defined by

$$\delta_{ij} = \cases{0 & if $i \ne j$\cr 1 & if $i = j$\cr}$$

With this notation, a set $S = \{v_i\}$ is orthonormal if

$$\innp{v_i}{v_j} = \delta_{ij}.$$

Note that the $n \times n$ matrix whose $(i, j)$ -th component is $\delta_{ij}$ is the $n \times n$ identity matrix.

Example. The standard basis for $\real^n$ is

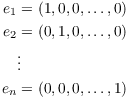
$$\eqalign{ e_1 & = (1, 0, 0, \ldots, 0) \cr e_2 & = (0, 1, 0, \ldots, 0) \cr & \vdots \cr e_n & = (0, 0, 0, \ldots, 1) \cr}$$

It's clear that relative to the dot product on $\real^n$ , each of these vectors as length 1, and each pair of the vectors has dot product 0. Hence, the standard basis is an orthonormal set relative to the dot product on $\real^n$ .

Example. Consider the following set of vectors in $\real^2$ :

$$\left\{ \left(\dfrac{3}{5}, \dfrac{4}{5}\right), \left(-\dfrac{4}{5}, \dfrac{3}{5}\right)\right\}.$$

I have

$$\left(\dfrac{3}{5}, \dfrac{4}{5}\right) \cdot \left(\dfrac{3}{5}, \dfrac{4}{5}\right) = \dfrac{9}{25} + \dfrac{16}{25} = 1,$$

$$\left(\dfrac{3}{5}, \dfrac{4}{5}\right) \cdot \left(-\dfrac{4}{5}, \dfrac{3}{5}\right) = -\dfrac{12}{25} + \dfrac{12}{25} = 0,$$

$$\left(-\dfrac{4}{5}, \dfrac{3}{5}\right) \cdot \left(-\dfrac{4}{5}, \dfrac{3}{5}\right) = \dfrac{16}{25} + \dfrac{9}{25} = 1.$$

It follows that the set is orthonormal relative to the dot product on $\real^2$ .

Example. Let $C[0, 2 \pi]$ denote the complex-valued continuous functions on $[0, 2 \pi]$ . Define an inner product by

$$\innp{f}{g} = \dfrac{1}{2 \pi} \int_0^{2 \pi} f(x) \overline{g(x)}\,dx.$$

Let $m, n \in \integer$ . Then

$$\dfrac{1}{2 \pi} \int_0^{2 \pi} e^{i m x} e^{-i n x}\,dx = \delta_{m n}.$$

It follows that the following set is orthonormal in $C[0, 2 \pi]$ relative to this inner product:

$$\left\{\dfrac{1}{\sqrt{2 \pi}} e^{i m x} \bigm| m = \ldots, -1, 0, 1, \ldots \right\}\quad\halmos$$

Proposition. Let $\{v_i\}$ be an orthogonal set of vectors, $v_i \ne 0$ for all i. Then $\{v_i\}$ is independent.

Proof. Suppose

$$a_1 v_{i_1} + a_2 v_{i_2} + \cdots + a_n v_{i_n} = \vec{0}.$$

Take the inner product of both sides with $v_{i_1}$ :

$$a_1 \innp{v_{i_1}}{v_{i_1}} + a_2 \innp{v_{i_1}}{v_{i_2}} + \cdots + a_n \innp{v_{i_1}}{v_{i_n}} = 0.$$

Since $\{v_i\}$ is orthogonal,

$$\innp{v_{i_1}}{v_{i_2}} = \cdots = \innp{v_{i_1}}{v_{i_n}} = 0.$$

The equation becomes

$$a_1 \innp{v_{i_1}}{v_{i_1}} = 0.$$

But $\innp{v_{i_1}}{v_{i_1}} > 0$ by positive-definiteness, since $v_{i_1} \ne \vec{0}$ . Therefore, $a_1 = 0$ .

Similarly, taking the inner product of both sides of the original equation with $v_{i_2}$ , ... $v_{i_n}$ shows $a_j = 0$ for all j. Therefore, $\{v_i\}$ is independent.

An orthonormal set consists of vectors of length 1, so the vectors are obviously nonzero. Hence, an orthonormal set is independent, and forms a basis for the subspace it spans. A basis which is an orthonormal set is called an orthonormal basis.

It is very easy to find the components of a vector relative to an orthonormal basis.

Proposition. Let $\{v_i\}$ be an orthonormal basis for V, and let $v \in V$ . Then

$$v = \sum_{i} \innp{v}{v_i} v_i.$$

Note: In fact, the sum above is a finite sum --- that is, only finitely many terms are nonzero.

Proof. Since $\{v_i\}$ is a basis, there are elements $a_j \in F$ and $v_{i_v} \in \{v_i\}$ such that

$$v = a_1 v_{i_1} + a_2 v_{i_2} + \cdots + a_n v_{i_n}.$$

Take the inner product of both sides with $v_{i_1}$ . Then

$$\innp{v}{v_{i_1}} = a_1 \innp{v_{i_1}}{v_{i_1}} + a_2 \innp{v_{i_2}}{v_{i_1}} + \cdots + a_n \innp{v_{i_n}}{v_{i_1}}.$$

As in the proof of the last proposition, all the inner product terms on the right vanish, except that $\innp{v_{i_1}}{v_{i_1}} = 1$ by orthonormality. Thus,

$$\innp{v}{v_{i_1}} = a_1.$$

Taking the inner product of both sides of the original equation with $v_{i_2}$ , ... $v_{i_n}$ shows

$$\innp{v}{v_{i_2}} = a_2, \ldots \innp{v}{v_{i_n}} = a_n.\quad\halmos$$

Example. Here is an orthonormal basis for $\real^2$ :

$$\left\{ \left[\matrix{\dfrac{3}{5} \cr \noalign{\vskip2pt} \dfrac{4}{5} \cr}\right], \left[\matrix{-\dfrac{4}{5} \cr \noalign{\vskip2pt} \dfrac{3}{5} \cr}\right]\right\}$$

To express $(-7, 6)$ in terms of this basis, take the dot product of the vector with each element of the basis:

$$(-7, 6) \cdot \left(\dfrac{3}{5}, \dfrac{4}{5}\right) = \dfrac{3}{5},$$

$$(-7, 6) \cdot \left(-\dfrac{4}{5}, \dfrac{3}{5}\right) = \dfrac{46}{5}.$$

Hence,

$$\left[\matrix{-7 \cr 6 \cr}\right] = \dfrac{3}{5} \cdot \left[\matrix{\dfrac{3}{5} \cr \noalign{\vskip2pt} \dfrac{4}{5} \cr}\right] + \dfrac{46}{5} \cdot \left[\matrix{-\dfrac{4}{5} \cr \noalign{\vskip2pt} \dfrac{3}{5} \cr}\right].\quad\halmos$$

Example. Let $C[0, 2 \pi]$ denote the complex inner product space of complex-valued continuous functions on $[0, 2 \pi]$ , where the inner product is defined by

$$\innp{f}{g} = \dfrac{1}{2 \pi} \int_0^{2 \pi} f(x) \overline{g(x)}\,dx.$$

I noted earlier that the following set is orthonormal:

$$S = \left\{\dfrac{1}{\sqrt{2 \pi}} e^{mix} \bigm| m = \ldots, -1, 0, 1, \ldots \right\}.$$

Suppose I try to compute the "components" of $f(x) = x$ relative to this orthonormal set by taking inner products --- that is, using the approach of the preceding example.

For $m = 0$ ,

$$\dfrac{1}{\sqrt{2 \pi}} \int_0^{2 \pi} x\,dx = \pi\sqrt{2 \pi}.$$

Suppose $m \ne 0$ . Then

$$\dfrac{1}{\sqrt{2 \pi}} \int_0^{2 \pi} x e^{-m i x}\,dx = \dfrac{1}{\sqrt{2 \pi}}\left[\dfrac{i}{m} x e^{-m i x} - \dfrac{1}{m^2} e^{-m i x}\right]_0^{2 \pi} = \dfrac{i \sqrt{2 \pi}}{m}.$$

There are infinitely many nonzero components! Of course, the reason this does not contradict the earlier result is that $f(x) = x$ may not lie in the span of S. S is orthonormal, hence independent, but it is not a basis for $C[0, 2 \pi]$ .

In fact, since $e^{m i x} = \cos m x + i \sin m x$ , a finite linear combination of elements of S must be periodic.

It is still reasonable to ask whether (or in what sense) $f(x) = x$ can be represented by the the infinite sum

$$\pi\sqrt{2 \pi} + \sum_{m=1}^\infty \left(\dfrac{i \sqrt{2 \pi}}{m} e^{m i x} - \dfrac{i \sqrt{2 \pi}}{m} e^{-m i x}\right).$$

For example, it is reasonable to ask whether the series converges uniformly to f at each point of $[0, 2 \pi]$ . The answers to these kinds of questions would require an excursion into the theory of Fourier series.

Since it's so easy to find the components of a vector relative to an orthonormal basis, it's of interest to have an algorithm which converts a given basis to an orthonormal one.

The Gram-Schmidt algorithm converts a basis to an orthonormal basis by "straightening out" the vectors one by one.

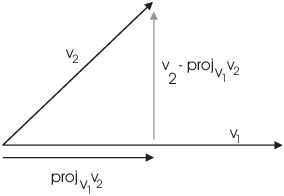
$$\hbox{\epsfysize=1.75in \epsffile{inner-products1.eps}}$$

The picture shows the first step in the straightening process. Given vectors $v_1$ and $v_2$ , I want to replace $v_2$ with a vector perpendicular to $v_1$ . I can do this by taking the component of $v_2$ perpendicular to $v_1$ , which is

$$v_2 - \dfrac{\innp{v_1}{v_2}}{\innp{v_1}{v_1}} v_1.$$

Lemma. ( Gram-Schmidt algorithm) Let $\{v_1, \ldots, v_k\}$ be a set of nonzero vectors in an inner product space V. Suppose $v_1$ , ..., $v_{k-1}$ are pairwise orthogonal. Let

$$v_k' = v_k - \sum_{i=1}^{k-1} \dfrac{\innp{v_i}{v_k}}{\innp{v_i}{v_i}} v_i.$$

Then $v_k'$ is orthogonal to $v_1$ , ..., $v_{k-1}$ .

Proof. Let $j \in \{1, \ldots, k - 1\}$ . Then

$$\innp{v_j}{v_k'} = \innp{v_j}{v_k} - \sum_{i=1}^{k-1} \dfrac{\innp{v_i}{v_k}}{\innp{v_i}{v_i}} \innp{v_j}{v_i}.$$

Now $\innp{v_j}{v_i} = 0$ for $i \ne j$ because the set is orthogonal. Hence, the right side collapses to

$$\innp{v_j}{v_k} - \dfrac{\innp{v_j}{v_k}}{\innp{v_j}{v_j}} \innp{v_j}{v_j} = \innp{v_j}{v_k} - \innp{v_j}{v_k} = 0.\quad\halmos$$

Suppose that I start with an independent set $\{v_1, \ldots, v_n\}$ . Apply the Gram-Schmidt procedure to the set, beginning with $v_1' = v_1$ . This produces an orthogonal set $\{v_1', \ldots, v_n'\}$ . In fact, $\{v_1', \ldots, v_n'\}$ is a nonzero orthogonal set, so it is independent as well.

To see that each $v_k'$ is nonzero, suppose

$$0 = v_k' = v_k - \sum_{i=1}^{k-1} \dfrac{\innp{v_i}{v_k}}{\innp{v_i}{v_i}} v_i.$$

Then

$$v_k = \sum_{i=1}^{k-1} \dfrac{\innp{v_i}{v_k}}{\innp{v_i}{v_i}} v_i.$$

This contradicts the independence of $\{v_i\}$ , because $v_k$ is expressed as the linear combination of $v_1$ , ... $v_{k-1}$ .

In general, if the algorithm is applied iteratively to a set of vectors, the span is preserved at each state. That is,

$$\langle v_1, \ldots, v_k \rangle = \langle v_1', \ldots, v_k' \rangle.$$

This is true at the start, since $v_1 = v_1'$ . Assume inductively that

$$\langle v_1, \ldots, v_{k-1} \rangle = \langle v_1', \ldots, v_{k-1}' \rangle.$$

Consider the equation

$$v_k' = v_k - \sum_{i=1}^{k-1} \dfrac{\innp{v_i}{v_k}}{\innp{v_i}{v_i}} v_i.$$

It expresses $v_k'$ as a linear combination of $\{v_1, \ldots, v_k\}$ . Hence, $\langle v_1', \ldots, v_k' \rangle \subset \langle v_1, \ldots, v_k \rangle$ .

Conversely,

$$v_k = v_k' + \sum_{i=1}^{k-1} \dfrac{\innp{v_i}{v_k}}{\innp{v_i}{v_i}} v_i \subset \langle v_k' \rangle + \langle v_1, \ldots, v_{k-1} \rangle =$$

$$\langle v_k' \rangle + \langle v_1', \ldots, v_{k-1}' \rangle = \langle v_1', \ldots, v_k' \rangle.$$

It follows that $\langle v_1, \ldots, v_k \rangle \subset \langle v_1', \ldots, v_k' \rangle$ , so $\langle v_1, \ldots, v_k \rangle = \langle v_1', \ldots, v_k' \rangle$ , by induction.

To summarize: If you apply Gram-Schmidt to a set of vectors, the algorithm produces a new set of vectors with the same span as the old set. If the original set was independent, the new set is independent (and orthogonal) as well.

So, for example, if Gram-Schmidt is applied to a basis for an inner product space, it will produce an orthogonal basis for the space.

Finally, you can always produce orthonormal set from a orthogonal set (of nonzero vectors) --- merely divide each vector in the orthogonal set by its length.

Example. ( Gram-Schmidt) Apply Gram-Schmidt to the following set of vectors in $\real^3$ (relative to the usual dot product):

$$\left\{\left[\matrix{3 \cr 0 \cr 4 \cr}\right], \left[\matrix{-1 \cr 0 \cr 7 \cr}\right], \left[\matrix{2 \cr 9 \cr 11 \cr}\right]\right\}.$$

$$v_1' = v_1 = (3, 0, 4),$$

$$v_2' = (-1, 0, 7) - \dfrac{(-1, 0, 7) \cdot (3, 0, 4)}{(3, 0, 4) \cdot (3, 0, 4)} (3, 0, 4) = (-4, 0, 3).$$

$$v_3' = (2, 9, 11) - \dfrac{(2, 9, 11) \cdot (3, 0, 4)}{(3, 0, 4) \cdot (3, 0, 4)} (3, 0, 4) - \dfrac{(2, 9, 11) \cdot (-4, 0, 3)}{(-4, 0, 3) \cdot (-4, 0, 3)} (-4, 0, 3) = (0, 9, 0).$$

(A common mistake here is to project onto $v_1$ , $v_2$ , ... . I need to project onto the vectors that have already been orthogonalized. That is why I projected onto $(3, 0, 4)$ and $(-4, 0, 3)$ rather than $(3, 0, 4)$ and $(-1, 0, 7)$ .)

The algorithm has produced the following orthogonal set:

$$\left\{\left[\matrix{3 \cr 0 \cr 4 \cr}\right], \left[\matrix{-4 \cr 0 \cr 3 \cr}\right], \left[\matrix{0 \cr 9 \cr 0 \cr}\right]\right\}.$$

The lengths of these vectors are 5, 5, and 9. For example

$$\|(3, 0, 4)\| = \sqrt{3^2 + 0^2 + 4^2} = 5.$$

The correponding orthonormal set is

$$\left\{\dfrac{1}{5}\left[\matrix{3 \cr 0 \cr 4 \cr}\right], \dfrac{1}{5}\left[\matrix{-4 \cr 0 \cr 3 \cr}\right], \left[\matrix{0 \cr 1 \cr 0 \cr}\right]\right\}.\quad\halmos$$

Example. ( Gram-Schmidt) Find an orthonormal basis (relative to the usual dot product) for the subspace of $\real^4$ spanned by the vectors

$$v_1 = (1, 0, 2, 2), \quad v_2 = (10, 1, 0, 4), \quad v_3 = (1, 1, 0, 13).$$

I'll use $v_1'$ , $v_2'$ , $v_3'$ to denote the orthonormal basis.

To simplify the computations, you should fix the vectors so they're mutually perpendicular first. Then you can divide each by its length to get vectors of length 1.

First,

$$v_1' = v_1 = \langle 1, 0, 2, 2\rangle.$$

Next,

$$v_2' = v_2 - \dfrac{v_2 \cdot v_1'}{v_1' \cdot v_1'} v_1' = (10, 1, 0, 4) - \dfrac{(10, 1, 0, 4)\cdot (1, 0, 2, 2)}{(1, 0, 2, 2)\cdot (1, 0, 2, 2)} (1, 0, 2, 2) =$$

$$(10, 1, 0, 4) - 2 \cdot (1, 0, 2, 2) = (10, 1, 0, 4) - (2, 0, 4, 4) = (8, 1, -4, 0).$$

You can check that $v_2'\cdot v_1' = 0$ , so the first two are perpendicular.

Finally,

$$v_3' = v_3 - \dfrac{v_3\cdot v_1'}{v_1'\cdot v_1'} v_1' - \dfrac{v_3\cdot v_2'}{v_2'\cdot v_2'} v_2' =$$

$$(1, 1, 0, 13) - \dfrac{(1, 1, 0, 13) \cdot (1, 0, 2, 2)} {(1, 0, 2, 2) \cdot (1, 0, 2, 2)} (1, 0, 2, 2) - \dfrac{(1, 1, 0, 13) \cdot (8, 1, -4, 0)} {(8, 1, -4, 0) \cdot (8, 1, -4, 0)} (8, 1, -4, 0) =$$

$$(1, 1, 0, 13) - \dfrac{27}{9} \cdot (1, 0, 2, 2) - \dfrac{9}{81} \cdot (8, 1, -4, 0) = (1, 1, 0, 13) - (3, 0, 6, 6) - \left(\dfrac{8}{9}, \dfrac{1}{9}, -\dfrac{4}{9}, 0\right) =$$

$$\left(-\dfrac{26}{9}, \dfrac{8}{9}, -\dfrac{50}{9}, 7\right).$$

If at any point you wind up with a vector with fractions, it's a good idea to clear the fractions before continuing. Since multiplying a vector by a number doesn't change its direction, it remains perpendicular to the vectors already constructed.

Thus, I'll multiply the last vector by 9 and use

$$v_3' = (-26, 8, -50, 63).$$

Thus, the orthogonal set is

$$v_1' = (1, 0, 2, 2), \quad v_2' = (8, 1, -4, 0), \quad v_3' = (-26, 8, -50, 63).$$

The lengths of these vectors are 3, 9, and $\sqrt{7209} = 9 \sqrt{89}$ . Dividing the vectors by their lengths gives and orthonormal basis:

$$\left(\dfrac{1}{3}, 0, \dfrac{2}{3}, \dfrac{2}{3}\right), \left(\dfrac{8}{9}, \dfrac{1}{9}, -\dfrac{4}{9}, 0\right), \left(-\dfrac{26}{9 \sqrt{89}}, \dfrac{8}{9 \sqrt{89}}, -\dfrac{50}{9 \sqrt{89}}, \dfrac{7}{\sqrt{89}}\right).\quad\halmos$$

Recall that when an n-dimensional vector is interpreted as a matrix, it is taken to be an $n \times 1$ matrix: that is, an n-dimensional column vector

$$(v_1, v_2, \ldots v_n) = \left[\matrix{v_1 \cr v_2 \cr \vdots \cr v_n \cr}\right].$$

If I need an n-dimensional row vector, I'll take the transpose. Thus,

$$(v_1, v_2, \ldots v_n)^T = \left[\matrix{v_1 & v_2 & \cdots & v_n \cr}\right].$$

Lemma. Let A be an invertible $n \times n$ matrix with entries in $\real$ . Let

$$\innp{x}{y} = x^T A^T A y.$$

Then $\innp{}{}$ defines an inner product on $\real^n$ .

Proof. I have to check linearity, symmetry, and positive definiteness.

First, if $a \in \real$ , then

$$\innp{ax_1 + x_2}{y} = (a x_1 + x_2) A^T A y = a (x_1 A^T A y) + x_2 A^T A y = a \innp{x_1}{y} + \innp{x_2}{y}.$$

This proves that the function is linear in the first slot.

Next,

$$\innp{x}{y} = x^T A^T A y = (y^T A^T A x)^T = y^T A^T A x = \innp{y}{x}.$$

The second equality comes from the fact that $(B C)^T = C^T B^T$ for matrices. The third inequality comes from the fact that $y^T A^T A x$ is a $1 \times 1$ matrix, so it equals its transpose.

This proves that the function is symmetric.

Finally,

$$\innp{x}{x} = x^T A^T A x = (A x)^T (A x).$$

Now $A x$ is an $n \times 1$ vector --- I'll label its components this way:

$$A x = \left[\matrix{u_1 \cr u_2 \cr \vdots \cr u_n \cr}\right].$$

Then

$$\innp{x}{x} = (A x)^T (A x) = \left[\matrix{u_1 & u_2 & \cdots & u_n \cr}\right] \left[\matrix{u_1 \cr u_2 \cr \vdots \cr u_n \cr}\right] = u_1^2 + u_2^2 + \cdots + u_n^2 \ge 0.$$

That is, the inner product of a vector with itself is a nonnegative number. All that remains is to show that if the inner product of a vector with itself is 0, them the vector is $\vec{0}$ .

Using the notation above, suppose

$$0 = (x, x) = u_1^2 + u_2^2 + \cdots + u_n^2.$$

Then $u_1 = u_2 = \cdots = u_n = 0$ , because a nonzero u would produce a positive number on the right side of the equation.

So

$$A x = \left[\matrix{u_1 \cr u_2 \cr \vdots \cr u_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right] = \vec{0}.$$

Finally, I'll use the fact that A is invertible:

$$A^{-1} A x = A^{-1} \vec{0}, \quad x = \vec{0}.$$

This proves that the function is positive definite, so it's an inner product.

Example. The previous lemma provides lots of examples of inner products on $\real^n$ besides the usual dot product. All I have to do is take an invertible matrix A and form $A^TA$ , defining the inner product as above.

For example, this $2 \times 2$ real matrix is invertible:

$$A = \left[\matrix{ 5 & 2 \cr 2 & 1 \cr}\right].$$

Now

$$A^T A = \left[\matrix{ 29 & 12 \cr 12 & 5 \cr}\right].$$

(Notice that $A^TA$ will always be symmetric.) The inner product defined by this matrix is

$$\innp{(x_1, x_2)}{y_1, y_2)} = \left[\matrix{x_1 & x_2 \cr}\right] \left[\matrix{ 29 & 12 \cr 12 & 5 \cr}\right] \left[\matrix{y_1 \cr y_2 \cr}\right] = 29 x_1 y_1 + 12 x_2 y_1 + 12 x_1 y_2 + 5 x_2 y_2.$$

For example, under this inner product,

$$\innp{(1, 2)}{(-8, 3)} = -358, \quad\hbox{and}\quad \|(5, -2))\| = \sqrt{505}.\quad\halmos$$

Definition. A matrix A in $M(n,\real)$ is orthogonal if $A A^T = I$ .

Proposition. Let A be an orthogonal matrix.

(a) $\det(A) = \pm 1$ .

(b) $A A^T = I = A^T A$ --- in other words, $A^T = A^{-1}$ .

(c) The rows of A form an orthonormal set. The columns of A form an orthonormal set.

(d) A preserves dot products --- and hence, lengths and angles --- in the sense that

$$(A x) \cdot (A y) = x \cdot y.$$

Proof. (a) If A is orthogonal,

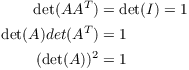
$$\eqalign{ \det(A A^T) & = \det(I) = 1 \cr \det(A) det(A^T) & = 1 \cr (\det(A))^2 & = 1 \cr}$$

Therefore, $\det(A) = \pm 1$ .

(b) Since $\det A = \pm 1$ , the determinant is certainly nonzero, so A is invertible. Hence,

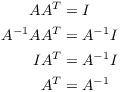
$$\eqalign{ A A^T & = I \cr A^{-1} A A^T & = A^{-1} I \cr I A^T & = A^{-1} I \cr A^T & = A^{-1} \cr}$$

But $A^{-1} A = I$ , so $A^T A= I$ as well.

(c) The equation $A A^T = I$ implies that the rows of A form an orthonormal set of vector. Likewise, $A^T A = I$ shows that the same is true for the columns of A.

(d) The ordinary dot product of vectors $x = (x_1, x_2, \ldots x_n)$ and $y = (y_1, y_2, \ldots y_n)$ can be written as a matrix multiplication:

$$x \cdot y = \left[\matrix{x_1 & x_2 & \cdots & x_n \cr}\right] \left[\matrix{y_1 \cr y_2 \cr \vdots \cr y_n \cr}\right] = x^T y.$$

(Remember the convention that vectors are column vectors.)

Suppose A is orthogonal. Then

$$(A x) \cdot (A y) = (A x)^T (A y) = x^T A^T A y = x^T I y = x^T y = x \cdot y.$$

In other words, orthogonal matrices preserve dot products. It follows that orthogonal matrices will also preserve lengths of vectors and angles between vectors, because these are defined in terms of dot products.

Example. Find real numbers a and b such that the following matrix is orthogonal:

$$A = \left[\matrix{ a & 0.6 \cr b & 0.8 \cr}\right].$$

Since the columns of A must form an orthonormal set, I must have

$$(a, b) \cdot (0.6, 0.8) = 0 \quad\hbox{and}\quad \|(a, b)\| = 1.$$

(Note that $\|(0.6, 0.8)\| = 1$ already.) The first equation gives

$$0.6 a + 0.8 b = 0.$$

The easy way to get a solution is to swap 0.6 and 0.8 and negate one of them; thus, $a = -0.8$ and $b = 0.6$ .

Since $\|(-0.8, 0.6)\| = 1$ , I'm done. (If the a and b I chose had made $\|(a, b)\| \ne 1$ , then I'd simply divide $(a, b)$ by its length.)

Example. Orthogonal $2 \times 2$ matrices represent rotations of the plane about the origin or reflections across a line through the origin.

Rotations are represented by matrices

$$\left[\matrix{ \cos \theta & -\sin \theta \cr \sin \theta & \cos \theta \cr}\right].$$

You can check that this works by considering the effect of multiplying the standard basis vectors $(1, 0)$ and $(0, 1)$ by this matrix.

Multiplying a vector by the following matrix product reflects the vector across the line L that makes an angle $\theta$ with the x-axis:

$$\left[\matrix{ \cos \theta & -\sin \theta \cr \sin \theta & \cos \theta \cr}\right] \left[\matrix{ 1 & 0 \cr 0 & -1 \cr}\right] \left[\matrix{ \cos \theta & \sin \theta \cr -\sin \theta & \cos \theta \cr}\right].$$

Reading from right to left, the first matrix rotates everything by $-\theta$ radians, so L coincides with the x-axis. The second matrix reflects everything across the x-axis. The third matrix rotates everything by $\theta$ radians. Hence, a given vector is rotated by $-\theta$ and reflected across the x-axis, after which the reflected vector is rotated by $\theta$ . The net effect is to reflect across L.

Many transformation problems can be easily accomplished by doing transformations to reduce a general problem to a special case.

Send comments about this page to: Bruce.Ikenaga@millersville.edu.

Bruce Ikenaga's Home Page

Copyright 2014 by Bruce Ikenaga